机器学习——概率论的加和与乘积规则

下面来推导概率论的加和与乘法规则
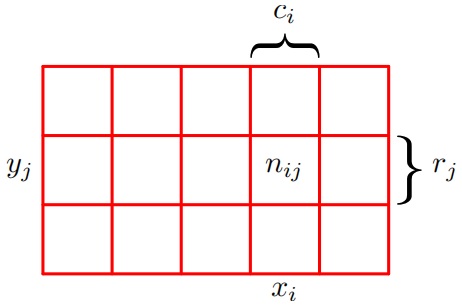
  假设两个随机变量X和Y，随机变量X可以随机取任意的\(x_i, i=1,2,..., M\)，随机变量Y可以随机取任意的\(y_j,j=1,2,...,L\)。进行N次试验，对X和Y都进行了取样，把\(X=x_i\)且\(Y=y_i\)出现的试验次数记为\(n_{ij}\)。并且把X取值为\(x_i\)（与Y的取值无关）出现的试验次数记为\(c_i\), 类似地，把Y取值为\(y_j\)的试验数量的次数记为\(r_j\)。
  X取值为\(x_i\)且Y取值为\(y_j\)的概率记为\(p(X=x_i,Y=y_j)\),被称为\(X=x_i\)和\(Y=y_i\)的联合概率（joint probability）。它的计算方法为落在单元格i,j的点的数量与总的点数的比值，即
      \(p(X=x_i,Y=y_j)=\frac{n_{ij}}{N}\)      (1.5)
类似地，X取值\(x_i\)的概率被记为\(p(X=x_i)\)，它的计算方法为落在第i列上点数与点的总数的比值，即
      \(p(X=x_i)=\frac{c_i}{N}\)      (1.6)
Y取\(y_j\)的概率记为\(p(Y=y_j)\), 它的计算方法为落在第j行的点数与点的总数的比值，即\(p(Y=y_j)=\frac{r_j}{N}\)
由于下面图片中第i列各个方格里面点数之和满足\(c_i=\sum_{j}{n_{ij}}\),因此可以可以推导
      \(p(X=x_i)=\frac{c_i}{N}=\frac{\sum_{j}{n_{ij}}}{N}=\sum_{j}{\frac{n_{ij}}{N}}=\sum_j{p(X=x_i,Y=y_j)}\)   (1.7)
公式（1.7）就是概率的加和规则。注意，此次单个变量的概率\(p(X=x_i)\)有时被称为边缘概率。如果我们只考虑那些\(X=x_i\)的实例，那么这些实例中\(Y=y_j\)的实例所占的比例被写成\(p(Y=y_j|X=x_i)\)，被称为给定\(X=x_i\)的\(Y=y_j\)的条件概率（conditional probability）。它的计算方式为：计算落在单元格\(ij\)的点的数量与第i列的点的数量的比值，即
      \(p(Y=y_j|X=x_i)=\frac{n_{ij}}{c_j}\)       (1.8)
根据公式（1.5）（1.6）（1.8），可以推导出下面公式
      \(p(X=x_i,Y=y_j)=\frac{n_{ij}}{N}=\frac{n_{ij}}{c_i}*\frac{c_{i}}{N}=p(Y=y_j|X=x_i)p(X=x_i)\) (1.9)
这个就是概率论的乘法规则。

  使用如下简单的记法来表示概率论的两条基本规则：
    sum rule \(p(X)=\sum_Y{p(X,Y)}\)    (1.10)
    product rule \(p(X,Y)=p(Y|X)p(X)\)    (1.11)
这里的\(p(X,Y)\)是联合概率，可以表述为“X且Y的概率”。类似地，\(p(Y|X)\)是条件概率，可以表述为“给定X条件下Y的概率”，\(p(X)\)是边缘概率，可以表述为“X的概率”。这两个简单的规则是概率论的基础。

  上面介绍了概率论的两个重要的规则：加和规则和乘法规则。涉及到联合概率、条件概率、边缘概率这些名词和概念。下面基于此引入贝叶斯定理。由于联合概率的定义可知\(p(X,Y)=p(Y,X)\)，根据乘法规则\(p(X,Y)=p(Y|X)p(X)=p(X|Y)p(Y)\)，可以推导出
      \(p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)}\)      （1.12）
这就是贝叶斯定理，在模式识别和机器学校领域中扮演者中心角色。使用（1.10）（1.11）可以得到\(p(X)=\sum_Y{p(X|Y)}{p(Y)}\)，由此可见分母可以用出现在分子中的项来表示。我们可以将分母看出一个归一化的常数，用于确保公式（1.12）左侧的条件概率对于所有的取Y值之和为1

参考
【1】机器学习 周志华