Data Management Technology(2) -- Data Model

1.Data Model

Model

• Is the abstraction of real world
• Reveal the essence of objects, help people to locate and resolve problems

Data Model

• A data model explicitly determines the structure of data, and defines the operation that can be imposed, in order to represent the characteristic of the world
• Data model is the core and fundamental of database
  • Data model determines the function and performance of database
• There exists different data models
  • From different level, or different point of view
  • The evolution of data model promotes the database progress
• Conceptual model
  • documents and organizes the data for communication between functional and technical people
• Logical model
  • describes data semantics, data relationships, data constraints and data operation in database
• Physical model
  • describes how data is organized in storage device

Different level of abstraction

 

 

 

 

 

Real World

概念模型 Conceptual Mode

逻辑模型 Logical Model

物理模型 Physical Model

Computer

2.Conceptual Model - ER Model

• Is the most popular conceptual model
• Gives us a language to specify
  • what information the db must hold
  • what are the relationships among components of that information
• View the world as a collection of entities

 

 

 

 

Ideas

E/R design

Relational schema

Relational DBMS

Basic stuff

Entities and Attributes

（1）Entities

• real-world objects distinguishable from other objects
• described using a set of attributes
• Example: specific person, company, event, plant

（2）Attributes属性

• each has an atomic domain: string, integers, reals, etc.
• An entity is represented by a set of attributes, that is descriptive properties
  possessed by all members of an entity set.
• Domain – the set of permitted values for each attribute. Value types: Integer, String, Real,… etc.
• Attribute types:
  • Simple and composite attributes.
  • Single-valued and multi-valued attributes
    • Example: multivalued attribute: phone_numbers
  • Derived attributes
    • Can be computed from other attributes
    • Example: age, given date_of_birth

（3）Entity set

• a collection of similar entities
• Example: set of all persons, companies, trees, holidays

Relations

A mathematical definition: –if A, B are sets, then a relation R is a subset of A × B

The degree of relationship

• Binary relationship
• Ternary relationship
• Unitary relationship

Relationship Attribute

• An attribute can also be property of a relationship.
• Modeled as a mathematical set
• Binary and multiway relationships
• Converting a multiway one into many binary ones
• Constraints on the degree of the relationship
• many-one, one-one, many-many
• Attributes of relationships
• not necessary, but useful

Multiway Relationships

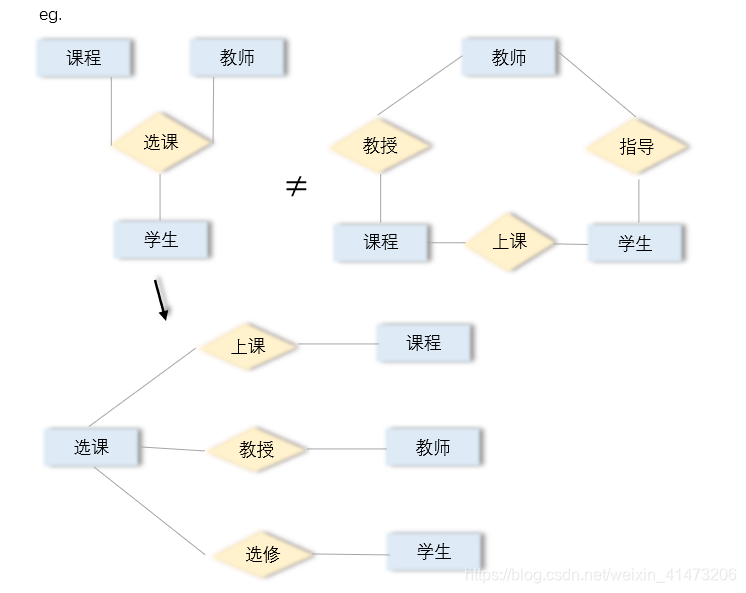左：只有一个关系：选课（课程，教师，学生）

右：有三个关系：教授（课程，教师）；上课（课程，学生）；指导（教师，学生）

Arrows in Multiway Relationships：—>means can be determined by others

Mapping Cardinality Constraints

Express the number of entities to which another entity can be associated via a relationship set.

Most useful in describing binary relationship sets.

For a binary relationship set the mapping cardinality must be one of the following types:

• One to one (<—->)
• One to many (<––>)
• Many to one (—->) (–M——1–)
• Many to many (—-) (–M—–N–)

Some elements in A and B may not be mapped to any elements in the other set

Roles in Relationships

need an entity set twice in one relationship

Entity sets of a relationship need not be distinct

Roles are indicated in E-R diagrams by labeling the lines that connect diamonds to rectangles.

Role labels are optional, and are used to clarify semantics of the relationship

Constraints约束

A constraint = an assertion about the database that must be true at all times

Part of the database schema

Very important in database design

• Give more semantics to the data
• help us better understand it
• Allow us to refer to entities (e.g, using keys)
• Enable efficient storage, data lookup, etc.

Modeling Constraints

Finding constraints is part of the modeling process.

Commonly used constraints:

*Keys: resident identification card number uniquely identifies a person.

Single-value constraints: a person can have only one father.

*Referential integrity constraints: if you work for a company, it must exist in the database.

*Domain constraints: peoples’ ages are between 0 and 150.

General constraints: all others (at most 50 students enroll in a class)

Keys in E/R Diagrams

A super key of an entity set is a set of one or more attributes whose values uniquely determine each entity.

A candidate key of an entity set is a minimal super key

Although several candidate keys may exist, one of the candidate keys is selected to be the primary key.

Every entity set must have a key

So that the entity can be identified

A key can consist of more than one attribute

There can be more than one key for an entity set

one key will be designated as primary key

ER Modeling Principle

Design Techniques

• be faithful
• KISS (keep it simple and stupid)
• Avoid redundancy.
• Limit the use of weak entity sets.
• Don’t use an entity set when an attribute will do.

Avoiding Redundancy

• Redundancy occurs when we say the same thing in two different ways.
• Redundancy wastes space and (more importantly) encourages inconsistency.
  • The two instances of the same fact may become inconsistent if we change one and forget to change the other, related version.

Entity Sets Versus Attributes

• An entity set should satisfy at least one of the following conditions:
  • It is more than the name of something; it has at least one nonkey attribute.
  • It is the “many” in a many-one or many-many relationship.

3.Logical Model - Relational Model

Logical Data Model (LDM)

Represent the abstract information structure of business domain

Unambiguous, formalized definition on the model

Implemented in DBMS, adjusted to achieve efficiency on computing system.

Three elements of logical data model:

• Data structure
• Data operation
• Data constraints

The evolution of LDM

物理模型[–>文件模型–>层次模型–>网状模型–>关系模型（most popular LDM）–>XML模型/面向对象模型–>]概念模型

Structure of Relational Model

Relational Database

Database that adopts relational model

Database Modeling & Implementation

Ideas

->Database Model (E/R, ODL)( Diagrams (E/R))

->Relational Schema(Tables: column names: attributes rows: tuples)

->Physical storage(Complex file organization and index structures.)

ER Model vs. Relational Model

Both are used to model data

ER model has many concepts

• entities, relations, attributes, etc.
• well-suited for capturing the app. requirements
• not well-suited for computer implementation
• (does not even have operations on its structures)

Relational model

• has just a single concept: relation
• world is represented with a collection of tables
• well-suited for efficient manipulations on computers

Schema vs. instance

Analogy with programming languages:

• Schema = type
• Instance = value

Important distinction:

• Database Schema = stable over long periods of time
• Database Instance = changes constantly, as data is inserted/updated/deleted

Schema图示

• Corresponds to the programming language concept of type definition
• E.g. Java
  • String movie = “Spider man”;

The Schema of a Relation:

• Relation name plus attribute names
• E.g. Product(Name, Price, Category, Manufacturer)
  • In practice we add the domain for each attribute

The Schema of a Database

• A set of relation schemas
• E.g. Product(Name, Price, Category, Manufacturer), Vendor(Name, Address, Phone), . . . . . . .

Instance实例

• Corresponds to the programming-language concept of the value of a variable
• E.g. Java
  • String movie = “Spider man”;

Relational schema = R(A1,…,Ak):

• Instance = relation with k attributes (of “type” R)
  • values of corresponding domains

Database schema = R1(…), R2(…), …, Rn(…)

• Instance = n relations, of types R 1, R 2, …, Rn

Updates

The database maintains a current database state.

Updates to the data:

​ 1) add a tuple

​ 2) delete a tuple

​ 3) modify an attribute in a tuple

Updates to the data happen very frequently.

Cartesian product笛卡尔积

• D1 = {a, b}
• D2 = {c, d}
• D3 = {e, f, g}

D1XD2XD3 = {(a, c, e), (a, c, f), (a, c, g), (a, d, e), (a, d, f), (a, d, g), (b, c, e), (b, c, f), (b, c, g), (b, d, e), (b, d, f), (b, d, g)}

由定义可以看出，笛卡尔积也是一个集合,其中：

1. 元素中的每一个di叫做一个分量(Component)，来自相应的域（di∈Di）
2. 每一个元素（d1，d2，d3，…，dn）叫做一个n元组（n-tuple），简称元组（Tuple）。但元组不是di的集合，元组的每个分量（di）是按序排列的。如：

（1，2，3）≠（2，3，1）≠（1，3，2）；

而集合中的元素是没有排序次序的，如（1，2，3）=（2，3，1）=（1，3，2）。

Mathematical Definitions of Relations

Relation is the subset of Cartesian product

Relation keeps the meaningful tuple in the Cartesian product

Relation has FINITE tuples(关系有有限元组)

Relation vs. Cartesian product

Relation as table

Rows = tuples

Columns = components

Names of columns = attributes

Relation name + set of attribute names= schema

REL (A 1,A 2,…,An)

Set theoretic

Domain — set of values: like a data type

Cartesian product: D1 X D2 X … X Dn

n-tuples (V1,V2,…,Vn)

Relation=subset of Cartesian product of one or more domains

FINITE only; empty set allowed

Tuples(元组) = members of a relation inst.

Arity （元）= number of domains

Components （分量）= values in a tuple

Domains(域) — corresp. with attributes

Cardinality（基数）= max number of tuples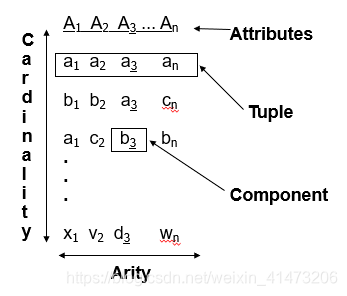#### Database

A database consists of multiple relations

Information about an enterprise is broken up into parts, with each relation storing one part of the information

account : stores information about accounts
depositor : stores information about which customer owns which account
customer : stores information about customers

Relation’s features

Tuples with same value are not allowed

Relations are Unordered

• Order of tuples is irrelevant (tuples may be stored in an arbitrary order)
• Order of Attributes is also irrelevant

Attribute values must comply with domain constraint

• 同一属性名下的各个属性值必须来自同一个域，是同一类型的数据

Each attribute must has a different name

Different attributes can use a same domain

Attribute values are required to be atomic; that is, indivisible(不可再分的)

• E.g. the value of an attribute can be an account number, but cannot be a set of account numbers
• Also the attribute can’t be a composite one

translating from ER to relational model

Basic cases

• Relationships to Relations: entity set E = relation with attributes of E
• Relationships to Relations: relationship R = relation with attributes being keys of related entity sets + attributes of R
  • watch out for attribute name conflicts

Special cases

• many-one, one-one relations: combining two relations
  • It is OK to combine the relation for an entity-set E with the relation R for a many-one relationship from E to another entity set.
    • 多对一的时候将关系合并到多的一方的E中
    • Example: Drinkers(name, addr) and Favorite(drinker, beer) combine to make Drinker1(name, addr, favoriteBeer).
    • One-One relationship: Any side is okay
• translating weak entity sets

Constraints of Relational Model

Integrity Constraints

Purpose: prevent semantic inconsistencies in data（防止数据中的语义不一致）

predicates on the database

must always be true (that is, checked whenever database gets updated)

Main types of IC’s:

Domain Integrity Constraints(1 table)

• Attach constraints to values of attributes
• Enhances types system
• Also checks the Null value
  • It is possible for tuples to have a null value, denoted by null, for some of their attributes
  • null signifies an unknown value or that a value does not exist.
• e.g., values of age must less than 120

Entity Integrity Constraints(1 table)

• Defined by Primary Key
• A primary key is a combination of columns which uniquely specify a row
• A primary key cannot allow null values. (You cannot define a primary key on columns that allow nulls.)
• Each table can have at most one primary key.
• e.g., 2 acts can’t share the same act_no

Referential Integrity constraints ( 2 tables)

• e.g., b_names associated w/ loans must be names of real branches

Unique Key Constraints

A unique key can uniquely identify each row in a table. That is, no two distinct rows in a table can have the same value (or combination of values) in those columns constrained by unique key.

A unique key can allow null values. (You can define a unique key on columns that allow nulls.)

Each table can have multiple unique keys

Referential Integrity Constraints

Referential integrity is a property of data which, when satisfied, requires every value of one attribute (column) of a relation (table) to exist as a value of another attribute in a different (or the same) relation (table).

For referential integrity to hold in a relational database, any field in a table that is declared a foreign key can contain only values from a parent table’s primary key or a candidate key

Unary relation referencing

Relational-Algebra-Operations

Querying the Database

Goal: specify what we want from our database

Could write in C++/Java, but bad idea

Instead use high-level query languages:

Theoretical: Relational Algebra, Datalog

Practical: SQL

Relational algebra: a basic set of operations on relations that provide the basic principles.

Motivation: The Stack

To use the “stack” data structure in my program, I need to know

• what a stack looks like
• what (useful) operations I can perform on a stack
  • PUSH and POP

Next, I look for an implementation of stack

• browse the Web
• find many of them
• choose one, say LEDA(an open source algorithm library)

LEDA already implement PUSH and POP

It also gives me a simple language L, in which to define a stack and call PUSH and POP

• S = init_stack(int);
• S.push(3); S.push(5);
• int x = S.pop();

Can also define an expression of operations on stacks

• T = init_stack(int);
• T.push(S.pop());

To summarize, I know

• definition of stack
• its operations (PUSH, POP): that is, a stack algebra
• an implementation called LEDA, which tells me how to call PUSH and POP in a language L
• I can use these implementations to manipulate stacks
• LEDA hides the implementation details
• LEDA optimizes implementation of PUSH and POP

Algebra

Mathematical system consisting of:

• Operands （运算对象）— variables or values from which new values can be constructed.
• Operators （运算符）— symbols denoting procedures that construct new values from given values.

Relational Algebra

An algebra whose operands are relations or variables that represent relations.

Operators are designed to do the most common things that we need to do with relations in a database.

• The result is an algebra that can be used as a query language for relations.

Operators: relations as input, new relation as output

Five basic RA operations:

• Basic Set Operations
  • union, difference (no intersection, no complement)
• Selection
• Projection
• Cartesian Product

Derived operations:

• Intersection, complement
• Joins (natural, equi-join, theta join, semi-join)

Five Basic RA Operations

Set Operations

Binary operations

• Union
• difference

Unary operations

• Selection
• Projection

Cartesian Product

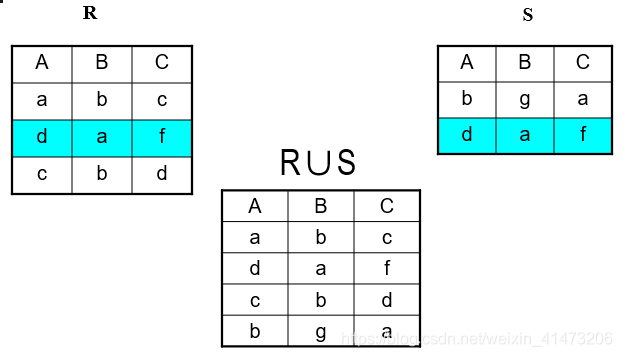
Set Operations: Union

Union: all tuples in R1 or R2

No duplicate tuples

Notation: R1 U R2

R1, R2 must have the same schema

R1 U R2 has the same schema as R1, R2

Example:
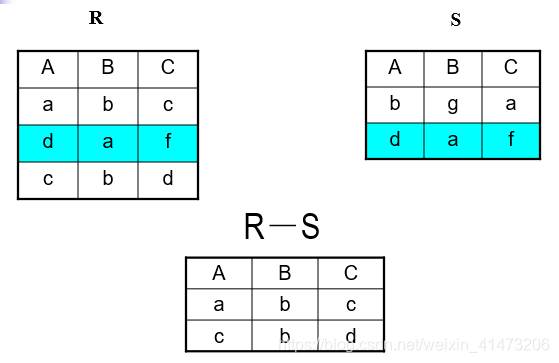
##### Set Operations: Difference

Difference: all tuples in R1 and not in R2

Notation: R1 – R2

R1, R2 must have the same schema

R1 - R2 has the same schema as R1, R2

Example：

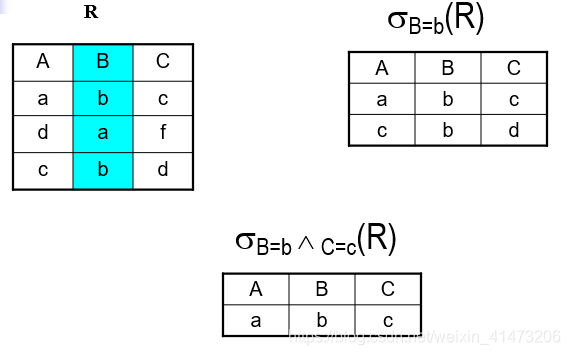
Selection选择运算

Returns all tuples which satisfy a condition

Notation: σc(R)\sigma_{c}(R)σc​(R)

c is a condition: =, <, >, and, or, not

Output schema: same as input schema

##### Projection投影运算

Unary operation: returns certain columns

Notation: ΠA1,…,An(R)\Pi_{A1,…,An} (R)ΠA1,…,An​(R)

Input schema R(B1,…,Bm)

Condition: {A1, …, An}包含于{B1, …, Bm}

Output schema S(A1,…,An)

no duplicate elimination

Cartesian Product

Each tuple in R1 with each tuple in R2

Notation: R1 x R2

Input schemas R1(A1,…,An), R2(B1,…,Bm)

Output schema is S(A1, …, An, B1, …, Bm*)*

Notation: R1 x R2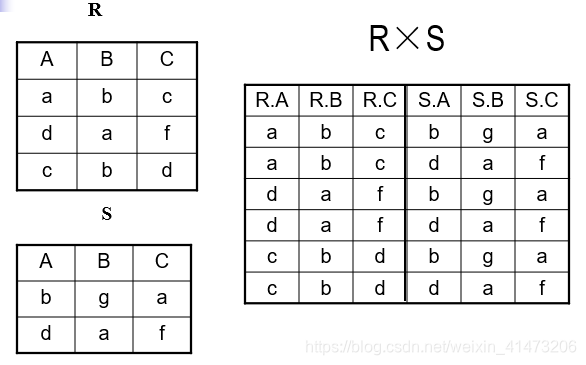

Derived RA Operations

1) Intersection
2) Most importantly: Join
3) Division

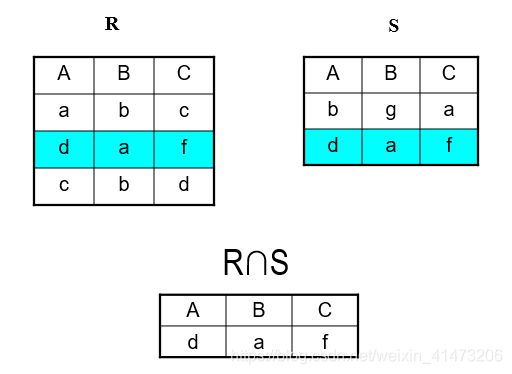
Set Operations: Intersection

Difference: all tuples both in R1 and in R2

Notation: R1∩R2

R1, R2 must have the same schema

R1∩R2 has the same schema as R1, R2

Intersection is derived: R1∩R2 = R1 – (R1 – R2)

Joins连接

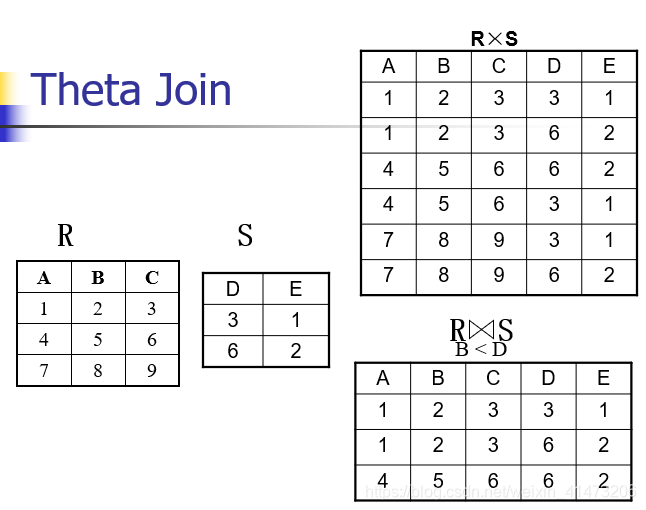
Theta join

A join that involves a predicate

Notation: R1|X|cR2 where c is a condition

Input schemas: R1(A1,…,An), R2(B1,…,Bm)

Output schema: S(A1,…,An,B1,…,Bm)

Derived operator:R1∣X∣cR2=σc(R1xR2)R1|X|_cR2 = \sigma_c(R1 x R2)R1∣X∣c​R2=σc​(R1xR2)

Natural join

A frequent type of join connects two relations by:

Equating attributes of the same name, and

Projecting out one copy of each pair of equated attributes.

Called natural join.

Denoted R3 := R1 JOIN R2.

Notation: R1|X|R2

Input Schema: R1(A1, …, An), R2(B1, …, Bm)

Output Schema: S(C1,…,Cp)

Where {C1, …, Cp} = {A1, …, An} U {B1, …, Bm}

Meaning: combine all pairs of tuples in R1 and R2 that agree on the attributes:

{A1,…,An}|X|{B1,…, Bm} (called the join attributes)

Equivalent to a cross product followed by selection

Equi-join

Most frequently used in practice: R1|X|A=B_{A=B}A=B​R2

Natural join is a particular case of equi-join

A lot of research on how to do it efficiently

Outer join

An extension of the join operation that avoids loss of information.

Computes the join and then adds tuples form one relation that does not match tuples in the other relation to the result of the join.

Uses null values to signify the unmatched values

Subtypes: left outer joins, right outer joins, and full outer joins

• 左外连接 = 自然连接 + 左侧表中失配的元组。
• 右外连接 = 自然连接 + 右侧表中失配的元组。
• 全外连接 = 自然连接 + 两侧表中失配的元组。

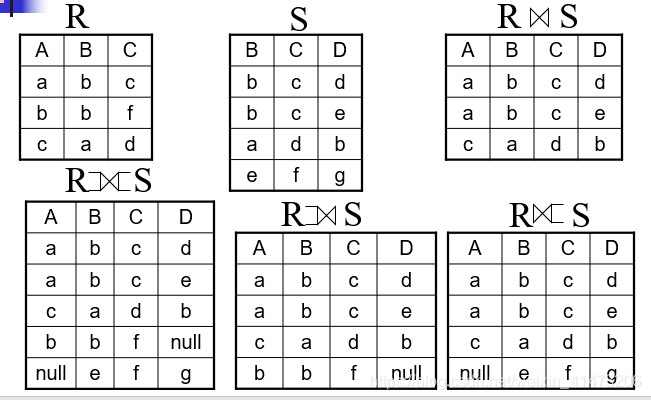
etc.

Division(除运算)

R（X，Y）是被除关系

S（Y）是除关系

商关系由R中某些X属性值构成，其中的任一X值所对应的一组Y值都包含除关系S。

除运算常用于包含语义“至少…”的语义的查询或运算

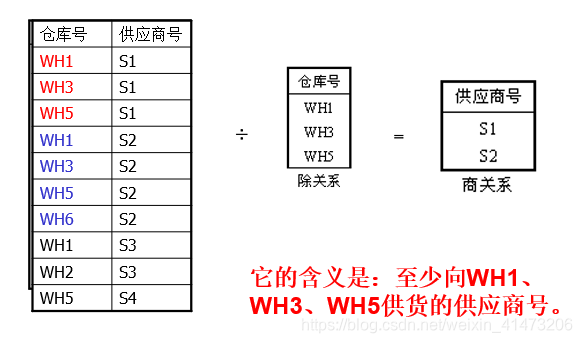
Complex Query

1. σ\sigmaσ选择运算->|X|自然连接运算->Π\PiΠ投影运算

Exercise