跳跃表 skip list
关键词: 跳跃表/skip list/skiplist
1. 跳跃表
skip List是一种随机化的数据结构,基于并联的链表,实现简单,插入、删除、查找的复杂度均为O(logN)(大多数情况下),因为其性能匹敌红黑树且实现较为简单,因此在很多著名项目都用跳表来代替红黑树,例如LevelDB、Redis的底层存储结构就是用的SkipList。
目前常用的key-value数据结构有三种:Hash表、红黑树、SkipList,它们各自有着不同的优缺点:
- Hash表:插入、查找最快,为O(1);如使用链表实现则可实现无锁;数据有序化需要显式的排序操作。
- 红黑树:插入、查找为O(logn),但常数项较小;无锁实现的复杂性很高,一般需要加锁;数据天然有序。
- SkipList:插入、查找为O(logn),但常数项比红黑树要大;底层结构为链表,可无锁实现;数据天然有序。
2. 基本数据结构及其实现
一个跳表,应该具有以下特征:
- 跳表由多层(level)组成;
通常是10-20层,leveldb中默认为12层。 - 跳表的第0层包含所有的元素;
且节点值是有序的。 - 每一层都是有序的链表;
层数越高应越稀疏,这样在高层次中能'跳过’许多的不符合条件的数据。 - 如果元素x出现在第i层,则所有比i小的层都包含x;
- 每个节点包含key及其对应的value和一个指向该节点第n层的下个节点的指针数组
x->next[level]表示第level层的x的下一个节点
从上面的结构也可以看出,跳跃表的核心思想就是,每一个节点既包含指向下一个节点的指针,也可能包含很多个指向后续节点的指针,这样在查找、插入、删除某个节点的过程中,可以避免一些不必要的节点,从而提高效率。
示意图:

2.1. 查找 search
查询的第一个比vx大的节点的前一个值,看是否相等。相等则存在,否则查找下一层,直到层数为0。
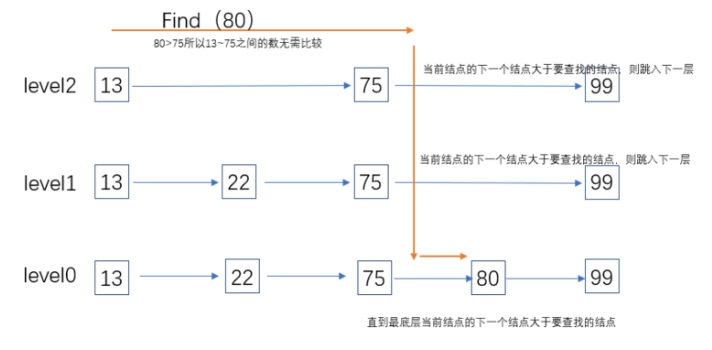
从最高层(此处为2)开始:
- level2找到结点Node75小于80,且level2.Node75->next 大于80,则进入level1查找(此处已经跳过了13~75中间的结点(22),
- level1.Node75 < 80 < level1.Node75->next,进入level0
- level0.Node75->next 等于80,找到结点
2.2. 插入
假设插入一新键值key,值为84,level为当前层
1、从最高层开始找到每一层比84大的节点的前一个值,存入prev[level]。
2.3. 删除
删除操作类似于插入操作,包含如下3步:1、查找到需要删除的结点 2、删除结点 3、调整指针
3. 跳跃表性能分析
在使用抛硬币法决定层数的前提下跳跃表可以视为实现二分查找的有序链表。
接下来的讨论也是基于这一前提条件。
3.1. 时间复杂度
查找元素的过程是从最高级索引开始,一层一层遍历最后下沉到原始链表。 所以,时间复杂度 = 索引的高度 * 每层索引遍历元素的个数。
先求跳表的索引高度。
假设每两个下层结点会抽出一个作为上层索引的结点,原始的链表有n个元素,则一级索引有n/2 个元素、二级索引有 n/4 个元素、k级索引就有 n/2k个元素。
最高级索引一般有2个元素,即:最高级索引 h 满足 2 = n/2h,即 h = log2n - 1,最高级索引 h 为索引层的高度加上原始数据一层,跳表的总高度 h = log2n。
因为结点划分近似于二分法,所以当每级索引都是两个结点抽出一个结点作为上一级索引的结点时,每一层最多遍历3个结点。
跳表的索引高度 h = log2n,且每层索引最多遍历 3 个元素。所以跳表中查找一个元素的时间复杂度为 O(3*logn),省略常数即:O(logn)。
3.2. 空间复杂度
假如原始链表包含 n 个元素,则一级索引元素个数为 n/2、二级索引元素个数为 n/4、三级索引元素个数为 n/8 以此类推。
所以,索引节点的总和是:n/2 n/4 n/8 … 8 4 2 = n-2,空间复杂度是 O(n)。
另外,索引结点往往只需要存储key和几个指针,并不需要存储完整的对象,所以当对象比索引结点大很多时,索引占用的额外空间就可以忽略了。
4. 总结
- 跳表是可以实现类二分查找的有序链表;
- 每个元素插入时随机生成它的level;
- 最底层包含所有的元素;
- 如果一个元素出现在level(x),那么它肯定出现在x以下的level中;
- 每个索引节点包含两个指针,一个向下,一个向右;
- 跳表查询、插入、删除的时间复杂度为O(log n),与平衡二叉树接近;
有一个比较大的疑问?
抛硬币法究竟能不能实现上文所讨论的类二分式索引;
本质上它是随机的,但在大规模数据下是不是类二分式索引仍需要数学验证。。。
虽然这一因素并不影响上文所给出的复杂度的量级,但具体性能并不能完全确定。
5. 跳跃表代码实现 python
#!/usr/bin/env python
#coding:utf-8
"""
----------------------------------------
description:
author: sss
date:
----------------------------------------
change:
----------------------------------------
"""
__author__ = 'sss'
import random
# 全局设置
# skiplist max level
MAX_LEVEL = 10
# 全局方法
def pr_type(i, info=''):
print(info, i, type(i))
# 跳跃表结点
class SkipListNode(object):
def __init__(self, level=0, val=None):
"""
跳跃表结点初始化
:param level: 结点层数
:param val: 存储值
"""
self.val = val
self.next = [None]*level
def __repr__(self):
return str(self.val)
# 跳跃表
class SkipList(object):
"""
update_list:主要方法。作用是从跳跃表的最顶层开始依次向下查找,
找到该层级中val的前一元素并保存,重复直至底层。
返回列表update,update[0]表示0层val前一元素,以此类推。
该方法可以使得插入删除操作变得更加简单。
random_level:跳跃表插入新结点,需要生成该结点的层数。
该方法的思路是用抛硬币法随机生成层数,
如果正面(random.randint(0, 1) == 1)则层数加一,直到抛出反面为止。
MAX_DEPTH限定最大层数。
"""
def __init__(self):
"""
skiplist initalization
"""
self.head = SkipListNode()
self.size = 0
@staticmethod
def random_level():
"""
返回随机层数,如果大于最大层数则返回最大层数
:return: int; random level
"""
k = 1
while random.randint(0, 1):
k += 1
if k == MAX_LEVEL:
break
return k
def update_list(self, val):
update = [None] * len(self.head.next)
x = self.head
for i in reversed(range(len(self.head.next))):
while x.next[i] is not None and \
x.next[i].val < val:
x = x.next[i]
update[i] = x
return update
def search(self, val, update=None):
if update is None:
update = self.update_list(val)
if len(update) > 0:
candidate = update[0].next[0]
if candidate is not None and candidate.val == val:
return candidate
return None
def insert(self, val):
node = SkipListNode(self.random_level(), val)
while len(self.head.next) < len(node.next):
self.head.next.append(None)
update = self.update_list(val)
if self.search(val, update) is None:
for i in range(len(node.next)):
node.next[i] = update[i].next[i]
update[i].next[i] = node
def remove(self, val):
update = self.update_list(val)
x = self.search(val, update)
if x is not None:
for i in range(len(x.next)):
update[i].next[i] = x.next[i]
if self.head.next[i] is None:
self.head.next = self.head.next[:i]
return
def traversal(self):
for i in reversed(range(len(self.head.next))):
x = self.head
line = []
while x.next[i] is not None:
line.append(str(x.next[i].val))
x = x.next[i]
print('line{}:'.format(i+1) + '->'.join(line))
def _test():
pass
if __name__ == '__main__':
_test()
pass
# pr_type('s')



 浙公网安备 33010602011771号
浙公网安备 33010602011771号