两个有序数组求中位数算法

最近研究一个算法表示很有收获，加深了对二分法的运用，记录如下：

原题

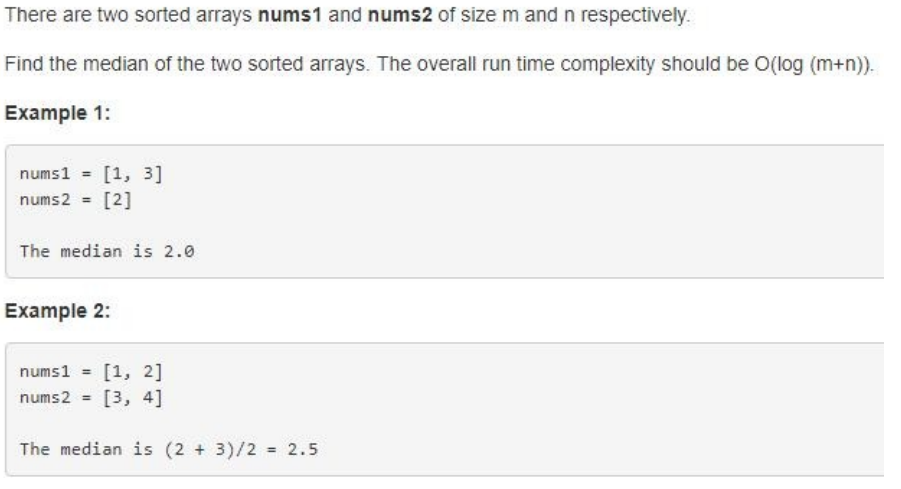
解法一

点击查看代码

//丑陋的实现，但时间复杂度 O((m+n)/2)；空间复杂度O(1)
    private static double getAns1(int[] nums1, int[] nums2) {
        int length = nums1.length + nums2.length;
        int medianIndex = length / 2;
        int curr = 0;
        int i = 0;
        int flag = 0;//标识遍历完短的数组后剩下的需要处理数组，1表示第一个数组需要继续处理，2表示第二个数组需要继续处理
        int nextCmp = 0;
        int nextCmp2 = 0;
        //取两个数组的数进行比较，直到（找到中位数 或 未找到但一个数组遍历完）退出
        for (int j = 0, k = 0; i < length; i++) {
            if (nums1[j] < nums2[k]) {
                curr = nums1[j];
                nextCmp = nums2[k];
                if (j + 1 < nums1.length) {
                    nextCmp2 = nums1[++j];
                } else {
                    if(++k==nums2.length) {//防止越界
                        nextCmp2 = nums2[--k];
                    } else {
                        nextCmp2 = nums2[k];
                    }
                    flag = 2;
                }
            } else {
                curr = nums2[k];
                nextCmp = nums1[j];
                if (k + 1 < nums2.length) {
                    nextCmp2 = nums2[++k];
                } else {
                    if(++j==nums1.length) {//防止越界
                        nextCmp2 = nums1[--j];
                    } else {
                        nextCmp2 = nums1[j];
                    }
                    flag = 1;
                }
            }
            System.out.println("curr1:" + curr);
            if (i + 1 == medianIndex) {
                int next = Math.min(nextCmp, nextCmp2);
                return length % 2 == 0 ? (curr + next) / 2.0 : next;
            }
            if (flag > 0) {
                break;
            }
        }

        //根据flag的值在剩余未处理完的数组中找到中位数
        if (flag == 1) {
            for (int i2 = i + 1; i2 < length; i2++) {
                curr = nums1[i2 - nums2.length];
                System.out.println("curr2:" + curr);
                if (i2 + 1 == medianIndex) {
                    int next = nums1[i2 - nums2.length + 1];
                    return length % 2 == 0 ? (curr + next) / 2.0 : next;
                }
            }
        }
        if (flag == 2) {
            for (int i2 = i + 1; i2 < length; i2++) {
                curr = nums2[i2 - nums1.length];
                System.out.println("curr2:" + curr);
                if (i2 + 1 == medianIndex) {
                    int next = nums2[i2 - nums1.length + 1];
                    return length % 2 == 0 ? (curr + next) / 2.0 : next;
                }
            }
        }
        return 0.0;
    }

解法二

点击查看代码

/**
     * 优雅多了，主要在于判断条件 (aStart < len1 && (bStart >= len2 || nums1[aStart] < nums2[bStart])) 的理解
     * 此法也适用于有序数组合并
     * 时间复杂度O((m+n)/2)),空间复杂度O(1)
     */
    private static double getAns2(int[] nums1, int[] nums2) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int len = len1 + len2;
        int pre = 0, curr = 0;
        //遍历 n/2 +1次
        for (int i = 0, aStart = 0, bStart = 0; i <= len / 2; i++) {
            pre = curr;
            if (aStart < len1 && (bStart >= len2 || nums1[aStart] < nums2[bStart])) {
                curr = nums1[aStart++];
            } else {
                curr = nums2[bStart++];
            }
        }
        return (len & 1) == 0 ? (pre + curr) / 2.0 : curr;
    }

解法三

点击查看代码

    /**
     * 此法保证切割的是短的数组，每次切割排除一半，所以时间复杂度 O(log(min(m+n))), 空间复杂度O(1)
     * 利用二分法切割两个数组，保证：
     * 条件1：【数组1.左+数组2.左】的数目 等于或多1于 【数组1.右+数组2.右】的数目
     * 条件2：【数组1.左.max】 <= 【数组2.右.min】 且 【数组2.左.max】 <= 【数组1.右.min】
     * 条件3: i==0 或 i==m 或 j==0 或 j==n
     * 最终条件：(条件1 && 条件2) || 条件3
     * 则此时：
     * 偶数长度中位数：【数组1.左+数组2.左】.max + 【数组1.右+数组2.右】.min) / 2
     * 奇数长度中位数：【数组1.左+数组2.左】.max
     */
    private static double getAns3(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;
        //保证m<=n
        if (m > n) {
            return getAns3(nums2, nums1);
        }
        int start = 0, end = m;
        //i表示数组1的切割位置，j表示数组2的切割位
        int i = (start + end + 1) >> 1;//这里保证了i!=0
        int j = (m + n + 1) / 2 - i;
        while (true) {
            if (j != n && nums1[i - 1] > nums2[j]) {
                end = i;
                //此处条件1达成
                // 由 i + j == m-i + n-j 和 i + j == m-i + n-j + 1 推导
                i = (start + end) >> 1;//往左切保证可以切到最左边也就是i==0
                j = (m + n + 1) / 2 - i;
            } else if (i != m && nums2[j - 1] > nums1[i]) {
                start = i;
                //此处条件1达成
                // 由 i + j == m-i + n-j 和 i + j == m-i + n-j + 1 推导
                i = (start + end + 1) >> 1;//往右切保证可以切到最右边也就是i==m
                j = (m + n + 1) / 2 - i;
            } else {
                //此处条件1和条件2达成
                break;
            }
            //此处条件3达成
            if (i == 0 || j == 0 || i == m || j == n) {
                break;
            }
        }
        int maxLeft;
        int minRight;
        if (i == 0) {
            maxLeft = nums2[j - 1];
        } else if (j == 0) {
            maxLeft = nums1[i - 1];
        } else {
            maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
        }
        if (i == m) {
            minRight = nums2[j];
        } else if (j == n) {
            minRight = nums1[i];
        } else {
            minRight = Math.min(nums1[i], nums2[j]);
        }

        return ((m + n) & 1) == 0 ? (maxLeft + minRight) / 2.0 : maxLeft;
    }
}