一.平衡二叉树 VS 搜扫二叉树
1. 平衡二叉树:解决在树的结构搜扫的时候,防止搜扫数据呈现出斜二叉树的数据结构,因此在节点插入和删除的时候,自动的调节树的数据结构,让树搜索速度达到log(N)的时间复杂度。
下面二叉搜索树的构造和其各种运用Delete,Insert
对于二叉搜索树删除:1.度为2节点删除,要么从左子树选择最大节点代替此删除节点,或者从右子树中选择最小的节点代替此节点。2.度不大于1的节点:将左节点或者右节点覆盖此为位置T=T->Left。
#include<iostream> using namespace std; #define ElementType int //对二叉搜扫树各种功能模拟 typedef struct TreeNode{ ElementType Data; struct TreeNode *LeftNode; struct TreeNode *RightNode; }*BinTree,BinTreeNode; BinTree CreateBinSearch() { BinTree root=new BinTreeNode,ptr,Rear; root->LeftNode=NULL;root->RightNode=NULL;root->Data=NULL; int num=100; cout<<"输出-1值表示停止"<<endl; while(true) { cin>>num; ptr=root; if(num==-1) break; if(ptr->Data==NULL) { ptr->Data=num;//空树 } else { Rear=new BinTreeNode; Rear->Data=num;Rear->LeftNode=NULL;Rear->RightNode=NULL; while(ptr) { if(num<ptr->Data) { if(ptr->LeftNode==NULL) { ptr->LeftNode=Rear; break;} else ptr=ptr->RightNode; } else{ if (ptr->RightNode==NULL) { {ptr->RightNode=Rear;break;} }else { ptr=ptr->RightNode; } } } } } return root; } BinTree Insert(BinTree Rear,int X) { //采用递归的形式对新输入的值进行插入,不断对值递归调用直到最后进行 if(!Rear) { //最后递归找到插入位置最后对位置进行插入 cout<<"这个是一颗空树"<<endl; Rear->Data=X;Rear->LeftNode=NULL;Rear->RightNode=NULL; } //使用尾部递归方式 else{ if(Rear->Data>X) Insert(Rear->LeftNode,X); else Insert(Rear->RightNode,X); } return Rear; } BinTree FindMin(BinTree Rear) { /*while(Rear->LeftNode) Rear=Rear->LeftNode; return Rear;*/ //采用递归的话 if(!Rear) return NULL; else if(!Rear->LeftNode) return Rear; else FindMin(Rear->LeftNode); } BinTree Delete(BinTree Rear,int delete_value) { //对于删除节点分为两种情况,节点度=2,只能从此节点的左子树中找一个最大值代替此删除点 //度=1,删除此点,将其单个子节点填补其位置就行 if(!Rear) cout<<"删除的点没有找到"<<endl ; //开始寻找要删除点->Data=delete_value; if(delete_value>Rear->Data) Delete(Rear->RightNode,delete_value); else if(Rear->Data<delete_value) Delete(Rear->LeftNode,delete_value); else { //刚好找到其位置 BinTree tmp; if(Rear->LeftNode && Rear->RightNode) { tmp=FindMin(Rear->RightNode); Rear->Data=tmp->Data; //在从右子树中删除最小的节点,是一个叶子节点 Delete(Rear->RightNode,tmp->Data); } else{ //最多只有一个节点 if(Rear->LeftNode) Rear=Rear->LeftNode; else Rear=Rear->RightNode; } } } int main() { BinTree rootNode; rootNode=CreateBinSearch(); cout<<"********向二叉搜扫树中插入值************"<<endl; int Insert_numbel; cin>>Insert_numbel; rootNode=Insert(rootNode,Insert_numbel); cout<<"********向二叉搜扫树中删除值************"<<endl; int Y; cin>>Y; Delete(rootNode,Y); return 0; }
2. 在调节树的数据结构的,通过平衡因子BF调节其结构;BF=h(x-Right)-h(x-left)---节点X的右子树高度减去左子树高度
3.根据插入和删除的节点不同,将造成不平衡节点分为4种方式,LL,RR,LR,RL 四种格式
规则:调整之后必须要保持其是二叉搜索树的特性。
LL: 由于B节点左子树插入节点导致A点失去平衡:以B节点为轴心,A节点顺时针循转到B的右子树中,B原来的右子树变为A的左子树
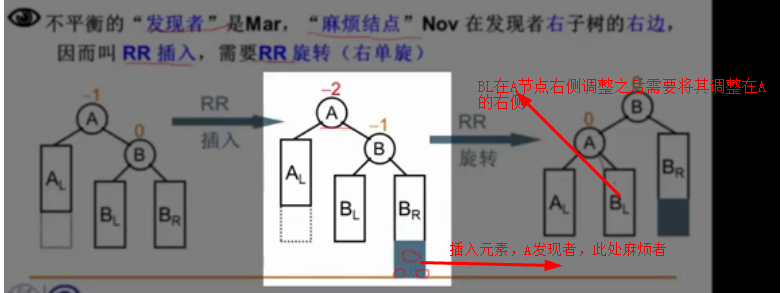
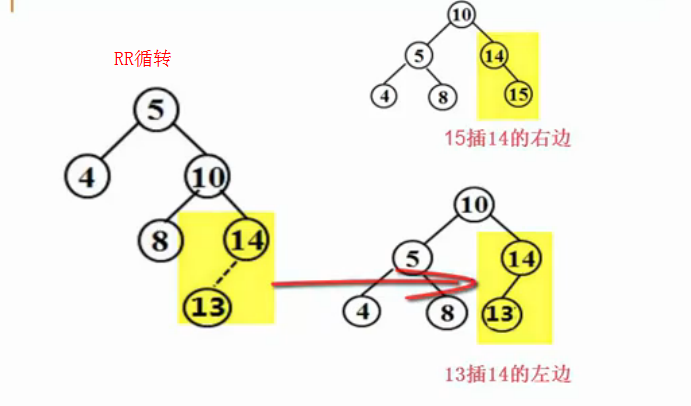
LR:B节点右子插入新的节点导致A节点失去平衡,插入在被破坏者May的左子树的右子树上,因此做LR循转
Mar调整到根节点上,A-B-C:调整为C-B-A。C是B的右子树节点。

判断其是单旋 Vs双旋 插入B节点的后面
比较 破坏者C,被破坏者A,A>B>C(A<B<C):A的左子树左子树上LL(右子树右子树RR);
如果C节点在中间A>C>B(A<C<B): 做双旋转,A的左子树右子树上LR旋转(A 的右子树左子树上RL旋转)。
#include<iostream> #include<queue> using namespace std; #define ElementType int typedef struct AVLTree{ ElementType Data; int Height;//计算单个节点上的树的高度 AVLTree *LeftNode; AVLTree *RightNode; //构造函数初始化 AVLTree():Data( NULL),Height(NULL),LeftNode(NULL),RightNode(NULL){} }*AvlTree,AvlTreeNode; int max(int a,int b) { return a>b?a:b; } int GetHeight(AvlTree T) { if (!T) return -1; else return T->Height; if (!T) return 0; else return max(GetHeight(T->LeftNode),GetHeight(T->RightNode))+1; } AvlTree SigngleRoatedWithLeft(AvlTree T) { //左单旋 AvlTree T1; T1=T->LeftNode; T->LeftNode=T1->RightNode; T1->RightNode=T; //更新新的矩阵值,高的指树的高度 T->Height=max(GetHeight(T->LeftNode),GetHeight(T->RightNode))+1; T1->Height=max(GetHeight(T1->LeftNode),T->Height)+1; return T1; } AvlTree SigngleRoatedWithRight(AvlTree T) {//右单旋 AvlTree T1; T1=T->RightNode; T->RightNode=T1->LeftNode; T1->LeftNode=T; //更新新的矩阵值,高的指树的高度 T->Height=max(GetHeight(T->LeftNode),GetHeight(T->RightNode))+1; T1->Height=max(GetHeight(T1->LeftNode),T->Height)+1; return T1; } AvlTree DoubleRoatedLeftandRight(AvlTree A) { //双旋,左右双旋,先做右旋修改A->left //A 节点右一个左节点B,B有一个右节点C A->LeftNode=SigngleRoatedWithRight(A->LeftNode); //对A做左旋 return SigngleRoatedWithLeft(A); } AvlTree DoubleRoatedRightandLeft(AvlTree A) { //双旋,左右双旋,先做右旋修改A->left //A 节点右一个左节点B,B有一个右节点C //对A-.right做左旋 A->RightNode=SigngleRoatedWithLeft(A->RightNode); //对A做左旋 return SigngleRoatedWithRight(A); } AvlTree Insert(ElementType X,AvlTree T) { if(!T)//判断其是否是空树 {//t通过递归建立树 T=new AvlTreeNode; T->Data=X; T->Height=0; } else if(X<T->Data) { /*插入到左子树中*/ T->LeftNode=Insert(X,T->LeftNode); if(GetHeight(T->LeftNode)-GetHeight(T->RightNode)==2) { if(X<T->LeftNode->Data) { T=SigngleRoatedWithLeft(T);//左单旋 } else{ T=DoubleRoatedLeftandRight(T);//左右单旋 } } } else if(X>T->Data) { T->RightNode=Insert(X,T->RightNode); if(GetHeight(T->LeftNode)-GetHeight(T->RightNode)==-2) { if(X>T->RightNode->Data) { T=SigngleRoatedWithRight(T);//左单旋 } else { //右左双旋 T=DoubleRoatedRightandLeft(T); } } } T->Height=max(GetHeight(T->LeftNode),GetHeight(T->RightNode))+1; return T; } void Pre_order(AvlTree T) { if(T) { cout<<T->Data<<" "; Pre_order(T->LeftNode); Pre_order(T->RightNode); } else { cout<<"#"<<" "; } } void Level_order(AvlTree T) {//使用队列对层次遍历 queue<AvlTree>Q; Q.push(T); while(T && !Q.empty()) { T=Q.front(); cout<<T->Data<<" "; if(T->LeftNode) Q.push(T->LeftNode); if(T->RightNode) Q.push(T->RightNode); Q.pop(); } } int main() { AvlTree Avl=new AvlTreeNode; //通过插入建立AVL平衡树,通过斜插; for(int i=1;i<=7;i++) { Avl=Insert(i,Avl); } //前序遍历输出 Pre_order(Avl); cout<<endl; cout<<"层次遍历"<<endl; Level_order(Avl); return 0; }

二叉平衡树采用java中泛型数据,其中加入对数据的remove处理
package Tree; import java.util.LinkedList; //12.1采用数据进行测试 public class AVLTree <AnyType> { private static class AvlNode<AnyType> { AnyType element; AvlNode<AnyType> left; AvlNode<AnyType>right; int height;//AvlTree Hegiht public AvlNode(AnyType E) { this.element=E; this.left=null; this.right=null; this.height=-1; } public AvlNode(AnyType thiselement,AvlNode<AnyType>lt,AvlNode<AnyType>rt,int h) { this.element=thiselement; this.left=lt; this.right=rt; this.height=h; } } public static AvlNode Avltree; //通过插入AVlTree private AvlNode<AnyType> insert(AnyType x,AvlNode<AnyType>t) { if(t==null) return new AvlNode(x); int compareResult=((Comparable<AnyType>) x).compareTo(t.element); if(compareResult>0) t.right=insert(x,t.right); else if(compareResult<=0) t.left=insert(x,t.left); //最后对插入树进行调整,通过遍历其中每个树的高度 return balance(t); } private int height(AvlNode<AnyType>p) { return p==null?-1:p.height; } private AvlNode<AnyType>roatedWithLeftChild(AvlNode <AnyType>k2) { //k2 平衡性被破坏的点 AvlNode<AnyType> k1=k2.left; k2.left=k1.right; k1.right=k2; //更新所在的的高度,k1上升,k2下降 k2.height=Math.max(height(k2.left),height(k2.right))+1; k1.height=Math.max(height(k1.left),k2.height)+1; return k1; } private AvlNode<AnyType>roatedWithRightChild(AvlNode <AnyType>k2) { //k2 平衡性被破坏的点 AvlNode<AnyType> k1=k2.right; k2.right=k1.left; k1.left=k2; //更新所在的的高度,k1上升,k2下降 k2.height=Math.max(height(k2.left),height(k2.right))+1; k1.height=Math.max(height(k1.right),k2.height)+1; return k1; } private AvlNode<AnyType>doubleWithLeftChild(AvlNode<AnyType>k3) { k3.left=roatedWithRightChild(k3.left); return roatedWithLeftChild(k3); } private AvlNode<AnyType>doubleWithRightChild(AvlNode<AnyType>k3) { k3.right=roatedWithLeftChild(k3.right); return roatedWithRightChild(k3); } private AvlNode<AnyType > balance (AvlNode<AnyType> t) { if(t==null) return t; if(height(t.left)-height(t.right)>1) { if(height(t.left.left)>=height(t.left.right)) //这里等于号,说明t的左树左子孙 =左子树的右子孙;这样树调整只需要进行单步的旋转就可以解决问题 t=roatedWithLeftChild(t); else t=doubleWithLeftChild(t); } else { if(height(t.right)-height(t.left)>1) if(height(t.right.right)>=height(t.right.left)) t=roatedWithRightChild(t); else t=doubleWithRightChild(t); } t.height=Math.max(height(t.left),height(t.right))+1; return t; } //数据点删除 private AvlNode<AnyType> findMin(AvlNode<AnyType>t) { if(t==null) return null; if(t.left==null) return t; return findMin(t.left); } private AvlNode <AnyType> remove (AnyType x,AvlNode <AnyType>t) { boolean flag=false; if(t==null) return null; @SuppressWarnings("unchecked") int compareResult=((Comparable<AnyType>) x).compareTo(t.element); AvlNode <AnyType> tmp=null; if(compareResult<0) { remove(x,t.left); } else if(compareResult>0) { remove(x,t.right);} else {//刚好找到其位置 flag=true; if(t.left!=null && t.right!=null) { tmp=findMin(t.right); t.element=tmp.element; t.right=remove(tmp.element,t.right); } else { //度是1 if(t.left!=null) t=t.left; else t=t.right; } } System.out.println("Flag: "+flag); return balance(t); } public static void PreOrder(AvlNode P) { if(P!=null) { System.out.print("["+P.element+"]"); PreOrder(P.left); PreOrder(P.right); } } public static void leveOrder (AvlNode P) { //使用层次遍历,使用队列 LinkedList <AvlNode>queue=new LinkedList<AvlNode>(); queue.add(P); while((P!=null) &&(!queue.isEmpty())) { P=queue.element(); System.out.print("["+P.element+"]"); if(P.left!=null) queue.add(P.left); if(P.right!=null) queue.add(P.right); queue.remove(); } } public static void main(String [] args) { System.out.println("通过insert方法建立AVLTree"); int [] Data={ 1,2,3,4,5,6,7,8}; AVLTree Tree=new AVLTree(); for(int i=0;i<Data.length;i++) { Tree.Avltree=Tree.insert(Data[i],Tree.Avltree); } System.out.println("Tree.Avltree Preorder *******:"); PreOrder(Tree.Avltree); System.out.println("Tree.Avltree Leveorder *******:"); leveOrder(Tree.Avltree); System.out.println("Tree.Avltree remove *******:"); Tree.remove(6, Tree.Avltree); leveOrder(Tree.Avltree); } }
结果:
通过insert方法建立AVLTree
Tree.Avltree Preorder *******:
[4][2][1][3][6][5][7][8]
Tree.Avltree Leveorder *******:
[4][2][6][1][3][5][7][8]
Tree.Avltree remove *******:
Flag: true
Flag: true
Flag: false
[4][2][7][1][3][5][8]



