线段树与树状数组

$$\texttt{线段树}$$

线段树是一种支持修改、用于维护区间信息的数据结构，可以在 $O(\log n)$ 的复杂度下求出一个大小为 $n$ 的数组的区间信息（如区间和、区间最大值等），也可以在同样时间复杂度下实现单点修改和区间修改等操作。

静态区间和可以使用前缀和优化，但如果有修改操作呢？当你更新一个点 $i$ 时，前缀和数组中 $i,i+1,i+2\cdots n$ 都要更新，时间复杂度来到了 $O(n)$，无法接受，这时候我们就需要使用线段树。

基本结构

假设现在有一个大小为 $5$ 的数组 $a = \{10,11,12,13,14 \}$，用线段树维护区间和如下：

\[\texttt{(上图来源 OI-wiki)} \]

\[\texttt{建树(自制)} \]

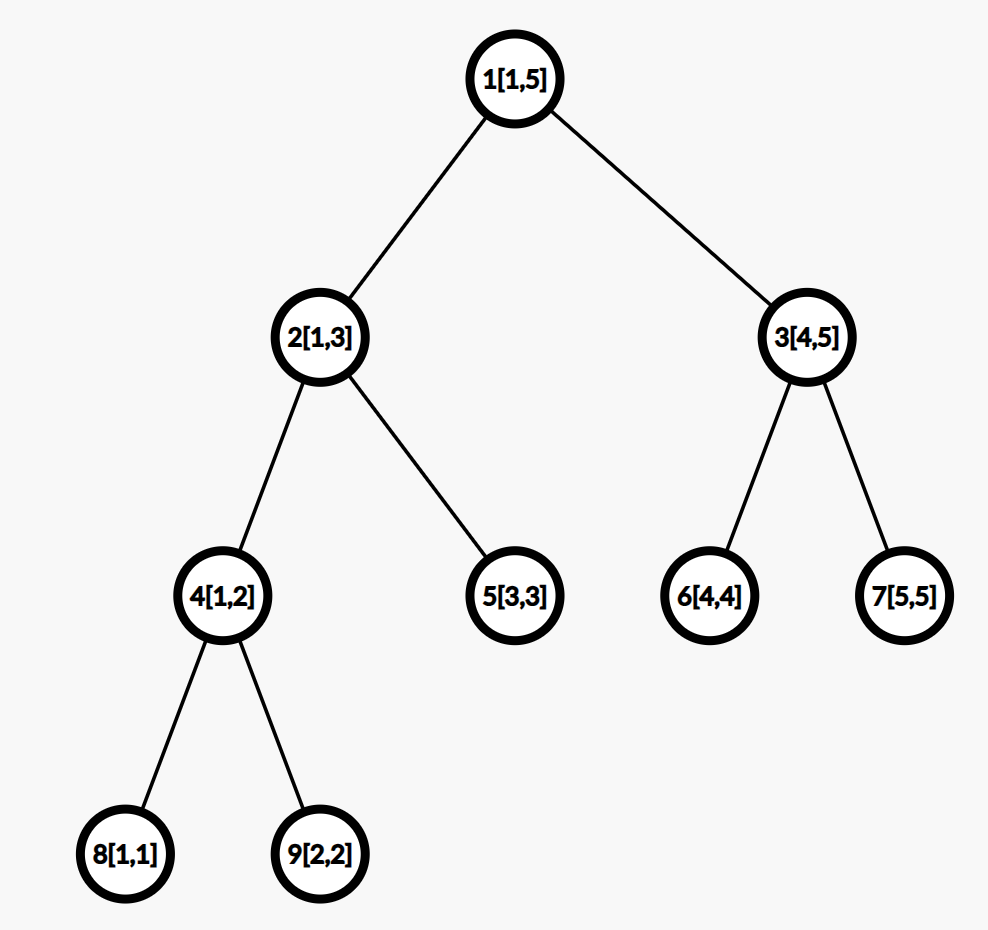
大致思想：最初有一个区间 $[1,n]$，对于一个出现在线段树的区间 $[l,r] (l \ne r)$，将其分为左右两个区间 $[l, \frac{l + r}{2}]$ 和 $[\frac{l + r}{2} + 1, r]$，各自处理，然后再结合左右区间更新区间信息。

区间肯定不能 $O(n^2)$ 记录，为了防止区间编号冲突，可以把编号为 $i$ 的节点的左儿子编号设为 $2 \times i$，右儿子编号设为 $2 \times i + 1$。

空间分析

现在有一个问题：编号最大为多少？

通过观察，容易发现线段树深度为 $\left\lceil \log n \right\rceil$，则编号最大为 $2 ^ {\left\lceil \log n \right\rceil + 1} - 1$，稍加计算可得编号不超过 $4 \times n$。

详细证明请右转 OI-wiki。

Code

int n, a[N], tr[4 * N];

// Make Tree 建树
void MT (int id, int l, int r) { // 当前节点编号为 id，区间范围 [l, r]
  if (l == r) {
    tr[id] = a[l];
    return ;
  }
  int mid = (l + r) >> 1;
  MT(id * 2, l, mid), MT(id * 2 + 1, mid + 1, r);
  tr[id] = tr[id * 2] + tr[id * 2 + 1];
}

复杂度 $O(n)$。

区间查询

对于上面的例子，我们现在需要查询某些区间的和。

如果是查询 $[1,5]$，很明显，$d_1$ 即可，可要是要求 $[2,5]$ 的怎么办呢?

既然 $[2,5]$ 并没有直接出现，那么考虑将其分为若干个出现在线段树上的区间进行求解。

大致做法

如果当前遍历到的区间 $id[l,r]$ 被查询区间完全包含，那么可以直接计算当前区间对答案的贡献，即 $d_{id}$。
如果当前遍历到的区间 $id[l,r]$ 与查询区间无交集，直接 return ;
否则，将其分为左右两个区间进行查询，即查询 $id \times 2 [l, \frac{l + r}{2}]$ 和 $id \times 2 + 1 [\frac{l + r}{2} + 1, r]$。

时间复杂度分析

做法了解了，接下来就是分析时间复杂度了。

我们可以把 $[l,r]$ 分成 $[l,l], [l+1,l+1], [l+2,l+2], \cdots [r-1,r-1],[r,r]$，尽量合并。

由于查询是一段连续区间，所以当你把所有可以合并的区间都合并之后，线段树每层最多只会有两个区间，时间复杂度为 $O(\log n)$。

Code

int qry;

// Query 查询
void Query (int id, int l, int r, int x, int y) { // 查询区间 [x, y]
  if (l >= x && r <= y) { // 当前区间被查询区间完全包含
    qry += tr[id];
    return ;
  }
  if (l > y || r < x) { // 当前区间与查询区间无交集
    return ;
  }
  int mid = (l + r) >> 1;
  Query(id * 2, l, mid, x, y), Query(id * 2 + 1, mid + 1, r, x, y);
}

单点修改

继续使用上面的例子，如果我们要修改 $a_2$ 为 $13$，该如何更新线段树呢？

如图，当你找到区间 $[2,2]$ 对应线段树上哪个节点时，你可以直接将其修改，然后再从下往上重新更新线段树每个节点即可，时间复杂度 $O(\log n)$。

如何寻找区间对应节点呢？当我们考虑到一个包含修改目标的区间 $id[l,r](l \ne r)$，很明显左右两个区间有且仅有一个区间包含修改目标，继续寻找即可，时间复杂度 $O(\log n)$。

总时间复杂度为 $O(\log n)$。

Code

// modify 单点修改
void modify (int id, int l, int r, int x, int y) { // 将 a[x] 修改为 y
  if (l == r) { // 找到修改目标
    tr[id] = y; // 直接修改
    return ;
  }
  int mid = (l + r) >> 1;
  if (mid >= x) { // 修改目标在左半区间
    modify(id * 2, l, mid, x, y);
  } else { // 修改目标在右半区间
    modify(id * 2 + 1, mid + 1, r, x, y);
  }
  tr[id] = tr[id * 2] + tr[id * 2 + 1]; // 重新更新
}

区间修改与懒标记

单点修改解决，然后就是区间修改。如果对于区间内每个元素都进行一次单点修改，时间复杂度无法接受，需要使用懒标记。

懒标记 lazy tag

懒标记~~，顾名思义就是一种十分懒惰的标记~~，用于临时记录区间操作对于当前节点对应范围造成的影响，当它要访问它的左右儿子时，需要将懒标记下传并更新左右儿子的节点信息，懒标记初始为 $0$。

引入懒标记，初始状态：

\[\texttt{(上图来源 OI-wiki)} \]

懒标记下传 Code

int lzy[4 * N];

// 将 id[l, r] 的懒标记下传
void pushdown (int id, int l, int r) {
  int mid = (l + r) >> 1;
  tr[id * 2] += lzy[id] * (mid - l + 1); // 左区间 tr 更新
  tr[id * 2 + 1] += lzy[id] * (r - mid); // 右区间 tr 更新
  lzy[id * 2] += lzy[id]; // 左区间 lazy tag 更新
  lzy[id * 2 + 1] += lzy[id]; // 右区间 lazy tag 更新
  lzy[id] = 0; // 清空当前节点 lazy tag
}

有了懒标记，我们就可以实现 $O(\log n)$ 的区间修改了。

\[\texttt{把 a 中 [3, 5] 每个元素加 5(上图来源 OI-wiki)} \]

操作类似区间查询(将区间 $[x,y]$ 每个元素增加 $z$)：

如果当前遍历到的区间 $id[l,r]$ 被修改区间完全包含，则更新当前节点的懒标记($t_{id} += z$)和答案($d_{id} += z \times (r - l + 1)$)。
如果当前遍历到的区间 $id[l,r]$ 与修改区间无交集，直接 return ;
否则，将其分为左右两个区间各自修改，即修改 $id \times 2 [l, \frac{l + r}{2}]$ 和 $id \times 2 + 1 [\frac{l + r}{2} + 1, r]$。

区间修改（加） Code

// modify 区间修改-加
void modify (int id, int l, int r, int x, int y, int z) { // 将 a[x ~ y] 每个元素加 z
  if (l >= x && r <= y) { // 当前区间被修改区间完全包含
    lzy[id] += z, tr[id] += (r - l + 1) * z;
    return ;
  }
  if (l > y || r < x) { // 当前区间与修改区间无交集
    return ;
  }
  int mid = (l + r) >> 1;
  pushdown(id, l, r); // 懒标记下传
  modify(id * 2, l, mid, x, y, z), modify(id * 2 + 1, mid + 1, r, x, y, z);
  tr[id] = tr[id * 2] + tr[id * 2 + 1]; // 重新更新当前节点
}

区间修改（赋值） Code

容易发现，一个数只与最后一次对它的赋值操作有关。所以懒标记下传与更新需要一点点的更改。

// 将 id[l, r] 的懒标记下传
void pushdown (int id, int l, int r) {
  int mid = (l + r) >> 1;
  tr[id * 2] = lzy[id] * (mid - l + 1); // 左区间 tr 更新
  tr[id * 2 + 1] = lzy[id] * (r - mid); // 右区间 tr 更新
  lzy[id * 2] = lzy[id]; // 左区间 lazy tag 更新
  lzy[id * 2 + 1] = lzy[id]; // 右区间 lazy tag 更新
  lzy[id] = 0; // 清空当前节点 lazy tag
}

// modify 区间修改-赋值
void modify (int id, int l, int r, int x, int y, int z) { // 将 a[x ~ y] 每个元素赋值为 z
  if (l >= x && r <= y) { // 当前区间被修改区间完全包含
    lzy[id] = z, tr[id] = (r - l + 1) * z;
    return ;
  }
  if (l > y || r < x) { // 当前区间与修改区间无交集
    return ;
  }
  int mid = (l + r) >> 1;
  pushdown(id, l, r); // 懒标记下传
  modify(id * 2, l, mid, x, y, z), modify(id * 2 + 1, mid + 1, r, x, y, z);
  tr[id] = tr[id * 2] + tr[id * 2 + 1]; // 重新更新当前节点
}

老师做的视频

推销一下：

优化

叶子节点没有儿子，所以懒标记不用下传到叶子节点。
根据儿子更新当前节点的操作可以写一个函数 pushup，增加代码可读性。
标记永久化：在确定懒标记不会发生溢出的情况下，可以选择不清空懒标记，只计算对答案的贡献(用处不大，主要用于可持久化数据结构)。
动态开点：左右儿子不设为 $id \times 2$ 和 $id \times 2 + 1$，而是设为线段树中没有出现的最小 $id$。线段树第一层节点数最多为 $1$，第二层最多为 $2$，第三层最多为 $4$，依次类推，可以计算出节点数量最多为 $2 \times n - 1$，可以节省空间。

$$\texttt{树状数组}$$

OI-wiki Link

树状数组，是一种用于维护单点修改和区间查询的数据结构。

一些要求

普通树状数组要求维护的信息和运算满足结合律且可差分(具有逆运算)，包括加法、乘法、异或等。

注意：

模意义下乘法若要可差分，需要保证每个元素都存在逆元。
区间极值、最大公因数等无法用普通树状数组维护(但有办法解决，详见 OI-wiki)。

初步感知

假设现在有一个数组 $a$，如果我们要求 $\sum\limits_{1\leqslant i \leqslant 7} a_i$，很明显是算 $a_1$ 到 $a_7$ 这七个数的和，那如果令 $A = a_1 + a_2 + a_3 + a_4$，$B = a_5 + a_6$，$C = a_7$，那么你肯定会说答案就是 $A+B+C$。

这就是树状数组，可以在预处理出一些区间的和之后，把一段前缀化为不超过 $\log n$ 个预处理过的区间，以 $O(\log n)$ 的方式求出前缀和。

\[\texttt{(上图来源 OI-wiki)} \]

上图中的 $c$ 数组用于存储数组 $a$ 的某些区间的和，可以发现 $c_i$ 的右端点为 $i$，可左端点呢？

区间管辖范围

树状数组规定：右端点为 $i$ 的区间的大小为 $2^{k_i}$，其中 $k$ 表示 $i$ 在二进制表示下最低位的 $1$ 的位数(最低位位数为 $0$)。

令 lowbit(i) 为 $2^{k_i}$，那么根据位运算知识，我们可以知道 lowbit(x) = x & (-x)，这个东西和原、反、补码有关，这里就不详说了，具体可以看 OI-wiki。

构建树状数组

强调：必须确保维护的信息是可差分的，例如求区间和，而区间极值则不可以用树状数组进行维护。

现在给定一个大小为 $n$ 的数组 $a$，要维护区间和，怎么构建树状数组呢？

可以想到一种比较简单的方法：对于每个 $1\leqslant i \leqslant n$，求一下 $\sum\limits_{i-lowbit(i)+1\leqslant j \leqslant i} a_i$，那么时间复杂度为多少呢？

通过找规律，可以发现这个的时间复杂度在 $n=10^7$ 也只是来到了 $12\times n$ 左右，甚至达不到 $n\log n$，也就是说，在正常情况下是完全可以通过的。

验证 Code

#include <iostream>

using namespace std;

int lowbit (int x) {
  return x & -x;
}

int n, ans;

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++) {
    ans += lowbit(i);
  }
  cout << ans;
  return 0;
}

Code

void MT () {
  for (int i = 1; i <= n; i++) {
    for (int j = i - lowbit(i) + 1; j <= i; j++) { // 统计范围内的整数和
      tr[i] += a[j];
    }
  }
}

当然如果你提前用前缀和进行预处理的话，可以直接 $O(n)$ 解决。

区间查询

举个例子，现在要求区间 $[3, 5]$ 的和，那么就可以将其分为两个前缀 $[1,5]$ 和 $[1,2]$ 分别进行求解，然后做差(前缀和思想)。

根据区间管辖范围，我们可以轻松地推出前缀和的求法：函数 Query(x) 求解的是前缀 $[1,x]$ 的和，先算上以 $x$ 结尾的区间和 $c_x$，求解范围为 $[x - lowbit(x) + 1,x]$，也就是说还差 $[1,x - lowbit(x)]$ 没有求解，也就是 Query(x - lowbit(x))，如果现在 x = 0，即已将前缀完全求解，那么直接返回 $0$ 即可。

\[Query(x)=\begin{cases}0&x=0\\c_x+Query(x-lowbit(x))&x\geqslant 1\end{cases} \]

Code

inline int lowbit (int x) {
  return x & -x; // 位运算求 lowbit
}

int n, tr[N]; // tr 就是 c 数组

int Query (int x) {
  return (x ? tr[x] + Query(x - lowbit(x)) : 0); // 分类讨论
}

单点修改

树状数组の一些性质

令 $l_x$ 为 $x - lowbit(x) + 1$。

对于任意 $x \leqslant y$，要么 $l_y > x$，要么 $l_y \leqslant l_x$。
对于任意 $x$，有 $l_{x+lowbit(x)} \leqslant l_x$。
对于任意 $x < y < x + lowbit(x)$，有 $l_y > x$。

详细证明见 OI-wiki。

假设现在要将 $a_x$ 加上 $y$。

为了快速更新 $c$，我们只需要更新所有包含 $x$ 的 $c$ 即可。

根据如上几个性质，可以推出更新方法：当 $c_a$ 包含 $x$ 时，更新 $c_a$，并更新 $c_{a + lowbit(a)}$，以此类推，直到 $a > n$，此时也就是更新完毕了，很明显 $c_x$ 是一定包含 $x$ 的。

Code

void modify (int x, int y) { // 单点修改
  if (x > n) { // 更新完毕
    return ; // 返回
  }
  tr[x] += y, modify(x + lowbit(x), y); // 更新
}

复杂度 $O(\log n)$。

区间修改

开两个树状数组，利用差分维护即可。

posted @ 2023-08-18 23:07 wnsyou 阅读(49) 评论(0) 编辑收藏举报

刷新页面返回顶部

wnsyou の blog

线段树与树状数组

$$\texttt{线段树}$$

基本结构

空间分析

Code

区间查询

大致做法

时间复杂度分析

Code

单点修改

Code

区间修改与懒标记

懒标记 lazy tag

懒标记下传 Code

区间修改（加） Code

区间修改（赋值） Code

老师做的视频

优化

$$\texttt{树状数组}$$

一些要求

初步感知

区间管辖范围

构建树状数组

验证 Code

Code

区间查询

Code

单点修改

树状数组の一些性质

Code

区间修改

公告