组合数学
排列组合
排列组合是组合数学的基础，排列就是取出部分数字进行排序，组合就是不考虑顺序。
排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。
加法、乘法原理
加法原理：一个东西有 \(n\) 类办法，第 \(i\) 类办法分 \(a_i\) 种，总共就有 \(\sum\limits_{1\leqslant i \leqslant n}a_i\) 种。
乘法原理：一个东西有 \(n\) 个步骤，第 \(i\) 步有 \(a_i\) 种方法，总共就有 \(\prod\limits_{1\leqslant i \leqslant n} a_i\) 种。
排列数与组合数
排列数，代表的是从 \(n\) 个数中任选 \(m\) 个元素在考虑顺序的情况下有多少种情况。
排列数的公式：\(A_n^m=n\times (n-1)\times (n-2)\cdots \times(n-m+1)=\frac{n!}{(n-m)!}\)。
组合数也差不多，但是不考虑顺序。
组合数的公式：\(\begin{pmatrix}n\\m\end{pmatrix}=C_n^m= \frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}\)。
tips:组合数也被称为「二项式系数」。
组合数求解-帕斯卡公式
\(C_n^m=C_n^{m-1}+C_{n-1}^{m-1}\)。
组合数求解-预处理逆元
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7;
int n, inv[N], X[N], F[N];
inline int C (int a, int b) {
return (a >= b ? 1ll * F[a] * X[b] % mod * X[a - b] % mod : 0);
}
inline int A (int a, int b) {
return (a >= b ? 1ll * F[a] * X[a - b] % mod : 0);
}
int main () {
ios::sync_with_stdio(0), cin.tie(0);
inv[1] = X[0] = F[0] = 1;
for (int i = 2; i <= n; i++)
inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
for (int i = 1; i <= n; i++)
X[i] = 1ll * X[i - 1] * inv[i] % mod, F[i] = 1ll * F[i - 1] * i % mod;
return 0;
}
二项式定理
\((x+y)^n=\sum\limits_{i=0}\limits^{n} C_n^i x ^{n-i}y^i\)。
卢卡斯定理
卢卡斯定理可以求大数的 \(C_n^m \mod p\)。
对于非负整数 \(n,m\)，\(C_n^m \equiv C_{n\mod p}^{m\mod p}\times C_{\frac{n}{p}}^{\frac{m}{p}} \pmod p\)。
递归实现即可。
int lucas (int n, int m) {
return (!m ? 1 : 1ll * lucas(n / mod, m / mod) * C(n % mod, m % mod) % mod);
}
多重集排列
有一个多重集，元素种类为 \(n\)，第 \(i\) 个元素有 \(a_i\) 个。
那么多重集的 \(n\) 排列数为 \(\frac{n!}{\prod\limits_{1\leqslant i\leqslant n} a_i}\)。
多重集的 \(r\) 组合数就是 \(C_{n - 1}^{r+n-1}\)。
抽屉(鸽巢)原理
鸽巢(the pigeonhole principle)原理，通常用于求解一些比较极端的情况。
最基础：如果有 \(n+1\) 个物品放入 \(n\) 个抽屉里，至少有 \(1\) 个抽屉至少有 \(2\) 个物品(反证法)。
进阶：如果有 \(k\) 个物品放入 \(n\) 个抽屉里，至少有 \(1\) 个抽屉至少有 \(\left\lceil \frac{k}{n} \right\rceil\)。
容斥原理
容斥原理的思想大致就是在求总量时，可以先不管重不重复，求出总和后再减去重复部分。
二元容斥：\(|A\cup B|=|A|+|B|-|A\cap B|\)。
三元容斥：\(|A\cup B \cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B \cap C|\)。
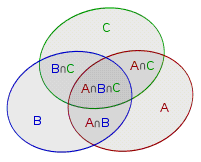
把它推广一下就是我们熟知的容斥原理了。
卡特兰数 Catalan
卡特兰数 \(H_n\) 可以求解以下问题：
- 长度为 \(2n\) 的合法括号序列的个数。
- 在圆上选择 \(2n\) 个点，将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的方法数。
- ......
求解式：
- \(H_i=\frac{C_{2n}^n}{n+1}\)。
- \(H_i=\begin{cases} \sum\limits_{0\leqslant j < i} H_j\times H_{i-j-1}&i>0\\ 0&i=0\end{cases}\)。
- \(H_i=\begin{cases} \frac{4n-2}{n+1}\times H_{i-1} &i>0\\ 0&i=0\end{cases}\)。
