字符串进阶(自动机,失配树)
$$\texttt{自动机}$$
自动机的引入
自动机是一个数学模型,不是算法也不是数据结构。OI 所说的「自动机」一般都指「确定有限状态自动机(DFA)」。
自动机的工作方式和流程图类似,不同的是:自动机的每一个结点都是一个判定结点;自动机的结点只是一个单纯的状态而非任务;自动机的边可以接受多种字符。
例如:用自动机解决判断二进制数是否为偶数时,你可以从高位往低位处理,根据每一位是 \(0\) 还是 \(1\) 处理答案
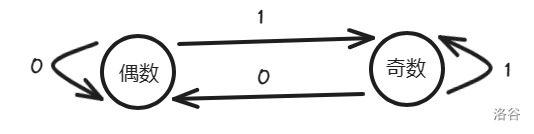
\[\texttt{判断二进制数是否为偶数的自动机}
\]
在某些情况下看起来挺废物的作用不明显,但处理一些特定问题时会很方便。
自动机的形式化定义
- 字符集(\(\sum\)):非常重要,自动机只能处理这些字符,要仔细读题。
- 状态集合(\(Q\)):如果将 DFA 看作一张有向图,那么 DFA 的状态就是图上的节点。
- 起始状态(\(s\)):自动机的初始状态,例如上文的自动机起始状态就是偶数。
- 接受状态集合(\(F\)):特殊的状态,详细见下文。
- 转移函数(\(\delta\)):非常重要,它接受一个状态和字符集内的一个字符,返回一个状态。
当 DFA 读入一个字符串时,其会从起始状态开始按照转移函数一个个地处理字符转移。若读入完一个字符串后停留的状态属于接受状态集合,则称 DFA 接受这个字符串,否则成为 DFA 不接受这个字符串。
若一个状态 \(v\) 没有字符 \(c\) 的转移,则 \(\delta(v,c)=null\),\(null\) 只能转移到 \(null\),且 \(null\) 不属于接受状态集合。简而言之,\(null\) 代指所有无法转移到任何一个接受状态的状态。
例如一个只接受字符串 a,ab 和 aac 的 DFA如下:
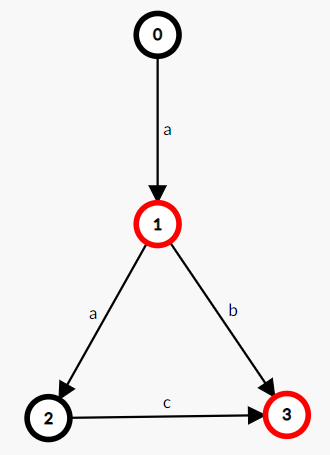
\[\texttt{(图片来源于 OI-wiki)红色节点代表接受状态}
\]
KMP 自动机
快速回顾:KMP。
nxt[0][t[1] - 'A'] = 1;
for (int i = 1; i <= m; i++) {
for (int j = 0; j < 26; j++) {
if (i < m && j + 'A' == t[i + 1]) {
nxt[i][j] = i + 1, p[i + 1] = nxt[p[i]][j];
} else {
nxt[i][j] = nxt[p[i]][j];
}
}
}
$$\texttt{失配树}$$
快速回顾:失配树。
失配树,即一棵利用失配数组建出来的树,树上一个节点 \(i\) 的父亲为 \(nxt_{i}\)。
性质
- 树上的两个节点 \(x,y\) 的 LCA 就是 \(pre(s,x)\) 和 \(pre(s,y)\) 的最长公共 Border。
- 一个前缀的所有 Border 都对应其在失配树上的一个祖先节点。
- 一个前缀在串中每一次出现都对应其在失配树上的节点的子树范围内的一个节点。
习题
模板题:P5829 【模板】失配树。
习题:CF432D Prefixes and Suffixes(利用性质 \(3\)) | P2375 动物园(利用性质 \(2\),倍增查找)


