abc269_f Numbered Checker 题解

合集 - 题解(48)

1.CSES 1667 Message Route 题解2023-02-132.P3956 棋盘 题解2023-02-223.abc233_f Swap and Sort 题解2023-03-034.abc233_e Σ[k=0..10^100]floor(X／10^k) 题解2023-03-035.abc233_d Interval 题解2023-03-036.abc233_c Product 题解2023-03-017.abc249_f Ignore Operations 题解2023-04-168.abc249_d Index Trio 题解2023-04-169.abc248_e K-colinear Line 题解2023-04-1310.abc247_f Cards 题解2023-04-1211.CF1066C Books Queries 题解2023-03-1412.P1038 神经网络 题解2023-03-1413.SeekLuna P1362 拓扑排序 3 题解2023-03-1414.abc232_e Rook Path 题解2023-03-0315.abc235_e MST + 1 题解2023-05-1716.abc234_e Arithmetic Number 题解2023-05-1717.P8786 李白打酒加强版 题解2023-05-1718.abc235_d Multiply and Rotate 题解2023-05-1719.CF1095D Circular Dance 题解2023-05-1720.P6201 & P1985 Fliptile S 题解2023-05-1721.CF1183C Computer Game 题解2023-05-1722.CF1095E Almost Regular Bracket Sequence 题解2023-05-1723.abc256_e Takahashi's Anguish 题解2023-05-1724.abc260_g Scalene Triangle Area 题解2023-05-1625.P8714 填空问题 题解2023-05-0926.abc252_d Distinct Trio 题解2023-04-2927.abc252_f Bread 题解2023-04-2328.abc253_e Distance Sequence 题解2023-04-2329.abc250_e Prefix Equality 题解2023-04-1630.abc250_d 250-like Number 题解2023-04-1631.arc164_a Ternary Decomposition 题解2023-07-1232.abc275_f Erase Subarrays 题解2023-06-0233.abc275_e Sugoroku 4 题解2023-05-3134.abc274_d Robot Arms 2 题解2023-05-3135.abc260_f Find 4-cycle 题解2023-05-2436.abc260_e At Least One 题解2023-05-2437.abc273_e Notebook 题解2023-05-2438.abc271_f XOR on Grid Path 题解2023-05-2439.abc271_e Subsequence Path 题解2023-05-2240.abc271_c Manga 题解2023-05-22

41.abc269_f Numbered Checker 题解2023-05-18

42.abc270_f Transportation 题解2023-05-1743.CF1077E Thematic Contests 题解2023-05-1744.CF1935D Exam in MAC 题解2024-04-0145.CF1144G Two Merged Sequences 题解2024-06-1546.joi2022_yo2_c 国土分割 (Land Division) 题解2024-07-0947.P3588 PUS 题解2024-07-2048.CF1946F Nobody is needed 题解2024-08-03

收起

Numbered Checker

题意

有一个 $n\times m$ 的方格矩阵，左上角是 $(1,1)$，右下角是 $(n,m)$，每个方格中都有一个整数，其中 $(x,y)$ 中的数字为：

• 如果 $x+y$ 是奇数，则 $(x,y)$ 中的数字为 $0$。
• 否则，$(x,y)$ 中的数字为 $(x-1)\times m+y$。

有 $Q$ 组询问，每组询问给定四个整数 $a,b,c,d$，求所有满足要求的 $(i,j)$ 中的数字之和：

• $a⩽i⩽b$。
• $c⩽j⩽d$。

答案对 $998244353$ 取模。

思路

等差数列求和。

对于每组询问

暴力时间复杂度：$O(n\times m)$，爆炸。

推导壹

就拿第一个样例举例子。

可以很明显地发现，奇数行与偶数行排列虽然不太一样，但两者都是等差数列，且公差为 $2$。

经过仔细地推导(不给推导过程，自己推去)，我们可以发现：

• 对于 $a+c$ 为奇数的情况下：
  • 第 $a$ 行的等差数列首项为 $(a,c+1)$，项数为 $\frac{d-c+1}{2}$。
  • 第 $a+1$ 行的等差数列首项为 $(a+1,c)$，项数为 $1+\frac{d-c}{2}$。
• 对于 $a+c$​ 为偶数的情况下：
  • 第 $a$ 行的等差数列首项为 $(a,c)$，项数为 $\frac{d-c}{2}+1$。
  • 第 $a+1$ 行的等差数列首项为 $(a+1,c+1)$，项数为 $\frac{d-c+1}{2}$。

(以上除法均需带有向下取整)。

时间复杂度：$O(n)$，还是不够优秀。

推导贰

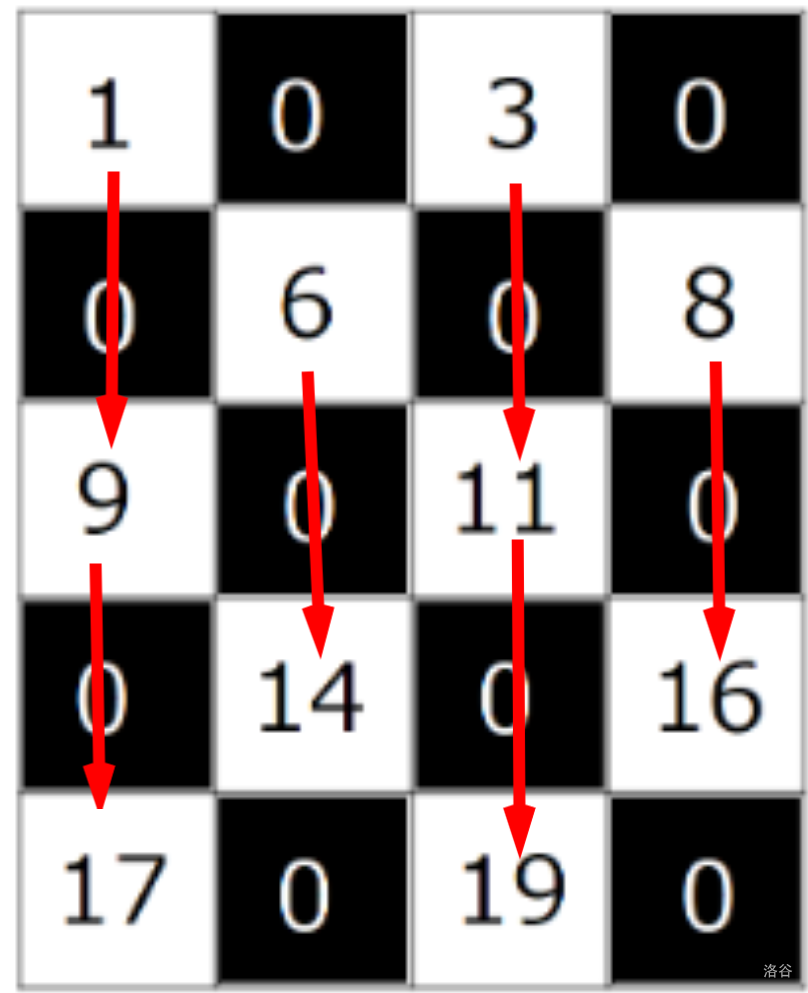
可以发现，行与行之间也是等差数列！公差为 $2m$。

令当前询问第 $a$ 行的等差数列之和为 $sum$，项数为 $p$；第 $a+1$ 行的等差数列之和为 $num$，项数为 $q$。

还是不给推导过程，答案就可以变成两个等差数列：

• 第一个：以 $sum$ 为首项，公差为 $2\times m\times p$，项数为 $\frac{b-a}{2}+1$。
• 第二个：以 $num$ 为首项，公差为 $2\times m\times q$，项数为 $\frac{b-a+1}{2}$。

求出两个等差数列之和，将其加起来就是答案啦，注意取模细节。

时间复杂度：$O(1)$。

复杂度

• 时间：$O(Q)$。
• 空间：$O(1)$。

Code

点击查看代码

#include <iostream>
 
using namespace std;
using ll = long long;
 
const int mod = 998244353;
 
ll n, m, t, a, b, c, d, p, q, sum, num;
 
ll id (ll x, ll y) { // 将坐标转数值
  return ((x - 1) * m + y) % mod;
}
 
ll Sum (ll s, ll d, ll n) { // 等差数列求和公式
  return (s * n + n * (n - 1) / 2 % mod * d % mod) % mod;
}
 
int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  for (cin >> n >> m >> t; t; t--) {
    cin >> a >> b >> c >> d;
    p = (d - c + 1) / 2, q = (d - c) / 2 + 1;
    if ((a + c) % 2) {
      sum = Sum(id(a, c + 1), 2, p), num = Sum(id(a + 1, c), 2, q); // 套用公式
    } else {
      swap(p, q);
      sum = Sum(id(a, c), 2, p), num = Sum(id(a + 1, c + 1), 2, q);
    }
    cout << (Sum(sum, 2 * m * p % mod, (b - a) / 2 + 1) + Sum(num, 2 * m * q % mod, (b - a + 1) / 2)) % mod << '\n'; // 各种取模细节
  }
  return 0;
}