CF1095E Almost Regular Bracket Sequence 题解

Almost Regular Bracket Sequence

题意

有一个长度为 \(n\) 的括号序列。

求有多少个位置使得改变了该位置的括号种类可以使得括号序列合法。

思路

令左括号为 \(1\)，右括号为 \(-1\)，且这个序列所有数之和为 \(x\)。

首先分为三种情况。

1. \(x = 2\)，那么说明左括号多了一个（一个右括号变一个左括号会使得 \(x\) 减少 \(2\)），要选择一个左括号变成右括号。
2. \(x = -2\)，那么说明右括号多了一个，要选择一个右括号变成左括号。
3. \(x < -2\) 或 \(x > 2\) 或 \(-2 < x < 2\)，答案必将为 \(0\)，可以直接输出。

对于情况一

设前 \(i\) 个括号序列的和为 \(sum_i\)。

首先，我们来观察一个图：

在这种情况里，虽然 \(x = 2\)，但是仍然没有答案。Why？

合法的括号序列，有一个条件，那就是在任何时候，左括号的数量都不能比右括号少！

所以，我们可以推出第一个条件：

• 可以作为答案的位置 \(i\) 必然要满足 \(\sum\limits_{1 \leqslant j < i}{(sum_ j\geqslant 0)} = i - 1\)

那么，当我们第一次发现 \(sum_{i-1} < 0\) 时，就可以退出找答案的循环了，后面的所有位置均不可成为答案。

再来观察一个图：

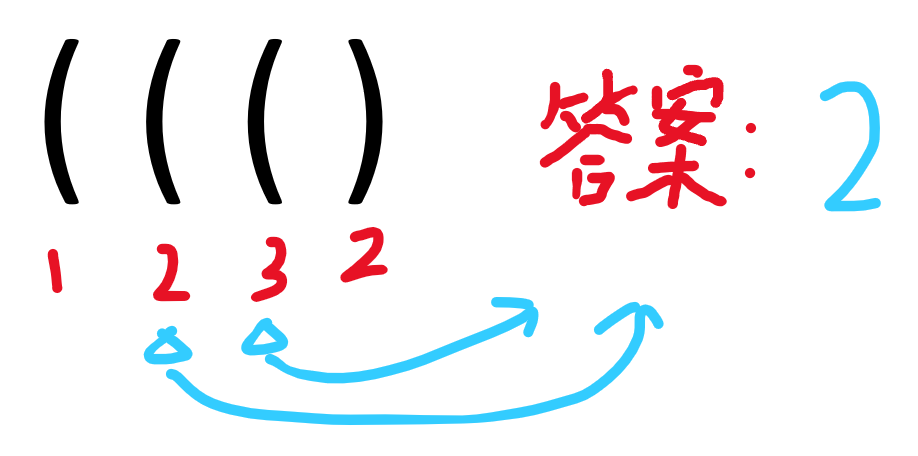
位置 \(2\) 和位置 \(3\) 给答案有贡献，那为啥位置 \(1\) 没有贡献呢？

虽然我们知道，位置 \(1\) 一旦变化，就会出现 \(sum_1 = -1\) 的情况，可究竟怎样筛掉这些情况呢？

手推一下，我们会发现：把位置 \(i\) 上的左括号变为右括号，会使得 \(sum_j-2\ (j \geqslant i)\)。

那么就好办了，只要 \(\min\limits_{i \leqslant j \leqslant n}\{sum_j\} \geqslant 2\) 且位置 \(i\) 为左括号，这个位置即可对答案产生贡献。

对于情况二

同理，只要 \(\min\limits_{i \leqslant j \leqslant n}\{sum_j\} \geqslant -2\) 且位置 \(i\) 为右括号，这个位置即可对答案产生贡献。

总结

• 如果 \(\left\vert x \right\vert \neq 2\)，答案必为 \(0\)。
• 如果 \(x = 2\)，答案为满足要求的 \(i\) 的个数。
  • \(s_i = (\)。
  • \(\sum\limits_{1 \leqslant j < i}{(sum_ j\geqslant 0)} = i - 1\) 且 \(\min\limits_{i \leqslant j \leqslant n}\{sum_j\} \geqslant 2\)。
• 如果 \(x = -2\)，答案为满足要求的 \(i\) 的个数。
  • \(s_i = )\)。
  • \(\sum\limits_{1 \leqslant j < i}{(sum_ j\geqslant 0)} = i - 1\) 且 \(\min\limits_{i \leqslant j \leqslant n}\{sum_j\} \geqslant -2\)。

用前缀和思想处理出 \(sum\) 数组，再求一遍 \(sum\) 的后缀最小值，统计答案即可。

Code

点击查看代码

#include <iostream>
#include <string>

using namespace std;

const int N = 1e6 + 10;

string s;
int n, sum[N], mi[N], ans; // sum 为前缀和，mi 为 sum 的后缀最小值

int main () {
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> s;
  for (int i = 1; i <= n; i++) {
    sum[i] = sum[i - 1];
    if (s[i - 1] == '(') { // 处理好前缀和
      sum[i]++;
    } else {
      sum[i]--;
    }
  }
  mi[n] = sum[n];
  for (int i = n - 1; i; i--) { // 处理后缀最小值
    mi[i] = min(mi[i + 1], sum[i]);
  }
  for (int i = 1; i <= n; i++) {
    if (sum[n] == 2 && mi[i] >= 2 && s[i - 1] == '(') { // 判断，情况 1
      ans++;
    } else if (sum[n] == -2 && mi[i] >= -2 && s[i - 1] == ')') { // 判断，情况 2
      ans++;
    }
    if (sum[i] < 0) { // 处理 i + 1 时，sum[i] < 0，结束循环
      break;
    }
  }
  cout << ans;
  return 0;
}