P8714 填空问题 题解
填空问题
题意
自己看（
思路
分五个小题去考虑。
问题 A
枚举门牌号，看门牌号中有多少个 \(2\)，统计答案即可。
点击查看代码
void SolveA () { // 问题 A
int sum = 0;
for (int i = 1, j; i <= 2020; i++) { // 枚举门牌号
j = i;
while (j) { // 枚举每一位
sum += (j % 10 == 2); // 统计 2 的数量
j /= 10;
}
}
cout << sum;
}
输出答案：\(624\)。
问题 B
枚举分子和分母，判断分子分母是否互质，统计互质的分子分母对数。
点击查看代码
int gcd (int x, int y) { // 欧几里得算法求最小公因数
return (y ? gcd(y, x % y) : x);
}
void SolveB () { // 问题 B
int sum = 0;
for (int i = 1; i <= 2020; i++) {
for (int j = 1; j <= 2020; j++) { // 先枚举分子分母
sum += (gcd(i, j) == 1); // 判断是否互质
}
}
cout << sum;
}
输出答案：\(2481215\)。
问题 C
开始有难度了哟。
首先画一个草图：
经过观察，我们可以发现：对于每个整数 \(x\)，位于 \((x,x)\) 的数所在的红线箭头都是从下往上的。
那么答案要求的那个数必然也在一条从下往上的红线上。
再观察一下，贯穿 \((x,x)\) 的红线起始点在 \((2x - 1,1)\) 上。
再推一下，假设我们现在求的是位于 \((3,3)\) 的数，可以发现：
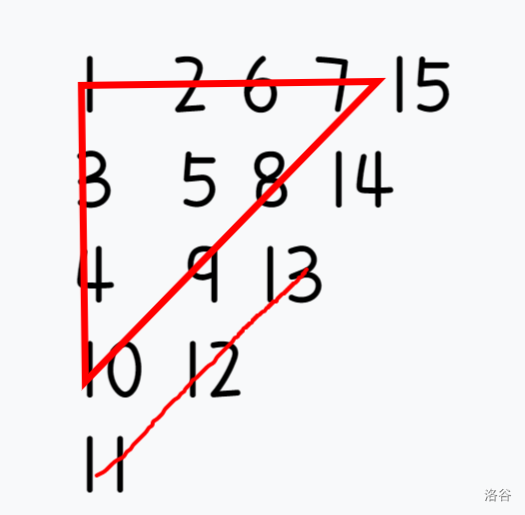
这里有一个三角形，三角形中的数的个数再加上 \(x\) 就是答案！三角形中的数的个数也很好求，就是 \(1 + 2 + 3 + \cdots + (2x - 2)\)。
综上所述，求位于 \((x,x)\) 的数的公式就是 \((1 + 2x - 2) \times (2x - 2) / 2 + x\)。
点击查看代码
void SolveC () { // 问题 C
int x = 20 * 2 - 1;
cout << (x * (x - 1) / 2 + 20); // 套用公式
}
输出答案：\(761\)。
问题 D
模拟一下，有些细节，处理号闰年和星期等问题就行了。具体看代码。
点击查看代码
const int D[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; // 每一个月的天数
bool leap (int y) { // 判断闰年，如果是闰年则返回值为 1，否则返回值为 0
if (y % 100) { // 不是整百年
return !(y % 100 % 4);
}
y /= 100; // 是整百年
return !(y % 4);
}
bool check (int y, int m, int d) { // 判断是否已经求完了所有日子。
return !(y == 2020 && m == 10 && d == 2); // 因为包含了 2020.10.1，所以要往后一天
}
void SolveD () { // 问题 D
int y = 2000, m = 1, d = 1, z = 6, ans = 0; // y 为年份，m 为月份，d 为日期，z 为星期几，ans 为答案
while (check(y, m, d)) { // 判断
ans++; // 每天至少跑 1 km
if (z == 1 || d == 1) { // 特殊日子
ans++; // 再跑 1 km
}
d++, z = z % 7 + 1; // 处理日期变更
if (m != 2 || !leap(y)) { // 不是二月或不是闰年
if (d == D[m] + 1) { // 正常处理
m++, d = 1;
}
} else { // 是闰二月
if (d == 30) { // 特殊处理
m++, d = 1;
}
}
if (m == 13) { // 一年又过完了
y++, m = 1; // 新的一年！
}
}
cout << ans;
}
输出答案：\(8879\)。
问题 E
看了一下题解区，实现也没简单到哪去，枚举一下每个二极管亮或不亮，从某一个亮着的二极管开始做一次深搜，判断是否可以只通过亮着的二极管走到所有二极管。
先建一张图我蠢了用了个邻接表，可以通过枚举二进制数来方便的枚举每种情况，统计答案即可。
点击查看代码
void pret () { // 日常犯蠢 1/1
v[0].push_back(1), v[0].push_back(5);
v[1].push_back(0), v[1].push_back(2), v[1].push_back(6);
v[2].push_back(1), v[2].push_back(3), v[2].push_back(6);
v[3].push_back(2), v[3].push_back(4);
v[4].push_back(3), v[4].push_back(5), v[4].push_back(6);
v[5].push_back(0), v[5].push_back(4), v[5].push_back(6);
v[6].push_back(1), v[6].push_back(2), v[6].push_back(4), v[6].push_back(5);
}
void dfs (int x) { // 简单 dfs
if (vis[x] || !f[x]) {
return ;
}
vis[x] = 1, num++;
for (int i : v[x]) {
dfs(i);
}
}
void SolveE () { // 问题 E
int sum = 0;
pret(); // 预处理
for (int i = 1; i < (1 << 7); i++) { // 枚举二进制对应的十进制数
int st = 7, cnt = 0; // st 为任意的一个亮着的二极管，我就编号取最小的一个
num = 0;
for (int j = 0; j < 7; j++) { // 二进制拆分
f[j] = ((i >> j) & 1), vis[j] = 0;
if (f[j]) {
st = min(st, j), cnt++;
}
}
dfs(st); // 做一次深搜
sum += (num == cnt); // 如果能够找到所有发光二极管，答案加 1
}
cout << sum;
}
输出答案：\(80\)。
好了，到这里，所有小题全部解决了，总体代码 \(126\) 行，对我来说是比较长的了。
Code
点击查看完整版代码
#include <iostream>
#include <vector>
using namespace std;
const int D[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; // 每一个月的天数
char c;
vector<int> v[10];
bool vis[10], f[10];
int num;
void pret () { // 日常犯蠢 1/1
v[0].push_back(1), v[0].push_back(5);
v[1].push_back(0), v[1].push_back(2), v[1].push_back(6);
v[2].push_back(1), v[2].push_back(3), v[2].push_back(6);
v[3].push_back(2), v[3].push_back(4);
v[4].push_back(3), v[4].push_back(5), v[4].push_back(6);
v[5].push_back(0), v[5].push_back(4), v[5].push_back(6);
v[6].push_back(1), v[6].push_back(2), v[6].push_back(4), v[6].push_back(5);
}
int gcd (int x, int y) { // 欧几里得算法求最小公因数
return (y ? gcd(y, x % y) : x);
}
bool leap (int y) { // 判断闰年，如果是闰年则返回值为 1，否则返回值为 0
if (y % 100) { // 不是整百年
return !(y % 100 % 4);
}
y /= 100; // 是整百年
return !(y % 4);
}
bool check (int y, int m, int d) { // 判断是否已经求完了所有日子。
return !(y == 2020 && m == 10 && d == 2); // 因为包含了 2020.10.1，所以要往后一天
}
void dfs (int x) { // 简单 dfs
if (vis[x] || !f[x]) {
return ;
}
vis[x] = 1, num++;
for (int i : v[x]) {
dfs(i);
}
}
void SolveA () { // 问题 A
int sum = 0;
for (int i = 1, j; i <= 2020; i++) { // 枚举门牌号
j = i;
while (j) { // 枚举每一位
sum += (j % 10 == 2); // 统计 2 的数量
j /= 10;
}
}
cout << sum;
}
void SolveB () { // 问题 B
int sum = 0;
for (int i = 1; i <= 2020; i++) {
for (int j = 1; j <= 2020; j++) { // 先枚举分子分母
sum += (gcd(i, j) == 1); // 判断是否互质
}
}
cout << sum;
}
void SolveC () { // 问题 C
int x = 20 * 2 - 1;
cout << (x * (x - 1) / 2 + 20); // 套用公式
}
void SolveD () { // 问题 D
int y = 2000, m = 1, d = 1, z = 6, ans = 0; // y 为年份，m 为月份，d 为日期，z 为星期几，ans 为答案
while (check(y, m, d)) { // 判断
ans++; // 每天至少跑 1 km
if (z == 1 || d == 1) { // 特殊日子
ans++; // 再跑 1 km
}
d++, z = z % 7 + 1; // 处理日期变更
if (m != 2 || !leap(y)) { // 不是二月或不是闰年
if (d == D[m] + 1) { // 正常处理
m++, d = 1;
}
} else { // 是闰二月
if (d == 30) { // 特殊处理
m++, d = 1;
}
}
if (m == 13) { // 一年又过完了
y++, m = 1; // 新的一年！
}
}
cout << ans;
}
void SolveE () { // 问题 E
int sum = 0;
pret(); // 预处理
for (int i = 1; i < (1 << 7); i++) { // 枚举二进制对应的十进制数
int st = 7, cnt = 0; // st 为任意的一个亮着的二极管，我就编号取最小的一个
num = 0;
for (int j = 0; j < 7; j++) { // 二进制拆分
f[j] = ((i >> j) & 1), vis[j] = 0;
if (f[j]) {
st = min(st, j), cnt++;
}
}
dfs(st); // 做一次深搜
sum += (num == cnt); // 如果能够找到所有发光二极管，答案加 1
}
cout << sum;
}
int main () {
// freopen("output", "w", stdout);
ios::sync_with_stdio(0), cin.tie(0);
cin >> c;
if (c == 'A') {
SolveA();
} else if (c == 'B') {
SolveB();
} else if (c == 'C') {
SolveC();
} else if (c == 'D') {
SolveD();
} else {
SolveE();
}
return 0;
}
点击查看简略版代码
#include<iostream>
using namespace std;
int ans[5] = {624, 2481215, 761, 8879, 80};
char c;
int main() {
cin >> c;
cout << ans[c - 'A'];
return 0;
}
