P1038 神经网络 题解

神经网络

题意

有 \(n\) 个节点和 \(p\) 条边。

每个节点可以长成这样：

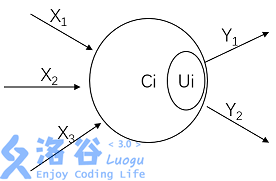
每个节点都有一个内在参数 \(u_i\)，还有一个状态 \(c_i\)。

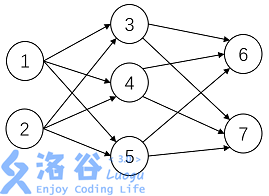
节点按照一定顺序排列，可分为三种类型：输入层，中间层和输出层，每个节点只可从上一层接受信息，向下一层传递信息。

对于每个点的状态，有以下公式：

\[c_i=\left(\sum\limits_{(j,i) \in E} w_{j,i}\times c_{j}\right)-u_{i} \]

其中 \(w_{j,i}\) 为一条从节点 \(j\) 转移到节点 \(i\) 的边上的边权。

当 \(c_i > 0\) 时，该节点可以向它连向的节点发送信号，否则就不行。

---

给定了每个节点的初始状态和内在参数，\(p\) 条有向边从 \(x_i\) 连向 \(y_i\)，边权为 \(w_{x_i,y_i}\)

不是输入层的节点初始状态一定为 \(0\)

请求出所有 \(c_i>0\) 的输出层节点的编号还有最终状态（就是 \(c_i\)），如果没有则输出 NULL

数据范围

• \(1 \leqslant n \leqslant 100\)
• 两个节点直接最多只有一条边

思路

很明显，这里不会有环和重边，拓扑序也可以轻松发现。

那么这题就是拓扑排序的天下了，在求拓扑序的同时去求一下 \(c_i\) 即可。

细节

1 公式

只有 \(c_i > 0\) 时才可以向其他点发送信号，同理也只有当 \(c_j > 0\) 时才可以从这个点接收信号

也就是说，公式可以变成这样：

\[c_i=\left(\sum\limits_{(j,i) \in E,c_j>0} w_{j,i} \times c_{j}\right)-u_{i} \]

2 逻辑

题意中有一个逻辑坑点：

不是输入层的节点初始状态一定为 \(0\)

并没有说输入层的节点初始状态一定不为 \(0\)，所以要稍加小心（只是代码逻辑问题，对答案并不能产生影响，因为输入层节点初始状态若为 \(0\)，那么也是不可以向下一层传输信号的）

3 分类

输入层的节点不参与公式计算，即不会减去内在参数。

复杂度

• 时间：\(O(n+m)\)
• 空间：\(O(n+m)\)

Code

点击查看代码

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

struct node {
  int f, u;
} a[110];
struct Node {
  int x, y;
};

int n, m, ansf, x, y, z, b[110], c[110];
vector<Node> v[110];

void dfs (int x) {
  b[x]--; // 相当于一种标记
  if (!a[x].f) { // 不是输入层
    c[x] -= a[x].u; // 减去内在参数
  }
  for (auto i : v[x]) {
    b[i.x]--;
    if (c[x] > 0) { // 只有当前点的ci>0时才可以发送信号
      c[i.x] += c[x] * i.y; // 公式套上
    }
    if (!b[i.x]) { // 这个点计算完了
      dfs(i.x); // 调用一下
    }
  }
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n >> m;
  for (int i = 1; i <= n; i++) {
    cin >> a[i].f >> a[i].u; // 初始状态和内在参数
  }
  for (int i = 1; i <= m; i++) {
    cin >> x >> y >> z;
    v[x].push_back({y, z}); // 边
    b[y]++;
  }
  for (int i = 1; i <= n; i++) {
    if (a[i].f) { // 输入层
      c[i] = a[i].f;
      dfs(i);
    }
  }
  for (int i = 1; i <= n; i++) {
    if (!v[i].size() && c[i] > 0) { // 输出层且满足要求
      cout << i << ' ' << c[i] << '\n'; // 输出一下
      ansf = 1; // 标记有答案
    }
  }
  if (!ansf) { // 没有答案，输出NULL
    cout << "NULL";
  }
  return 0;
}