一些泰勒级数
指数函数
引用 http://www.ab126.com/shuxue/3824.html
\[\begin{array}{l}
e^{x}=1+\frac{x}{1 !}+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\cdots\qquad
-\infty<x<\infty\\
e^{-x^{2}}=1-x^{2}+\frac{x^{4}}{2 !}-\frac{x^{6}}{3 !}+\frac{x^{8}}{4 !}-\cdots\qquad
-\infty<x<\infty\\
a^{x}=e^{x \ln a}=1+\frac{x \ln a}{1 !}+\frac{(x \ln a)^{2}}{2 ! a b)}+\frac{(x \ln a)^{3}}{263 ! 0 m}+\cdots \quad-\infty<x<\infty\\
e^{\sin x}=1+x+\frac{x^{2}}{2}-\frac{x^{4}}{8}-\frac{x^{5}}{15}+\cdots\qquad-\infty<x<\infty\\
e^{\cos x}=e\left(1-\frac{x^{2}}{2}+\frac{x^{4}}{6 m-\frac{31 x^{6}}{720}+\ldots .}\right)_{26}^{6}+\infty<x<\infty\\
\begin{array}{ll}
e^{\tan x}=1+x+\frac{x^{2}}{2}+\frac{x^{3}}{2}+\frac{3 x^{4}}{8}+\cdots & |x|<\frac{\pi}{2} \\
e^{x} \sin x=x+x^{2}+\frac{x^{3}}{3}-\frac{x^{5}}{30}-\frac{x^{6}}{90}+\frac{(\sqrt{2})^{2} \sin \left(\frac{m \pi}{4}\right) x^{n}}{n}+\cdots & -\infty<x<\infty
\end{array}\\
e^{x} \sin x=x+x^{2}+\frac{x^{3}}{3}-\frac{x^{5}}{30}-\frac{x^{6}}{90}+\cdots+\frac{(\sqrt{2})^{n} \sin \left(\frac{n \pi}{4}\right) x^{n}}{n !}+\cdots \quad-\infty<x<\infty
\end{array}
\]
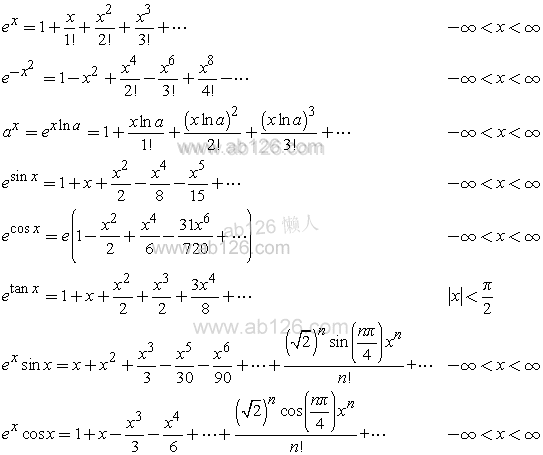


 浙公网安备 33010602011771号
浙公网安备 33010602011771号