第五章 解析函数的洛朗展式与孤立奇点

在前一章我们已经看出，用泰勒级数来表示圆形区域内的解析函数是很方便的.但是对于有些特殊函数，如贝塞尔（Bessel）函数，以圆心为奇点，就不能在奇点邻域内表成泰勒级数.为此，本章将建立（挖去奇点a的）圆环r<|z-a|<R（r≥0，R≤+0，，当r=0时为去心圆0<|z-a|<R）内解析函数的级数表示，并以它为工具去研究解析函数在孤立奇点邻域内的性质.

1.解析函数的洛朗展式

1.双边幂级数

考虑两个级数

\[\begin{array}{c} c_{0}+c_{1}(z-a)+c_{2}(z-a)^{2}+\cdots \\ \frac{c_{-1}}{z-a}+\frac{c_{-2}}{(z-a)^{2}}+\cdots \end{array}\]

前者是幂级数，故它在收敛圆|z-a|<R（0<R≤+o）内表一解析函数 f（z）.对第二个级数作代换
\(\zeta=\frac{1}{z-a}\)
则它成为一个幂级数

\[c_{-1} \zeta+c_{-2} \zeta^{2}+\cdots \cdot \cdot \]

设它的收敛区域为\(|ξ|<\frac{1}{r}\left(0<\frac{1}{r} \leqslant+\infty\right)\). 换回到原来的变数z，即知（5.2）在\(|z-a|>r（0≤r< + \infty）\)内表一解析函数f（z）.
当且仅当r<R时，（5.1）及（5.2）有公共的收敛区域即圆环H∶r<|z-a|<R.这时，我们称级数（5.1）与（5.2）之和为双边幂级数.可以表为

\[\sum_{n=-\infty}^{\infty} c_{n}(z-a)^{n}\tag{5.3} \]

由以上讨论及定理4.10和定理4.13得

定理5.1

设双边幂级数（5.3）的收敛圆环为\(H: r<|z-a|<R(r \geqslant 0, R \leqslant+\infty)\)
则（1）（5.3）在 H内绝对收敛且内闭一致收敛于

\[f(z)=f_1(z)+f_2(z) \]

（2）函数f（z）在 H内解析.
（3）函数 \(f（x）=\sum_{n=-\infty}^{\infty} c_{n}(z-a)^{n}\)
在H内可逐项求导p次（p=1，2，3...)
（4）函数 f（z）可沿 H内曲线C逐项积分. 注 定理5.1对应于定理4.13.

2.解析函数的洛朗展式

前面指出了双边幂级数在其收敛圆环内表一解析函数，反过来有

定理5.2（洛朗定理）

在圆环\(H∶r<|z-a|<R（r≥0，R ≤＋\infty)\)内解析的函数 f（z）必可展成双边幂级数

\[f(z)=\sum_{n=-\infty}^{\infty} c_{n}(z-a)^{n}\tag{5.4} \]

其中

\[c_{n}=\frac{1}{2 \pi \mathrm{i}} \int_{\Gamma} \frac{f(\zeta)}{(\zeta-a)^{n+1}} \mathrm{~d} \zeta \quad(n=0, \pm 1, \cdots)\tag{5.5} \]

\(\Gamma \text { 为圆周 }|\zeta-a|=\rho(r<\rho<R)\),并且展式是惟一的（即f（z）及圆环 H惟一地决定了系数\(c_n\)）.

定义5.1

（5.4）称为函数 f（z）在点 a的洛朗展式，（5.5）称为其洛朗系数，而（5.4）等号右边的级数则称为洛朗级数.

证明了洛朗展式的惟一性后，我们就可以采用一些常用的更简便的方法去求一些初等函数在指定圆环内的洛朗展开式（如例5.1至例5.5），只有在个别的情况下，才直接采用公式（5.5）求洛朗系数的方法（如例5.6）.

3.洛朗级数与泰勒级数的关系

当已给函数f(z)在点a处解析时，中心在 a，半径等于由 a到函数f（z）的最近奇点的距离的那个圆可以看成圆环的特殊情形，在其中就可作出洛朗级数展开式.根据柯西积分定理，由公式（5.5）可以看出，这个展式的所有系数\(c_n（n=1，2，，…）\)都等于零.在此情形下，计算洛朗级数的系数公式与泰勒级数的系数公式（积分形式）无异，所以洛朗级数就转化为泰勒级数.因此，泰勒级数是洛朗级数的特殊情形.

4.解析函数在孤立奇点邻域内的洛朗展

定义5.2

如果函数 f（z）在点 a的某一去心邻域\(K-\{a\}:0<|z-a|<R\)（即除去圆心a的某圆）内解析，点a是f（z）的奇点（见定义2.3），则称 a为f（z）的一个孤立奇点.

注 因函数f(z)在\(K-\{a\}\)内是单值的，故也称 a 为 f（z）的单值性孤立奇点;如以后遇到 f（z）在\(K-\{a\}\)内是多值的，则称a 为f（z）的多值性孤立奇点，即支点（由于在支点的邻域内函数能由一支变到另一支，故函数在支点邻域内缺少单值性.因而它以最简单的方式破坏了函数的解析性.因此支点也是函数的奇点）.以后如无特别声明，提到孤立奇点总指单值性孤立奇点.当然，以后也会遇到非孤立奇点.
如果 a为函数f（z）的一个孤立奇点，则必存在正数 R，使得f（z）在点 a的去心邻域\(K-\{a\}:0<|z-a|<R\)内可展成洛朗级数.

§2.解析函数的孤立奇点

孤立奇点是解析函数的奇点中最简单最重要的一种类型.以解析函数的洛朗展式为工具，我们能够在孤立奇点的去心邻域内充分研究一个解析函数的性质.

1.孤立奇点的三种类型

已经说过，如 a 为函数 f（z）的孤立奇点，则 f（x）在 a点的某去心邻域K-{a}内可以展成洛朗级数

\[f(z)=\sum_{n=-\infty}^{\infty} c_{n}(z-a)^{n} \]

我们称非负幂部分\(\sum_{n=0}^{\infty} c_{n}(z-a)^{n}\)为f（z）在点 a 的正则部分。而称负幂部分\(\sum_{n=1}^{\infty}c_{-n}(z-a)^{-n}\)为f(z)在点a的主要部分。这是因为实际上非负幂部分表示在点a的邻域K:|z-a|<R的解析函数，故函数f(z)在点a的奇异性质完全体现在洛朗级数的负幂部分上。

定义5.3

设 a为函数f（z）的孤立奇点.
（1）如果 f（z）在点 a的主要部分为零，则称a为f（z）的可去奇点（见例5.3）.
（2）如果 f（z）在点 a的主要部分为有限多项，设为

\[\frac{c_{-m}}{(z-a)^{m}}+\frac{c_{-(m-1)}}{(z-a)^{m-1}}+\cdots+\frac{c_{-1}}{z-a}\left(c_{-m} \neq 0\right) \]

则称a为f（z）的 m 阶极点（见例5.2）.一阶极点也称为单极点.
（3）如果 f（z）在点 a的主要部分有无限多项，则称 a为f（z）的本质奇点（见例5.4及例5.5）.
以下我们分别讨论三类孤立奇点的特征.

2.可去奇点

如果 a为函数 f（z）的可去奇点，则有

\[f(z)=c_{0}+c_{1}(z-a)+c_{2}(z-a)^{2}+\cdots(0<|z-a|<R) \]

上式等号右边表圆K∶|z-a|<R 内的解析函数.如果命\(f（a）=c_0\)，则f（z）在圆 K 内与一个解析函数重合.也就是说，我们将f（z）在点a 的值加以适当定义，则点 a就是f（z）的解析点.这就是我们称 a为f（z）的可去奇点的由来.
例如，当我们约定\(\frac {sinz} z|_{z=0}=1\)时，\(\frac {sinz} z\)就在z=0解析了。

定理5.3

如果 a为函数f（z）的孤立奇点，则下列三条是等价的.因此，它们中的任何一条都是可去奇点的特征.
（1）f（z）在点 a的主要部分为零;
(2)\(\lim_{z→a} f(z)=b(≠\infty);\)
（3）f（z）在点a的某去心邻域内有界.

3.施瓦茨（Schwarz）引理

如果函数 f（z）在单位圆|z|<1 之内解析，并且满足条件

\[f(0)=0,If(z)|<1(|z|<1) \]

, 则在单位圆|z|<1内恒有
\(|f(z)|≤|z|\), 且有\(|f(0)'|≤1\).
如果上式等号成立，或在圆|z|<1内一点 \(z_0≠0\)处前一式符号成立，则（当且仅当）

\[f(z)=e^{i\alpha}z,(|z|<1), \]

其中\(\alpha\)为一实常数.
从几何上看，施瓦茨引理表明∶任一解析变换 \(\omega=f（z）\)，f（0）=0，当它把单位圆变到一个单位圆内的区域 \(△\)上去时，圆内任一点z≠0的像都比 z 本身距坐标原点为近.而如果有一个点的像与这个点本身距坐标原点有相同距离的话，则\(△\)就与单位圆相同，变换就仅仅是一个旋转（图5.3）.

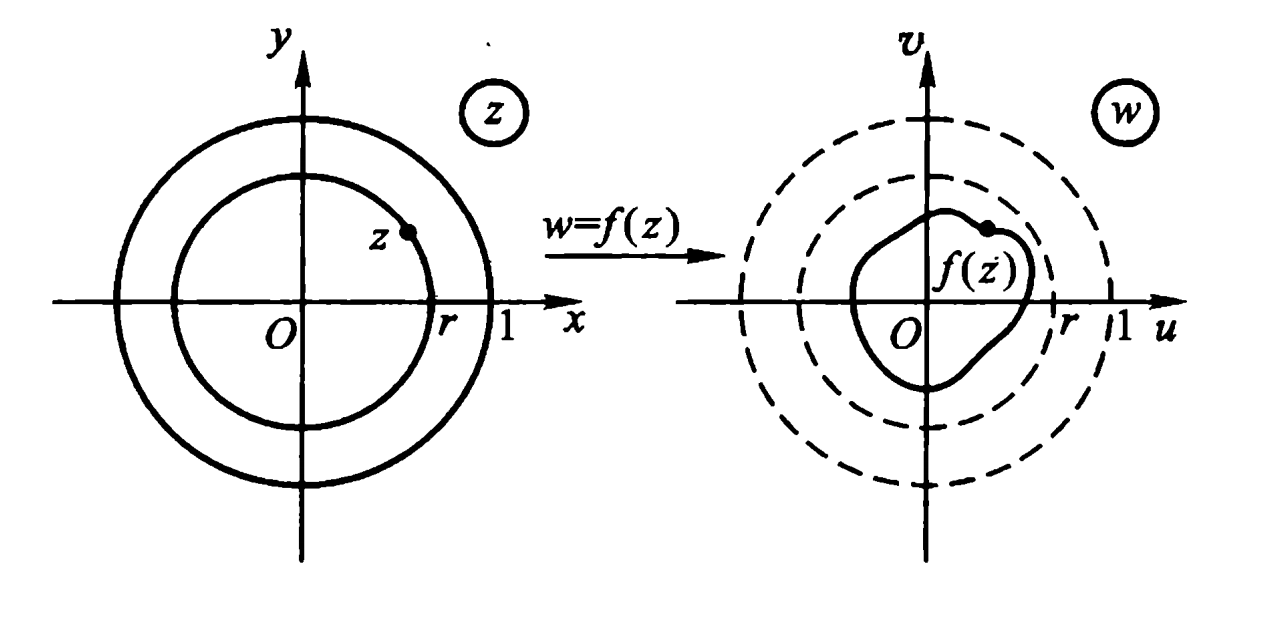
注 施瓦茨引理有如下一个简单改进;
我们保留假设条件不变.如果原点是函数 f（z）的 λ阶零点，就可以考虑函数∶\(\frac{f(z)}{z^\lambda}\),与刚才的情形一样，我们由此可以得到

\[|f(z)|\le|z|^{\lambda} \]

并且只有当\(f(z)=\mathrm{e}^{\mathrm{i} \alpha} z^{\lambda}\)（a为实数）时，等号才成立。这样，在这个特殊情形之下，函数的模就有了一个比前面公式中更小的界限.

4.极点

定理5.4

如果函数 f（z）以点 a为孤立奇点，则下列三条是等价的.因此，它们中的任何一条都是 m阶极点的特征.
（1）f（z）在点 a的主要部分为

\[\frac{c_{-m}}{(z-a)^{m}}+\cdots+\frac{c_{-1}}{z-a}\left(c_{-m} \neq 0\right) \]

（2）f（z）在点 a的某去心邻域内能表成

\[f(z)=\frac{\lambda(z)}{(z-a)^{m}}\tag{5.11} \]

其中λ（z）在点a邻域内解析，且λ（a）≠0;
(3)\(g(z)=\frac 1 {f(z)}\)以点 a为m 阶零点（可去奇点要当作解析点看，只要令g（a）=0）.
注 第（3）条表明∶
f(z)以点a为m阶极点\(\Leftrightarrow\)\(\frac 1 {f（z）}\)以点a为m 阶零点

定理5.5

函数 f（z）的孤立奇点 a为极点的充要条件是

\[lim_{z\rightarrow a}f(z)=\infty \]

5.本质奇点

定理5.6 函数 f（z）的孤立奇点 a为本质奇点的充要条件是

\[\lim _{z \rightarrow a} f(z) \neq\left\{\begin{array}{l} b(\text { 有限数 }) \\ \infty \end{array}\right.\]

即\(\lim f_{z\rightarrow a}（z）\)不存在.
这可由定理5.3.之（2）及定理5.5得到证明.

定理5.7

若z=a为函数f（z）之一本质奇点，且在点 a的充分小去心邻域内不为零，则z=a 亦必为
\(\frac 1 {f(z)}\)的本质奇点.