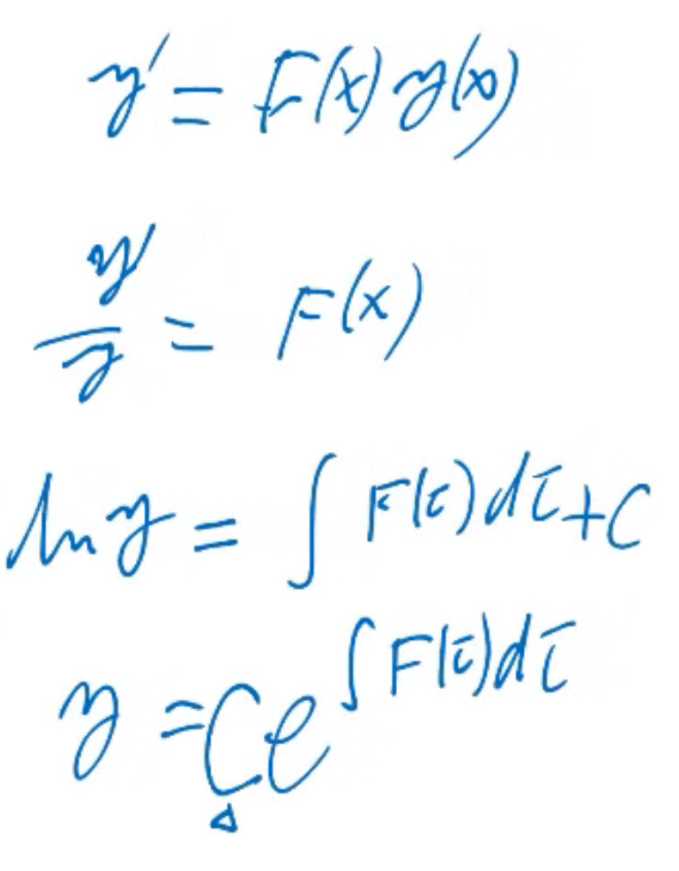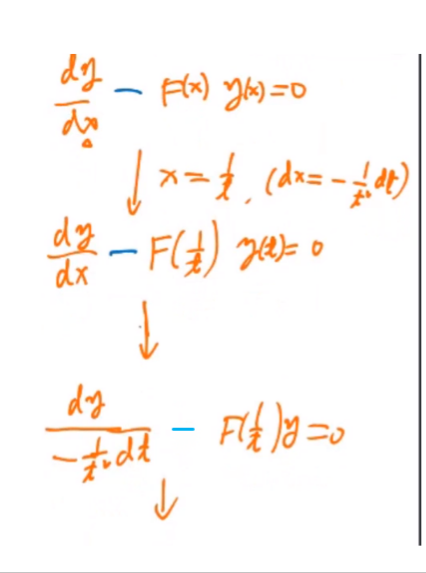4.1微分方程的奇点（李家春）

复习奇点

函数奇异点与方程奇异点不同

函数奇点分类

	极限角度	级数角度
解析点 &可去奇点 例\(\frac{\sin(x)}{x}\)	\(\lim_{x \to x_0} f(x)=A\) 级限存在且有限	无负幂项 \(\sum_{n=0}^{\infty}f_n\cdot(x-x_0)^n\)
极点 \(\frac {1}{{(x-x_0)}^2}\)	\(\lim_{x \to x_0} f(x)=\infty\)	有限个负幂项 \(\sum_{n=-m}^{\infty}f_n\cdot(x-x_0)^n\)
m阶极点	\(\lim_{x \to x_0} f(x)(x-x_0)^m=A\) \(\lim_{x \to x_0} f(x)(x-x_0)^{m-1}=\infty\)	最小次幂为-m \((x-x_0)^{-m}\sum_{k=0}^{\infty}f_k（x-x_0)^k\) \(\sum_{k=0}^{\infty}f_k（x-x_0)^k\)是解析的why
本性奇点	\(x\rightarrow x_0\),极限不存在 \(e^{\frac 1 z},z\rightarrow0^+\)是无穷大；\(z\rightarrow0^+\)是0	无穷个负项 \(\sum_{-\infty}^{+\infty}f_n(x-x_0)^n\)

枝点:
\(w=\sqrt{z-a}\)

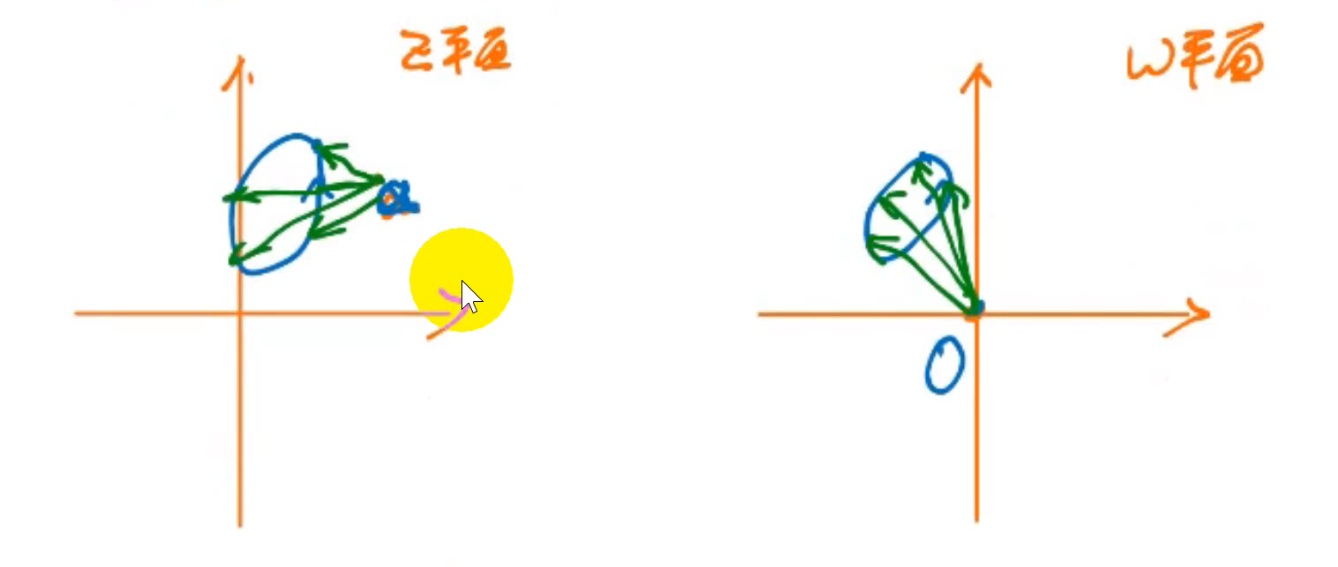
z平面内走一圈，\(\omega\)平面内也走一圈


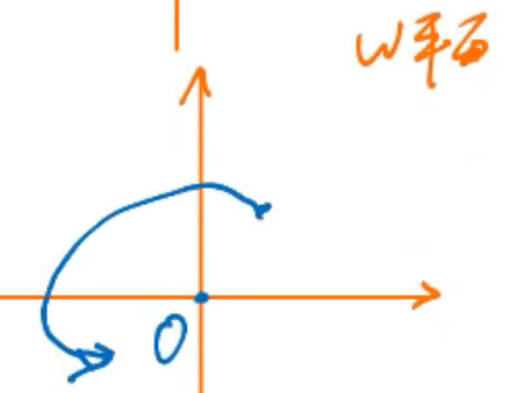
z平面内绕着a走一圈，\(\omega\)平面只走半圈
因为

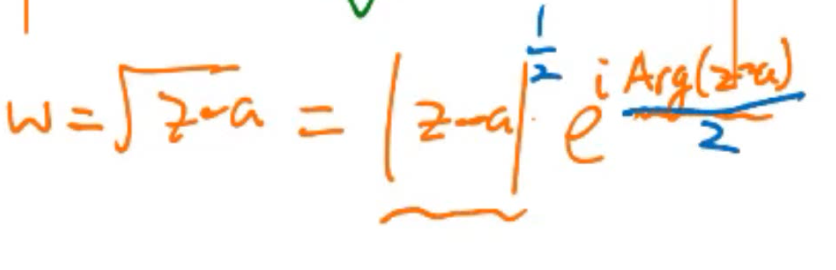
a是枝点

一般地说，对于多值函数w=f（z），若在绕某点一周，函数值w不复原，而在该点各单值分支函数值相同，则该为多值函数的支点。若当z绕支点n周，函数值w复原，便称该点为多值函数的n-1阶支点。

微分方程的奇点

讨论一阶常微分方程

\[y'(x) = F(x)y(x)\tag{4.1.1} \]

有通解\(y = Ce^{\int F(\tau)d\tau}\)

所以方程的解的性质被\(F(\tau)\)决定
若\(F(x)\)在\(x_0\)的邻域\(|x-x_0|<R\)内解析，则有泰勒展开

\[F(x) = \sum\limits_{n=0}^\infty F_n(x-x_0)^n \]

则，解可以写作

\[y = C\exp \left(\sum_{n=0}^\infty \frac{F_n(x-x_0)^{n+1}}{n+1}\right) \]

逐项积分得到

它亦是 \(x_0\)的邻域\(x_0\)的邻域\(|x-x_0|<R\)内的解析函数，这时，我们称 \(x_0\)为微分方程（4.1.1）的正常点（ordinary point）.
若 \(x_0\)为函数 F（x）的一阶极点，即 F（x）在 \(x_0\)点附近可表达为∶

\[F(x)=\frac{1}{x-x_{0}} \sum_{n=0}^{\infty} F_{n}\left(x-x_{0}\right)^{n} \]

F(x)展开为洛朗级数

\[\sum_{n=-1}^{\infty}\frac {c_n}{(x-x_0)^n} \]

乘以

\[\frac{x-x_0}{x-x_0} \]

求和号里-1项就没了

这时，方程的解为

\[y=c\left(x-x_{0}\right)^{F_{0}} \exp \left[F_{1}\left(x-x_{0}\right)+\frac{F_{2}}{2}\left(x-x_{0}\right)^{2}+\cdots\right] \]

\[\begin{align} y&=Ce^{\int F(t)dt} \\&=Ce^{\int{\frac 1 {x-x_0}\sum_{n=0}^{\infty}\quad (x-x_0)^n}d(x-x_0)} \\&=Ce^{[\int \frac{F_0}{x-x_0}+F_1+F_2(x-x_0)^1+\dots] d(x-x_0)} \\&=Ce^{[F_0\ln (x-x_0)+F_1(x-x_0)+\frac 1 2 F_2(x-x_0)^2+\dots]} \\&=Ce^{F_0\ln (x-x_0)}e^{[F_1(x-x_0)+\frac 1 2 F_2(x-x_0)^2+\dots]} \\&=C(x-x_0)^{F_0}e^{[F_1(x-x_0)+\frac 1 2 F_2(x-x_0)^2+\dots]} \end{align}\]

除了\(F_0\)为正整数外，\(x_0\) 点是方程（4.1.1）解的极点或支点，这时，我们称\(X_0\)为微分方程（4.1.1）的正则奇点（regular singular point）. 请注意，在正则奇点邻域内依然可以有解析解，譬如 \(F_0\)为正整数的情形.

\(F_0\)为负整数，\(x_0\)是极点。\(F_0\)为分数，\(x_0\)是支点。

若 \(x_0\)为函数 F（x）的二阶或二阶以上极点，即 F（x）在 \(x_0\) 点附近可表达成

\[F(x)=\frac{1}{\left(x-x_{0}\right)^{N}} \sum_{n=0}^{\infty} F_{n}\left(x-x_{0}\right)^{n}, \quad N \geq 2 \]

故方程（4.1.1）的解为

\[\begin{aligned} F &=c\left(x-x_{0}\right)^{F_{N-1}} \exp \left[\frac{-F_{0}}{(N-1)\left(x-x_{0}\right)^{N-1}}-\frac{F_{1}}{(N-2)\left(x-x_{0}\right)^{N-2}}\right.\\ &\left.-\cdots-\frac{F_{N-2}}{\left(x-x_{0}\right)}\right] \cdot \exp \left[F_{N}\left(x-x_{0}\right)+\frac{F_{N+1}}{2}\left(x-x_{0}\right)^{2}+\cdots\right] \end{aligned}\]

\[\begin{align} y&=Ce^{\int F(t)dt} \\&=Ce^{\int{\frac{1}{\left(x-x_{0}\right)^{N}} \sum_{n=0}^{\infty} F_{n}\left(x-x_{0}\right)^{n}}d(x-x_0)} \\&=Ce^{\int[\frac{F_0}{{(x-x_0)}^{N}}+\frac {F_1}{{(x-x_0)}^{N-1}}+\frac{F_2}{{(x-x_0)}^{N-2}}+\dots+F_n+F_{n+1}\quad(x-x_0)+F_{n+2}(x-x_0)^2+\dots] d(x-x_0)} \\&=Ce^{[\frac{-F_0}{(N-1)(x-x_0)^{N-1}}\quad+ \frac{-F_1}{(N-2)(x-x_0)^{N-2}}+\dots+F_{N-1}\ln{(x-x_0)}+F_N(x-x_0)+\frac 1 2 F_{N+1}(x-x_0)^2+\dots]} \\&=Ce^{F_{N-1}\ln (x-x_0)}e^{[\frac{-F_0}{(N-1)(x-x_0)^{N-1}}\quad+ \frac{-F_1}{(N-2)(x-x_0)^{N-2}}+\dots+\frac{-F_{N-2}}{(x-x_0)}+F_N(x-x_0)+\frac 1 2 F_{N+1}(x-x_0)^2+\dots]} \\&=C(x-x_0)^{F_{N-1}}e^{[\frac{-F_0}{(N-1)(x-x_0)^{N-1}}\quad+ \frac{-F_1}{(N-2)(x-x_0)^{N-2}}+\dots\frac{-F_{N-2}}{(x-x_0)}+F_N(x-x_0)+\frac 1 2 F_{N+1}(x-x_0)^2+\dots]} \end{align}\]

显然，xo 是方程的解的本性奇点.这时，我们称 \(x_0\)为微分方程（4.1.1）的非正则奇点（irregular singular point）.

因为出现了\(e^{\frac 1{x-x_0}}\),\(\quad x_0\)是本性奇点。

归纳起来，我们可以从微分方程系数的性质，确定奇点分类，并推断解的性质。

---

我们再来讨论二阶常微分方程

\[y^{\prime\prime}+p(x) y^{\prime}+q(x) y=0\tag{4.1.9} \]

的奇点类型。
若方程（4.1.9）的系数p（x），q（x）在\(| x一x_0| <R\)内解析.我们称 \(x_0\)为方程（4.1.9）的正常点.它的解至少在该邻域内解析.
若方程（4.1.9）的系数p（x），q（x），满足 \(p（x）（x-x_0），q（x）（x-x_0）^2\)，在$ |x-x_0|<R$内解析，我们称 \(x_0\) 为方程（4.1.9）的正则奇点，那么在该邻域内它的两个线性无关解的形式为∶

\(p（x）（x-x_0）\)解析，说明\(p(x)\)最多是一阶极点。同理，\(q(x)\)最多是二阶极点。

\[y_{1}(x)=\left(x-x_{0}\right)^{\rho_{1}} \sum_{n=0}^{\infty} c_{n}\left(x-x_{0}\right)^{n} \tag{4.1.10} \]

\[y_{2}(x)=\left(x-x_{0}\right)^{\rho_{2}} \sum_{n=0}^{\infty} d_{n}\left(x-x_{0}\right)^{n} \tag{4.1.11} \]

或

\[y_{2}(x)=g y_{1}(x) \ln \left(x-x_{0}\right)+\left(x-x_{0}\right)^{\rho_{2}} \sum_{n=0}^{\infty} d_{n}\left(x-x_{0}\right)^{n} \]

我们称（4.1.10）为Frobenius 型级数解，称（4.1.10），（4.1.11）为正则解.请注意，当\(\rho _1,\rho_2\)为零或正整数时，正则解是解析函数，所以，正则解包括了解析解的情况，否则就是极点或支点;

\(y_1\)是F型级数，\(y_2\)可能是F型级数，也可能是两个F型级数相加。

若方程（4.1.9）的系数 p（x），g（x）中至少有一个不满足 \(p（x）（x-x_0），q（x）（x-x_0）^2\)在 \(x_0\)解析的条件，我们称该点为方程（4.1.9）的非正则奇点.在该点邻域内至少有一个解在 xo点有本性奇点.

---

同样地，上述的奇点分类法可以推广到 n 阶常微分方程的情况∶

\[y^{(n)}+p_{n-1}(x) y^{(n-1)}+p_{n-2} y^{(n-2)}+\cdots+p_{0}(x) y=0\tag{4.1.12} \]

若方程（4.1.12）的系数\(p_0，p_1，…，P_{n-1}\)在\(x_0\)的邻域\(|x-x_0|<R\)内解析，我们称\(x_0\)为该方程的正常点，它的解至少在该邻域内解析;
若方程（4.1.12）的系数 \(p_0，p_1，…，P_{n-1}\)在\(x_0\)的邻域\(|x-x_0|<R\)内满足
\(p_{0}(x)\left(x-x_{0}\right)^{n}, p_{1}(x)\left(x-x_{0}\right)^{n-1}, \cdots, p_{n-1}(x)\left(x-x_{0}\right)\)解析的条件，我们称\(x_0\)为方（4.1.12）的正则奇点.它在\(|x-x_0|<R\) 内有n 个线性无关的正则解。

\[y(x)=\left(x-x_{0}\right)^{\gamma} \sum_{i=0}^{n-1}\left[\ln \left(x-x_{0}\right)\right]^{i} A_i(x)\tag{4.1.13} \]

式中，\(A_i\)是该邻域内的解析函数，注意，（4.1.13）包括了（4.1.10）（4.1.11）的形式有支点、极点的情况在内，也包括了解析的情况.
若方程（4.1.12）的系数 \(p_1，P_2，，P_{n-1}\)在\(x_0\)的邻域\(|x-x_0|<R\)内，至少有一个不满足\(p_{0}(x)\left(x-x_{0}\right)^{n}, p_{1}(x)\left(x-x_{0}\right)^{n-1}, \cdots, p_{n-1}(x)\left(x-x_{0}\right)\)解析的条件，我们称 \(x_0\)为方程（4.1.12）的非正则奇点，它至少有一个解在点\(x_0\)有本性奇点.
从上面关于奇点分类的结论中，我们看到，奇点的类型主要由微分方程的系数在该点邻域内的性态唯一决定的，而不是由解的性态唯一决定的，但我们却有如下的逆定理（Fuchs，1866）.
若微分方程（4.1.12）的所有线性独立解在\(x_0\)的邻域 \(|x-x_0| <R\)内是正则解（4.1.13）.那么 \(x_0\)至多是该方程的正则奇点.

---

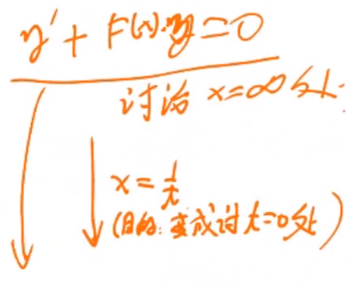
至于无穷远奇点的分类，这只要作变换

\[x=\frac 1 t\tag{4.1.14} \]

就可把无穷远点变换成原点，然后按通常的方法进行讨论，以一阶方程为例，在变换（4.1.14）下，原方程化成

\[\frac{d y}{d t}+F\left(\frac{1}{t}\right) \frac{1}{t^{2}} y=0 \tag{4.1.15} \]

\(\frac{d y}{d t}+F\left(\frac{1}{t}\right) \frac{1}{t^{2}} y=0\)

或

\[F(x)=\frac{1}{x^{n}} \sum_{i=0}^{\infty} \frac{a_{i}}{x^{i}}=t^{n} \sum_{i=0}^{\infty} a_{i} t^{i}\tag{4.1.16} \]

4.1.16带入4.1.15，得到 \(y'+\tilde{F}(t)y=0\)

因此

\[\tilde{F}(t)=F\left(\frac{1}{t}\right) \frac{1}{t^{2}}=t^{n-2} \sum_{i=0}^{\infty} a_{i} t^{i}\tag{4.1.17} \]

\[y'+\tilde {F}(t)y=0\tag{①} \]

若t是\(\tilde{F}\)的解析点，t是①的正常点.要求\(t^{n-2} \sum_{i=0}^{\infty} a_{i} t^{i}\)中的\(n\ge2\),也就要求\(F(x)=\frac{1}{x^{n}} \sum_{i=0}^{\infty} \frac{a_{i}}{x^{i}}\)的\(n\ge2\)
若t是\(\tilde{F}\)的一阶极点，t是①的正则奇点.

根据前面对一阶方程奇点分类的讨论，可得出如下结论∶
\(F(x) =\frac{1}{x^{2}}\left(a_{0}+\frac{a_{1}}{x}+\cdots\right)\)， \(\infty\)为正常点
\(F(x) =\frac{1}{x}\left(a_{0}+\frac{a_{1}}{x}+\cdots\right)\),\(\infty\)为正则奇点
\(F(x)\)为其他情况，\(\infty\)为非正则奇点

---

同样地, 我们可以讨论二阶常微分方程:

\[y^{\prime \prime}+p(x) y^{\prime}+q(x) y=0 \]

在 \(\infty\) 处的奇点分类, 结论如下: 若在 \(\infty\) 邻域内

\[\begin{aligned} &p(x)=\frac{2}{x}+\frac{p_{1}}{x^{2}}+\cdots \\ &q(x)=\frac{1}{x^{4}}\left(q_{0}+\frac{q_{1}}{x}+\cdots\right) \end{aligned} \]

那么, \(\infty\) 处为方程的正常点.
若在 \(\infty\) 邻域内

\[\begin{aligned} &p(x)=\frac{1}{x}\left(p_{0}+\frac{p_{1}}{x}+\cdots\right) \\ &q(x)=\frac{1}{x^{2}}\left(q_{0}+\frac{q_{1}}{x}+\cdots\right) \end{aligned} \]

那么, \(\infty\) 处为方程的正则奇点.
\(p(x), q(x)\) 在其它情况下, \(\infty\) 为方程的非正则奇点.
由于本章的重点是放在如何求微分方程的渐近解上, 对于奇点分类的一些证明, 我们不予蓛述, 有兴趣的读者可以参看有关书籍 (王竹溪 1965). 但我们还要举一些例子来说明上述这些定理的应 用, 因为正确地分析奇点类型是求解微分方程的前提.

---

[ 例 4.1.1] \(\quad(x-1)(2 x-1) y^{\prime \prime}+2 x y^{\prime}-2 y=0\).

\(y''+\frac{2y'}{(x-1)(2 x-1)}-\frac{2y}{(x-1)(2 x-1)}=0\)
\(p(x)=\frac{2}{(x-1)(2 x-1)},q(x)=\frac{2}{(x-1)(2 x-1)}\)

该方程在 \(x=1, x=\frac{1}{2}\) 是正则奇点(也是一阶极点), 它有两个解为 \(y_{1}=x, y_{2}=\frac{1}{x-1}\), 其中 \(y_{1}\)在该两奇点附近解析, \(y_{2}\) 的收㪉半径也超过系数的收佥半径.

[ 例 4.1.2] \(y^{\prime \prime}+\frac{1-x}{x} y^{\prime}-\frac{1}{x^{2}} y=0\)

x=0是p(x)的一阶极点，是q(x)的二阶极点

, 该方程在 \(x=0\) 有正则奇点, 它有两个解为 \(y_{1}=\frac{1+x}{x}, y_{2}=\frac{e^{x}-x-1}{x}\), 其中 \(y_{1}\) 在 \(x=0\) 有极点, \(y_{2}\) 在 \(x=0\) 解析.

[ 例 4.1.3] \(x^{\prime \prime}-\frac{1+x}{x} y^{\prime}+\frac{1}{x} y=0\)

x=0是p(x)的一阶极点，是q(x)的一阶极点

, 该方程在 \(x=0\) 有正则奇点, 但它的两个解 \(y_{1}=e^{x}, y_{2}=1+x\) 在那里均为解析函数.

[ 例 4.1.4] \(x^{3} y^{\prime \prime}+x(1-2 x) y^{\prime}-2 y=0\)

\(y^{\prime \prime}+\frac{(1-2 x)}{x^2} y^{\prime}-\frac 2{x^3} y=0\)
x=0是p(x)的二阶极点，是q(x)的三阶极点

, 该方程在 \(x=0\) 附 近有非正则奇点, 其解 \(y_{1}=x^{2}(1+2 x), y_{2}=x^{2} e^{\frac{1}{x}}(1-2 x)\), 其中 \(y_{2}\) 在 \(x=0\) 附近有本性奇点, 但 \(y_{1}\) 却是解析的.

[ 例 4.1.5] \(y^{\prime}=x^{\frac{1}{2}} y\)

x=0是支点，既不是正则奇点，也不是非正则奇点

, 它的解为

\[y=a e^{\frac{2}{3} x^{\frac{3}{2}}}=a \sum_{n=0}^{\infty} \frac{1}{n !}\left(\frac{2}{3} x^{\frac{3}{2}}\right)^{n} \]

注意, 该幂级数不是以整数次幂递增的, 所以它不是 Frobenius 型 的级数.

[ 例 4.1.6] \(y^{\prime \prime}+(1+3 x) y^{\prime}+y=0\)

, 我们可形式地求幂级 数解

\[y=\sum_{n=0}^{\infty}(-1)^{n} n ! x^{n} \]

虽然它是以整数次幂递增的, 但它也不是 Frobenius 型的级数, 因 为它是发散的.

F型级数收敛

上面这些例子, 都给我们指出了, 应用奇点分类定理时, 千万 不要单纯地从解的形式来判断奇点的类型.

[ 例 4.1.7] Bessel 函数满足方程

\[x^{2} y^{\prime \prime}+x y^{\prime}+\left(x^{2}-\nu^{2}\right) y=0 \]

\(y^{\prime \prime}+\frac 1 x y^{\prime}+\frac {\left(x^{2}-\nu^{2}\right)}{x^2} y=0\)
x=0,是p(x)一阶极点，是q(x)二阶极点；
\(x=\infty\)，p(x)不符合\(p(x)=\frac{2}{x}+\frac{p_{1}}{x^{2}}+\cdots\)，符合\(p(x)=\frac{1}{x}\left(p_{0}+\frac{p_{1}}{x}+\cdots\right)\)。q(x)不符合\(q(x)=\frac{1}{x^{2}}\left(q_{0}+\frac{q_{1}}{x}+\cdots\right)\)。所以是非正则奇点。

从方程可知, Bessel 函数在 \(x=0\) 为正则奇点, \(x=x\) 为非正则奇点.

[ 例 4.1.8] 超越几何函数满足方程

\[x(1-x) y^{\prime \prime}+[c-(a+b+1) x] y^{\prime}-a b y=0 \]

\(y^{\prime \prime}+\frac{[c-(a+b+1) x]}{x(1-x)} y^{\prime}-\frac{a b }{x(1-x)}y=0\)
\(p(x)=\frac{[c-(a+b+1) x]}{x(1-x)},q(x)=-\frac{a b }{x(1-x)}\)

它在 \(x=0,1, \infty\) 处有奇点, 奇点的类型讨论如下:

• \(x=0, c \neq 0\) 为正则奇点, \(a b=0, c=0\) 为正常点.
• \(x=1\), 一般为正则奇点, \(a b=0, c=a+b+1\) 为正常点.
• \(x=\infty\), 一般是正则奇点; \(a b=0, a+b=1\) 为正常点.

\[x=\infty,t=\frac 1 x,\\ p(t)=p(x)=\frac{[c-(a+b+1) \frac 1 t]}{(\frac 1 t)(1-\frac 1 t)}\\ p(t)(t-0)=\frac{[c-(a+b+1) \frac 1 t]t}{(\frac 1 t)(1-\frac 1 t)}=\frac{[ct-(a+b+1) ]}{\frac {t-1}{t^2}}=t^2\frac{[ct-(a+b+1) ]}{t-1}\\ \lim_{t\rightarrow0}t^2\frac{[ct-(a+b+1) ]}{t-1}=0，是有限值\\ q(t)t^2=-\frac{a b t^2}{\frac 1 t(1-\frac 1 t)}\\ \lim_{t\rightarrow0}q(t)t=0,是有限值 所以是正则奇点 \]

https://img2020.cnblogs.com/blog/2573690/202111/2573690-20211114170921910-331156817.jpg
https://img2020.cnblogs.com/blog/2573690/202111/2573690-20211114171006885-403168453.jpg

\[\]