支持向量机

 

支持向量机最早是二分类算法，主要解决数学中线性可分和线性不可分以及非线性问题。

一、支持向量机原理

1、线性可分

H1、H2为两条分别穿过两类距离H最近的样本并且与最优分类线平行的直线。H1、H2穿过的两类样本称为支持向量。

将求解最优线性分类面转化为二次规划问题：

引入拉格朗日函数

2、线性不可分

与线性可分类似，只不过引入惩罚因子。

约束条件变为：

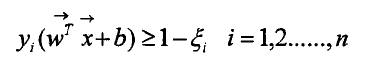
拉格朗日函数为：

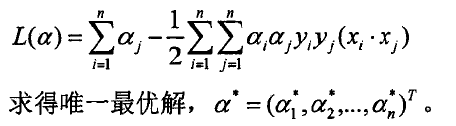
3、非线性可分

可利用非线

性变换将训练向量映射到更高维度空间中，这样就变得线性可分了。

定义核函数，常用的核函数有线性核函数、多项式核函数和径向基核函数。

三种不同核函数的具体定义如下：

二、支持向量机的结构

1、一对多分类

    在N类分类样本中建立N个二值分类器，第i个支持向量机分类器用第i个样本数据作为正面样本，其他数据为反面样本训练。把每类样本分别输送到N个二值分类器中，输出值最大的那个二值分类器，即为该样本所对应的种类。分类函数为：

2、一对一分类

    建立N(N-1)/2个分类器，分类函数为：

样本被输送至所有分类器进行决策判断，每一个样本分类器会对该样本进行投票，该样本属于得票数最多的样本。

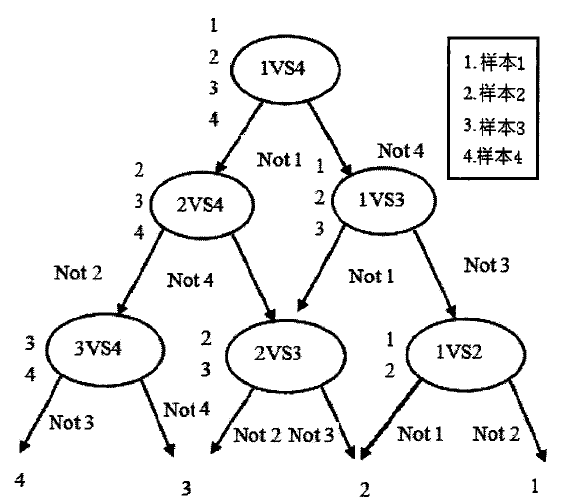
3、导向无环图支持向量机分类器

建立N(N-1)/2个分类器，类似于二叉树，顶层只有唯一结点。结构如下图所示。

4、二叉树支持向量机

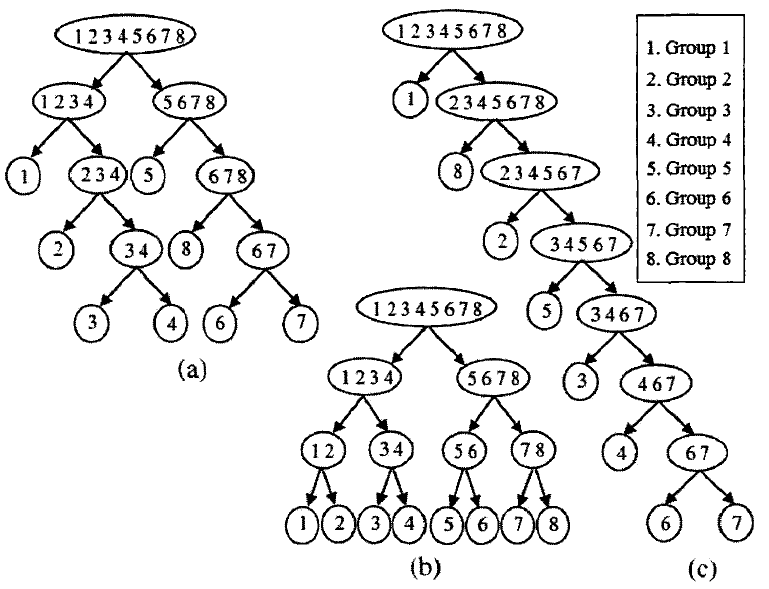
与顶层结构关系最大，因此最容易区分的样本应放置在最顶端进行分类。

支持向量机的识别效果在很大程度上取决于参数。但是参数并无公式可寻，很大程度依赖于经验。