LeetCode 84. 柱状图中最大的矩形(Largest Rectangle in Histogram)
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
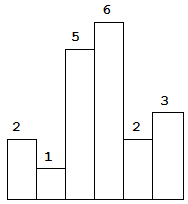
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
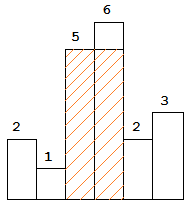
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
解题思路
这道题跟LeetCode 11很相似,但是因为考虑柱子宽度,因此解题技巧不相同,此题考查单调栈的应用。我们首先在数组最后加入0,这是为了方便处理完数组中的所有高度数据。假设存储高度坐标的栈为stack,当前处理的高度坐标为i(i∈[0→n]):
- 如果当前stack为空,或者heights[i]大于等于栈顶坐标对应高度,则将i加入stack中,并将i加一;
- 如果heights[i]小于栈顶坐标对应高度,说明可以开始处理栈内的坐标形成的局部递增高度,以求得当前最大矩形面积。弹出当前栈顶坐标 = top,此时栈顶新坐标 = top',那么对应计算面积的宽度w = i - 1 - top'(若弹出栈顶坐标后,stack为空,则对应w = i),得到面积s = heights[top] * w,再次返回2检查栈;
- 遍历完成i∈[0→n],返回最大矩形面积。
代码
1 class Solution { 2 public: 3 int largestRectangleArea(vector<int>& heights) { 4 stack<int> s; 5 int i = 0, maxArea = 0; 6 heights.push_back(0); 7 while(i < heights.size()){ 8 if(s.empty() || heights[s.top()] <= heights[i]){ 9 s.push(i); 10 i++; 11 } 12 else{ 13 int top = s.top(); 14 s.pop(); 15 int l = s.empty() ? i : i - s.top() - 1; 16 maxArea = max(maxArea, heights[top] * l); 17 } 18 } 19 return maxArea; 20 } 21 };
参考自




