梯度提升树GBDT总结

　　提升树的学习优化过程中，损失函数平方损失和指数损失时候，每一步优化相对简单，但对于一般损失函数优化的问题，Freidman提出了Gradient Boosting算法，其利用了损失函数的负梯度在当前模型的值：

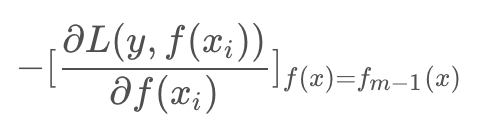
　　作为回归问题提升树算法的残差近似值，去拟合一个回归树。

 

函数空间的数值优化

　　优化目标是使得损失函数最小，(N是样本集合大小)：

　　GBDT是一个加法模型： f_m(x) 是每一次迭代学习的到树模型

　　对于其每一步迭代：

　　其中

 

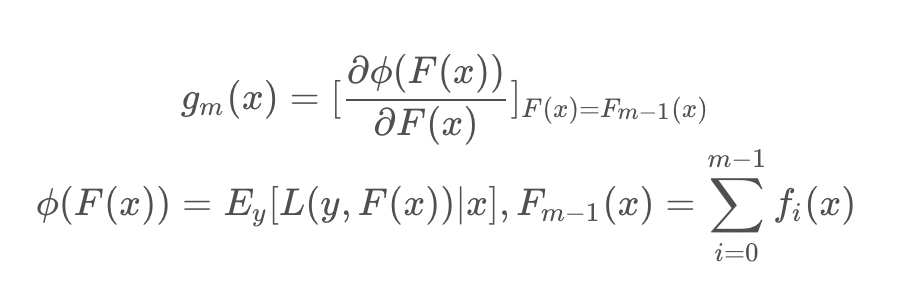
　　其实 L(y,F(x)) 就是损失函数，Φ(F(x)) 是当前x下的损失期望，g_m(x) 是当前x下的函数梯度。最终 f_m(x) 学习的是损失函数在函数空间上的负梯度。

　　对于权重 ρ_m 通过线性搜索求解：

　　理解：每一次迭代可以看做是采用梯度下降法对最优分类器 F^*(x) 的逐渐比较，每一次学习的模型 f_m(x) 是梯度，进过M步迭代之后，最后加出来的模型就是最优分类器的一个逼近模型，所以 f_m(x_i) 使用单步修正方向 -g_m(x_i)：

　　这里的梯度变量是函数，是在函数空间上求解（这也是后面XGBoost改进的点），注意以往算法梯度下降是在N维的参数空间的负梯度方向，变量是参数。这里的变量是函数，更新函数通过当前函数的负梯度方向来修正模型，使它更优，最后累加的模型近似最优函数。

 

算法描述

　　输入：训练数据集 T={(x₁,y₁),(x₂,y₂),···,(x_N,y_N)}

　　输出：回归树 f_M(x)

　　1. 初始化

　　2. 对 m=1,2,…M

　　　　a. 对 i=1,2,…,N ，计算

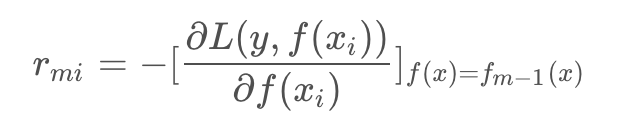
　　　　b. 对 r_mi 拟合一颗回归树，得到第m棵树的叶结点区域 R_mj, j=1,2,…,J ,即一棵由J个叶子节点组成的树

　　　　c. 对  j=1,2,…,J ,计算

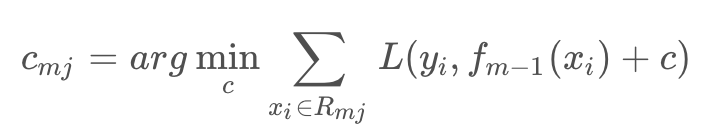
　　　　上面两步相当于回归树递归在遍历所有切分变量j和切分点s找到最优j,s，然后在每个节点区域求最优的c

　　　　d. 更新

　　3. 得到回归树

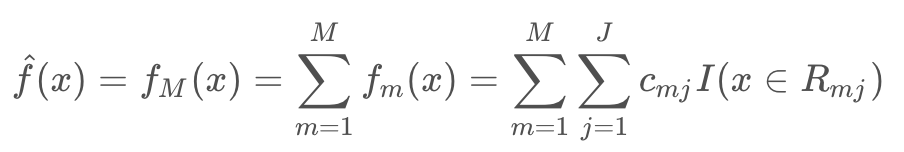
　　在回归树生成时，建树选择分裂点必须要遍历所有数据在每个特征的每个切分点的值，如果是连续特征就计算复杂度非常大，也是GBDT训练主要耗时所在。

 

参考

GBDT原理-Gradient Boosting Decision Tree