为什么ROC曲线不受样本不均衡问题的影响

转自：https://blog.csdn.net/songyunli1111/article/details/82285266 

在对分类模型的评价标准中，除了常用的错误率，精确率，召回率和F1度量外，还有两类曲线：ROC曲线和PR曲线，它们都是基于混淆矩阵，在不同分类阈值下两个重要量的关系曲线。

在二分类问题中，分类器将一个实例分类为正样本和负样本，全部分类样本可以用一个混淆矩阵来表示。混淆矩阵有四个分类，如下表:

 

对于PR曲线，它是精确率（precision，简称P）和召回率（Recall，简称R）的关系曲线，计算式如下：

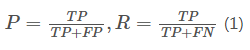
对于ROC曲线，它是“真正例率”(True Positive Rate, 简称TPR)，横轴是“假正例率”(False Positive Rate,简称FPR)的关系曲线，计算式如下：

真正例率是在所有正例中，你将多少预测为了正例，这是你希望最大化的，也可以看作收益；假正例率是在所有负例中，你又将多少预测为了正例，这是你希望最小化的，也可以看作代价。

从公式(2)和表中可以看出，TPR考虑的是第一行，实际都是正例，FPR考虑的是第二行，实际都是负例。因此，在正负样本数量不均衡的时候，比如负样本的数量增加到原来的10倍，那TPR不受影响，FPR的各项也是成比例的增加，并不会有太大的变化。因此，在样本不均衡的情况下，同样ROC曲线仍然能较好地评价分类器的性能，这是ROC的一个优良特性，也是为什么一般ROC曲线使用更多的原因。

而看公式(1)和表，精确率P考虑的是第一列，实际中包括正例和负例，因此，正负样本数量的变化会引起该值的变化，进而影响PR曲线对分类器的评价。

下图是ROC曲线和PR曲线的对比：

 

 

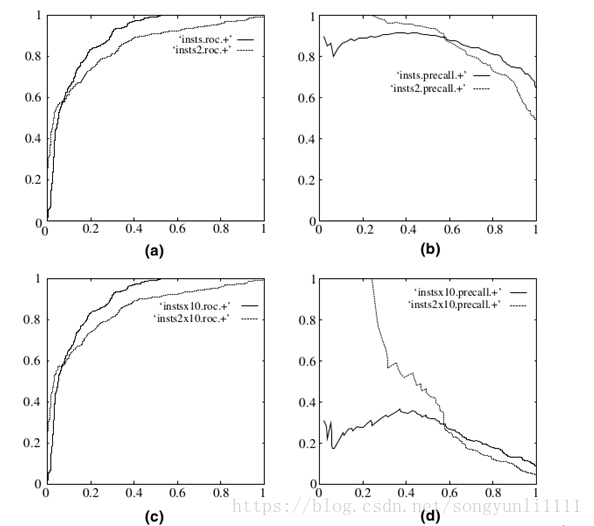
a,c为ROC曲线，b,d为PR曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果，(c)(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果，可以明显的看出，ROC曲线基本保持原貌，而PR曲线变化较大。