近似最近邻算法-annoy解析

转自https://www.cnblogs.com/futurehau/p/6524396.html

Annoy是高维空间求近似最近邻的一个开源库。

Annoy构建一棵二叉树，查询时间为O(logn)。

Annoy通过随机挑选两个点，并使用垂直于这个点的等距离超平面将集合划分为两部分。

如图所示，图中灰色线是连接两个点，超平面是加粗的黑线。按照这个方法在每个子集上迭代进行划分。

依此类推，直到每个集合最多剩余k个点，下图是一个k = 10 的情况。

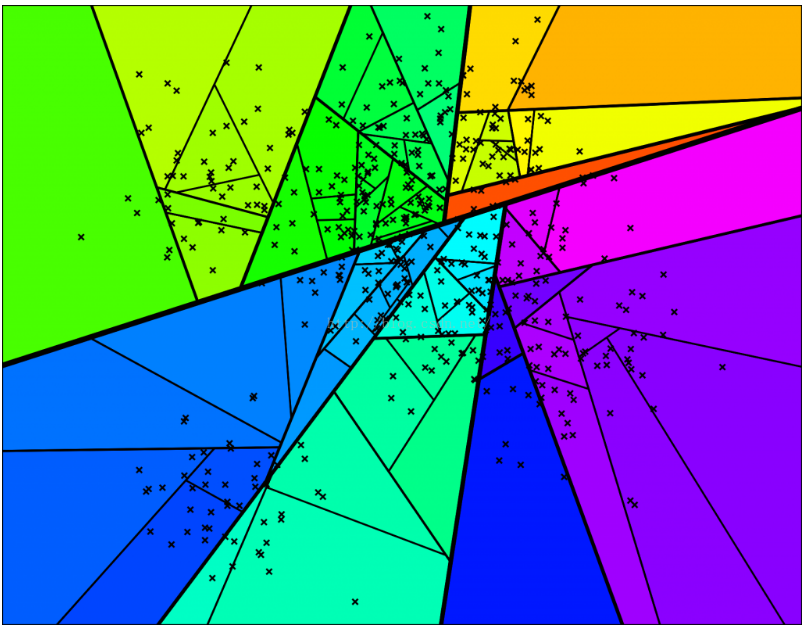
相应的完整二叉树结构：

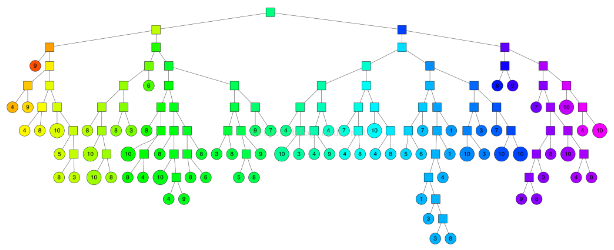
随机投影森林。

一个思想依据是：在原空间中相邻的点，在树结构上也表现出相互靠近的特点，也就是说，如果两个点在空间上相互靠近，那么他们很可能被树结构划分到一起。

如果要在空间中查找临近点，我们可以在这个二叉树中搜索。上图中每个节点用超平面来定义，所以我们可以计算出该节点往哪个方向遍历，搜索时间 log n

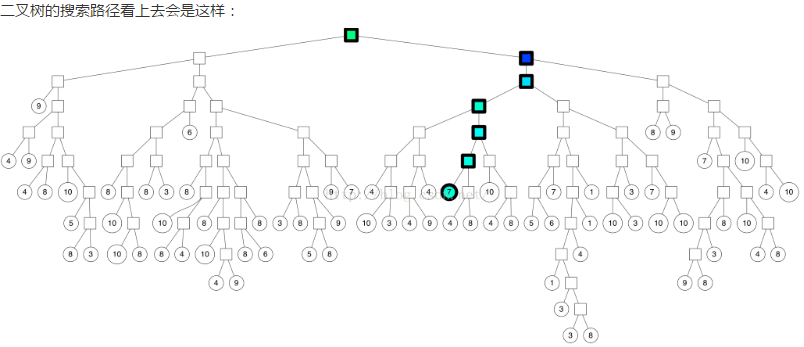
如上图，我们找到了七个最近邻，但是假如我们想找到更多的最近邻怎么办？有些最近邻是在我们遍历的叶子节点的外边的。

技巧1：使用优先队列

如果一个划分的两边“靠得足够近”（量化方式在后面介绍），我们就两边都遍历。这样就不只是遍历一个节点的一边，我们将遍历更多的点

我们可以设置一个阈值，用来表示是否愿意搜索划分“错”的一遍。如果设置为0，我们将总是遍历“对”的一片。但是如果设置成0.5，就按照上面的搜索路径。

这个技巧实际上是利用优先级队列，依据两边的最大距离。好处是我们能够设置比0大的阈值，逐渐增加搜索范围。

技巧2：构建一个森林

我们能够用一个优先级队列，同时搜索所有的树。这样有另外一个好处，搜索会聚焦到那些与已知点靠得最近的那些树——能够把距离最远的空间划分出去

每棵树都包含所有的点，所以当我们搜索多棵树的时候，将找到多棵树上的多个点。如果我们把所有的搜索结果的叶子节点都合在一起，那么得到的最近邻就非常符合要求。

 

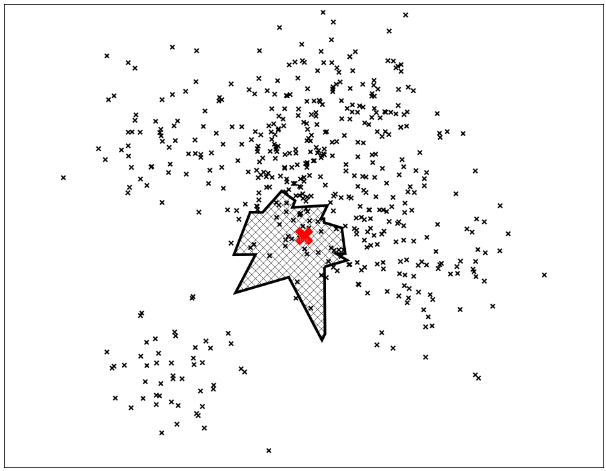
依照上述方法，我们找到一个近邻的集合，接下来就是计算所有的距离和对这些点进行排序，找到最近的k个点。

很明显，我们会丢掉一些最近的点，这也是为什么叫近似最近邻的原因。

Annoy在实际使用的时候，提供了一种机制可以调整（搜索k），你能够根据它来权衡性能（时间）和准确度（质量）。

tips:

1.距离计算，采用归一化的欧氏距离：vectors = sqrt(2-2*cos(u, v)) 

2.向量维度较小（<100）,即使维度到达1000变现也不错

3.内存占用小

4.索引创建与查找分离（特别是一旦树已经创建，就不能添加更多项）

5.有两个参数可以用来调节Annoy 树的数量n_trees和搜索期间检查的节点数量search_k

　　n_trees在构建时提供，并影响构建时间和索引大小。 较大的值将给出更准确的结果，但更大的索引。

　　search_k在运行时提供，并影响搜索性能。 较大的值将给出更准确的结果，但将需要更长的时间返回。

如果不提供search_k，它将默认为n * n_trees，其中n是近似最近邻的数目。 否则，search_k和n_tree大致是独立的，即如果search_k保持不变，n_tree的值不会影响搜索时间，反之亦然。 基本上，建议在可用负载量的情况下尽可能大地设置n_trees，并且考虑到查询的时间限制，建议将search_k设置为尽可能大。