20202315 实验九《数据结构与面向对象程序设计》实验报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 王梦欣
学号:20202315
实验教师:王志强
实验日期:2021年12月21日
必修/选修: 必修
## 1.实验内容
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
PS:本题12分。目前没有明确指明图的顶点和连通边,如果雷同或抄袭,本次实验0分。
实验报告中要根据所编写的代码解释图的相关算法
## 2.实验过程及结果
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
·这里我使用的是邻接矩阵实现无向图及有向图的初始化
码云链接:
在草稿纸上画出图,如下:
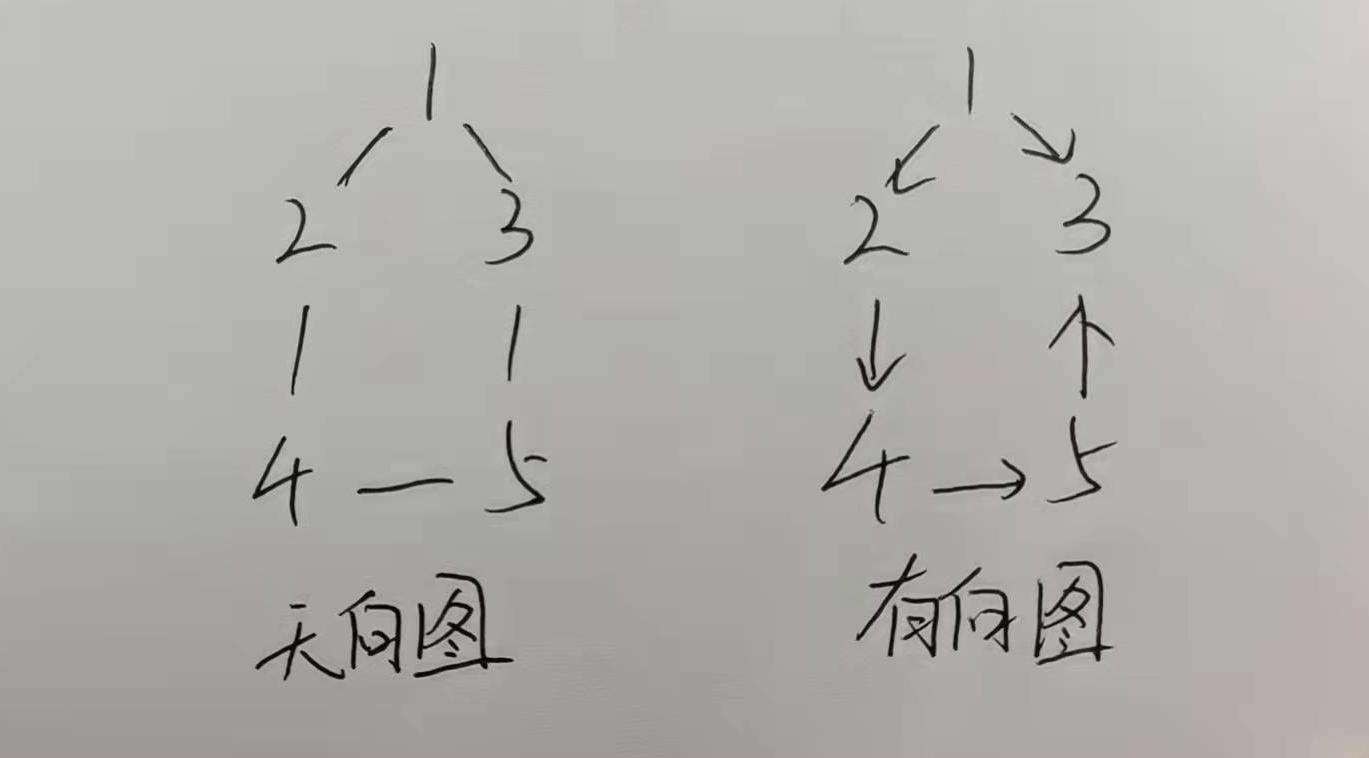
运行结果截图如下:
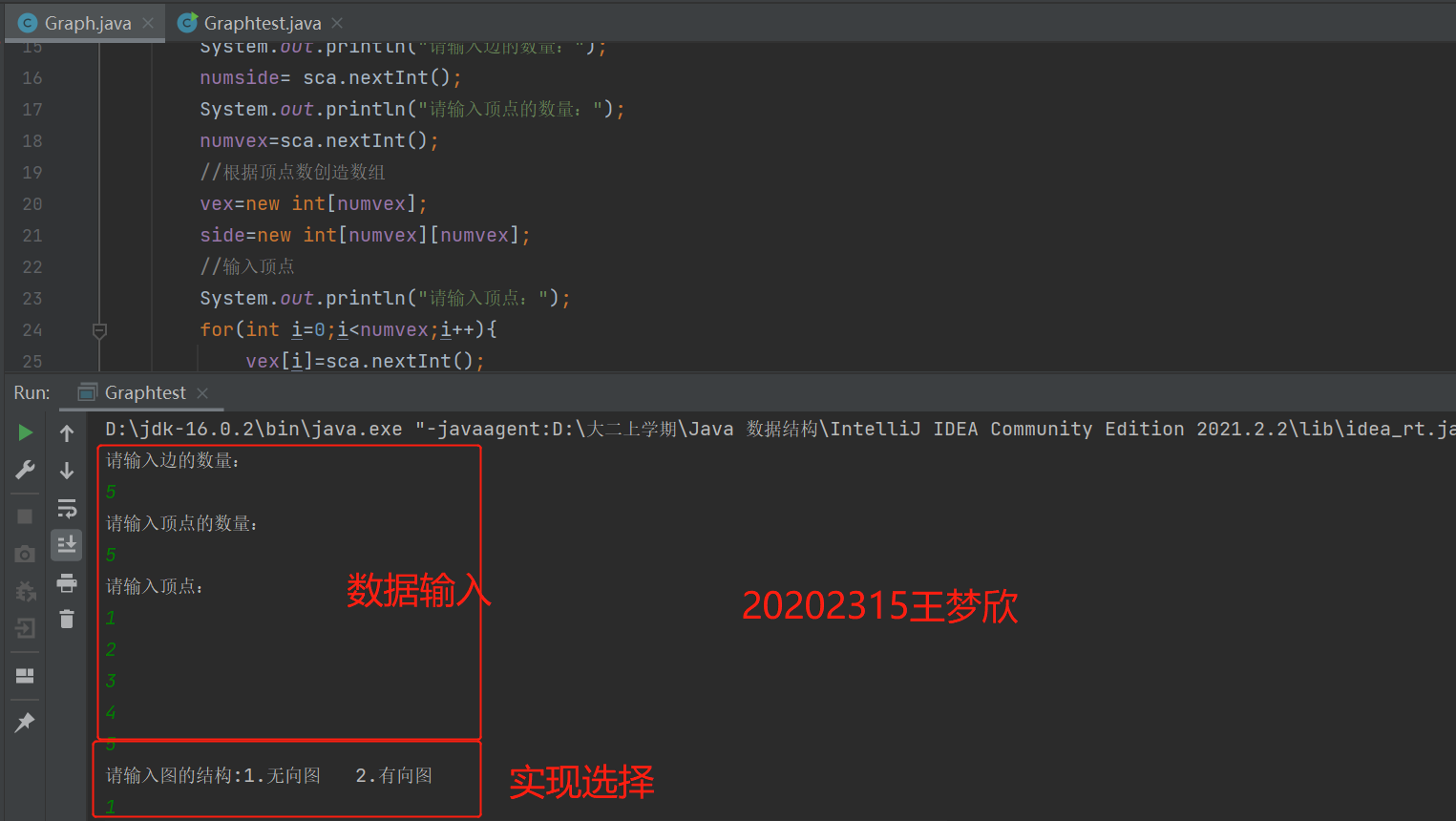
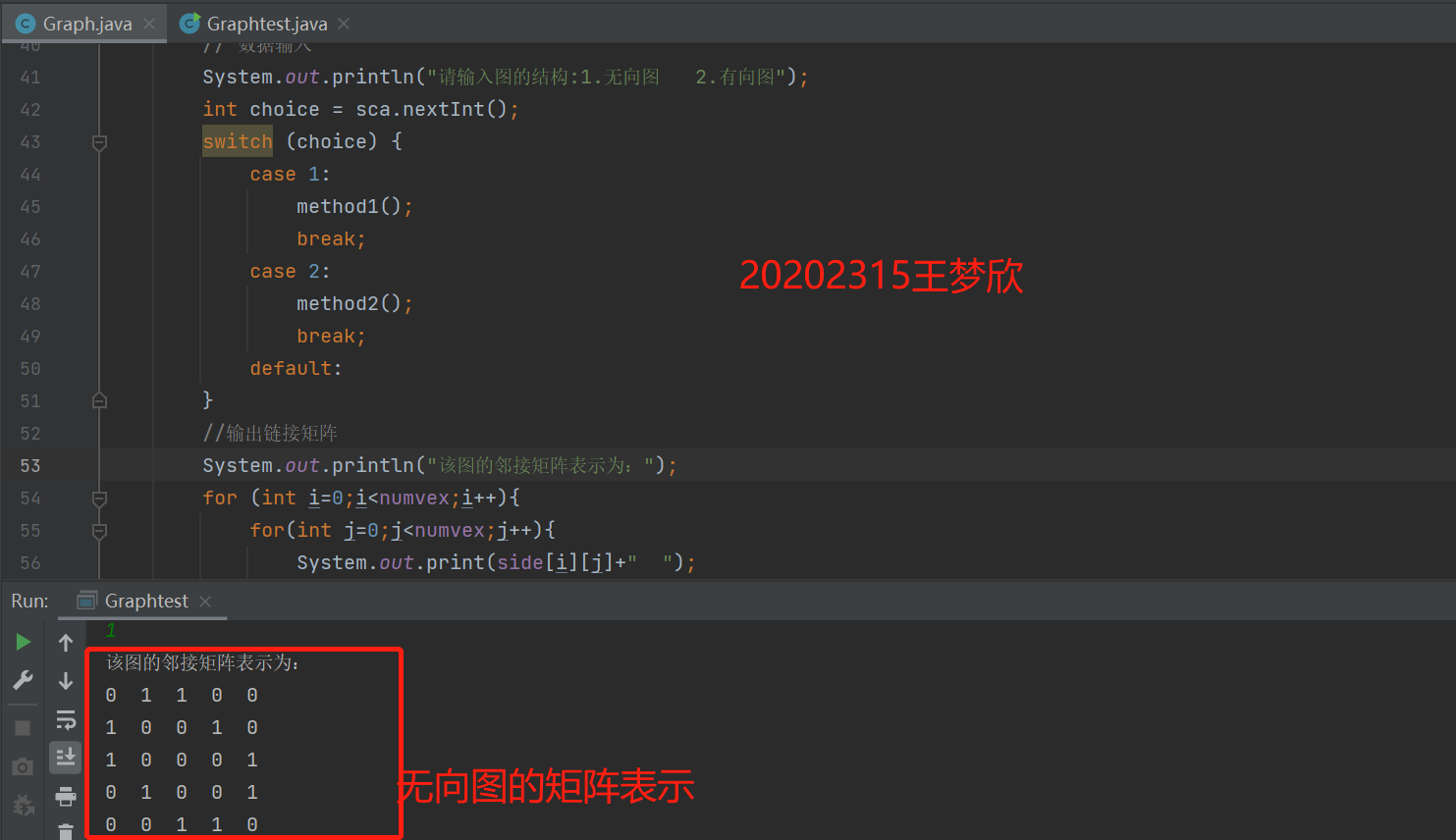

(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
主要代码:
//得到第一个邻接结点的下标 public int getFirstNeighbor(int index){ for (int j=0;j<numvex;j++){ if(side[index][j]>0){ return j; } } return -1; } //根据前一个邻接结点的下标来确定下一个邻接结点 public int getNextNeighbor(int v1,int v2){ for(int j=v2+1;j<numvex;j++){ if(side[v1][j]>0){ return j; } } return -1; } //私有函数,深度优先遍历 private void depthFirstSearch(boolean[] isVisited,int i){ //首先访问该结点,在控制台打印出来,置该结点为已访问 System.out.print(vex[i]+" "); isVisited[i]=true; int w=getFirstNeighbor(i); while(w!=-1){ if(!isVisited[w]){ depthFirstSearch(isVisited,w); } w=getNextNeighbor(i,w); } } //对外公开函数,深度优先遍历,与其同名私有函数属于方法重载 public void depthFirstSearch(){ boolean[] isVisited = new boolean[100]; for(int i=0;i<numvex;i++){ if(!isVisited[i]){ depthFirstSearch(isVisited,i); } } } //私有函数,广度优先遍历 private void broadFirstSearch(boolean[] isVisited,int i){ int u,w; LinkedList quene = new LinkedList(); //首先访问该结点,置该结点为已访问 System.out.print(vex[i]+" "); isVisited[i]=true; //结点进入队列 quene.addLast(i); while (!quene.isEmpty()){ u=((Integer)quene.removeFirst()).intValue(); w=getFirstNeighbor(u); while(w!=-1){ if(!isVisited[w]){ //访问该结点、标记并入队列 System.out.print(vex[w]+" "); isVisited[w]=true; quene.addLast(w); } //寻找下一个邻接结点 w=getNextNeighbor(u,w); } } } //对外公开函数,广度优先遍历 public void broadFirstSearch(){ boolean[] isVisited = new boolean[100]; for(int i=0;i<numvex;i++){ if(!isVisited[i]){ broadFirstSearch(isVisited,i); } } }
运行结果截图:
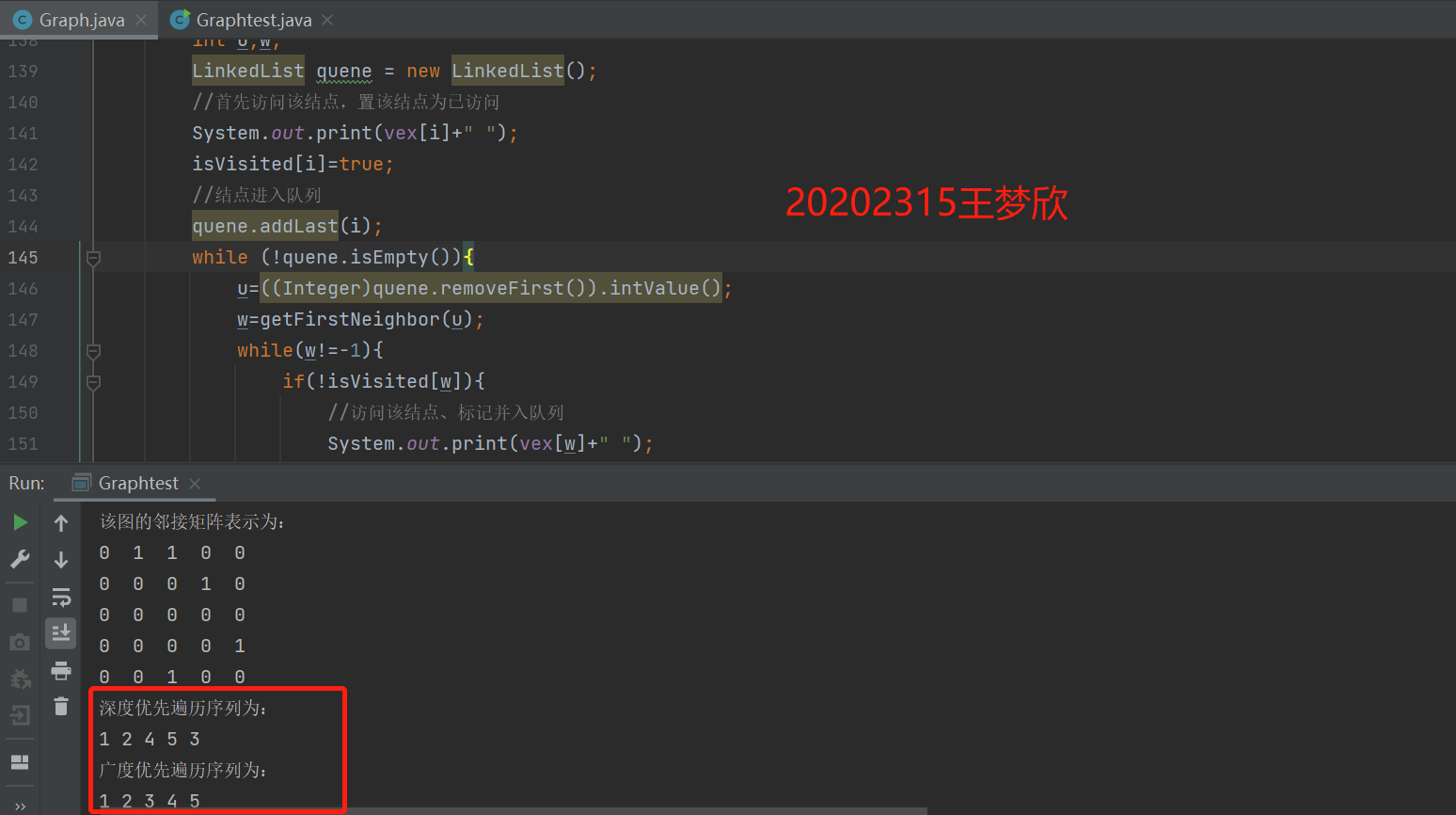
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环
实现该功能的过程十分曲折,多次调试之后才发现问题出在一个很小的点上,由于我每次输入结点都是1,2,3,4...,所以想当然的将其与数组的【1】【2】【3】...对应
调试之后才发现这一细节问题所在。
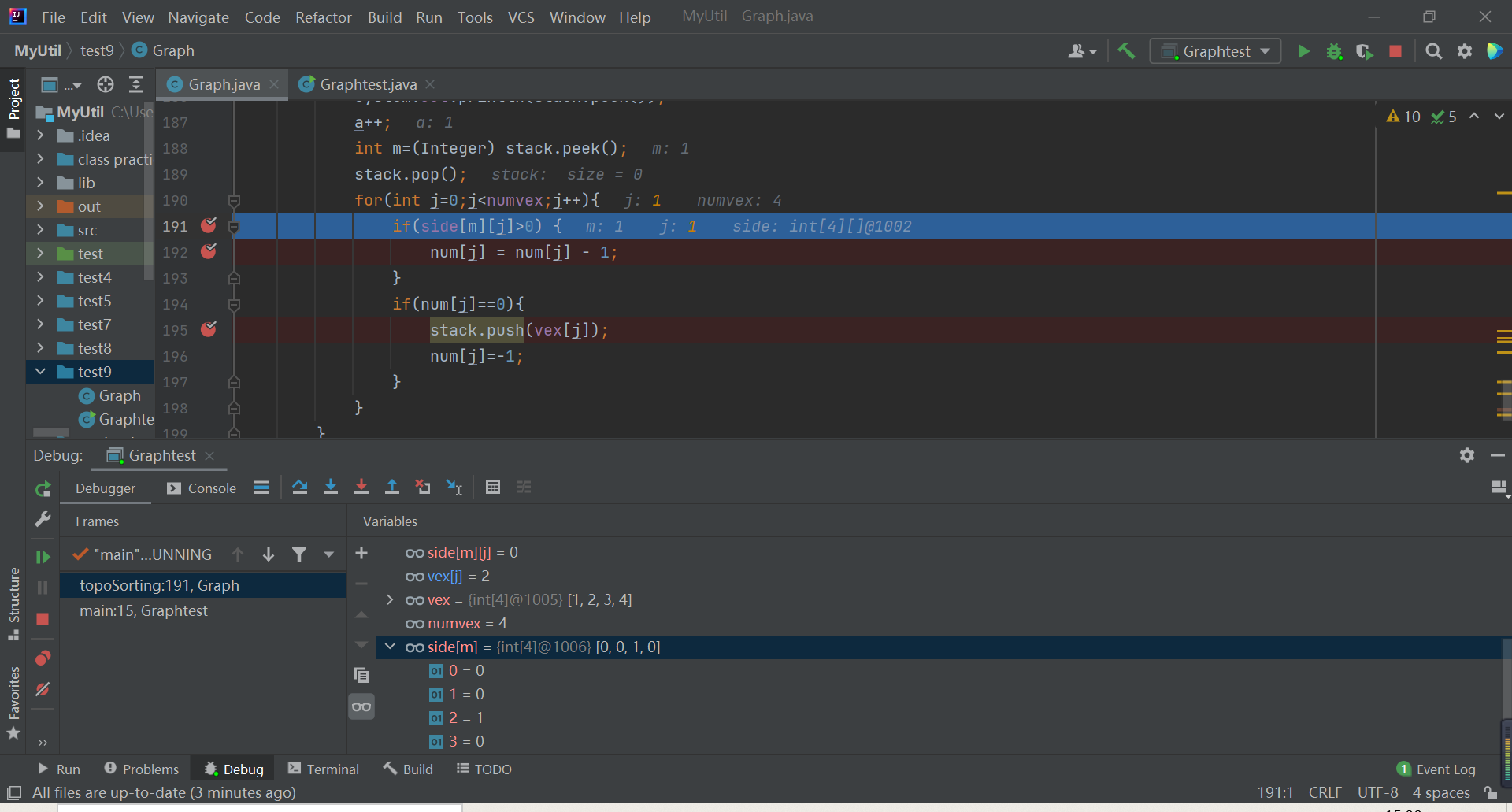
主要代码:
//拓扑排序 public void topoSorting(){ System.out.println("拓扑排序:"); int a=0; Stack stack = new Stack(); int[] num=new int[numvex]; for(int j=0;j<numvex;j++){ num[j] = 0; for(int i=0;i<numvex;i++){ num[j]=num[j]+side[i][j]; } if(num[j]==0){ stack.push(vex[j]); num[j]=-1; } } while (!stack.isEmpty()){ System.out.print(stack.peek()+" "); a++; int m=(Integer) stack.peek(); stack.pop(); for(int j=0;j<numvex;j++){ if(side[m-1][j]>0) { num[j] = num[j] - 1; } if(num[j]==0){ stack.push(vex[j]); num[j]=-1; } } } if(a==numvex) System.out.println("拓扑排序完成"); else System.out.println("该有向图有环"); }
运行实现截图:


(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出
·此处我采用了Prim算法,即从图中某一顶点出发, 选择与它关联的具有最小权值的边,将其顶点加入到生成树顶点集合中。重复上述步骤直到所有顶点都存在于生成树顶点集合中。
主要代码:
public void primCore(MGraph graph, int v) { int visited[] = new int[graph.vertex]; visited[v] = 1; int vertex = graph.vertex; int minWeight = Prime.MAX; for (int k = 1; k < vertex; k++) { int t1 = -1; int t2 = -1; for (int i =0; i < vertex; i++) { for (int j = 0; j < vertex; j++) { boolean flag = visited[i] == 1 && visited[j] == 0 && graph.matrix[i][j] < minWeight; if (flag) { minWeight = graph.matrix[i][j]; t1 = i; t2 = j; } } } //找到一条边是最小 System.out.println("边 <" + graph.data[t1] + "," + graph.data[t2] + "> 权值:" + minWeight); visited[t2] = 1; minWeight = Prime.MAX; } }
运行结果截图:
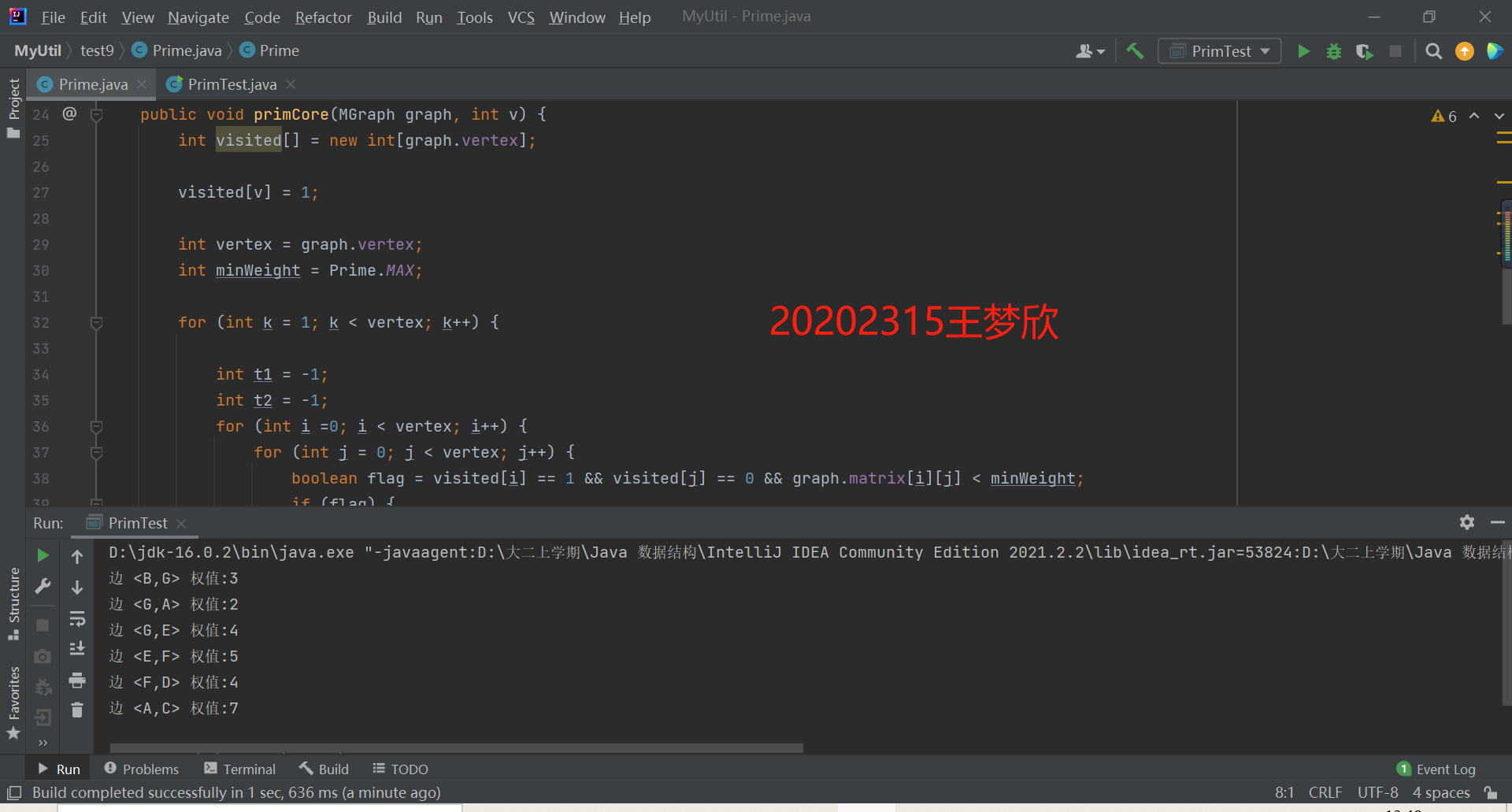
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)
以上课老师讲的有向图为例:

运行结果截图: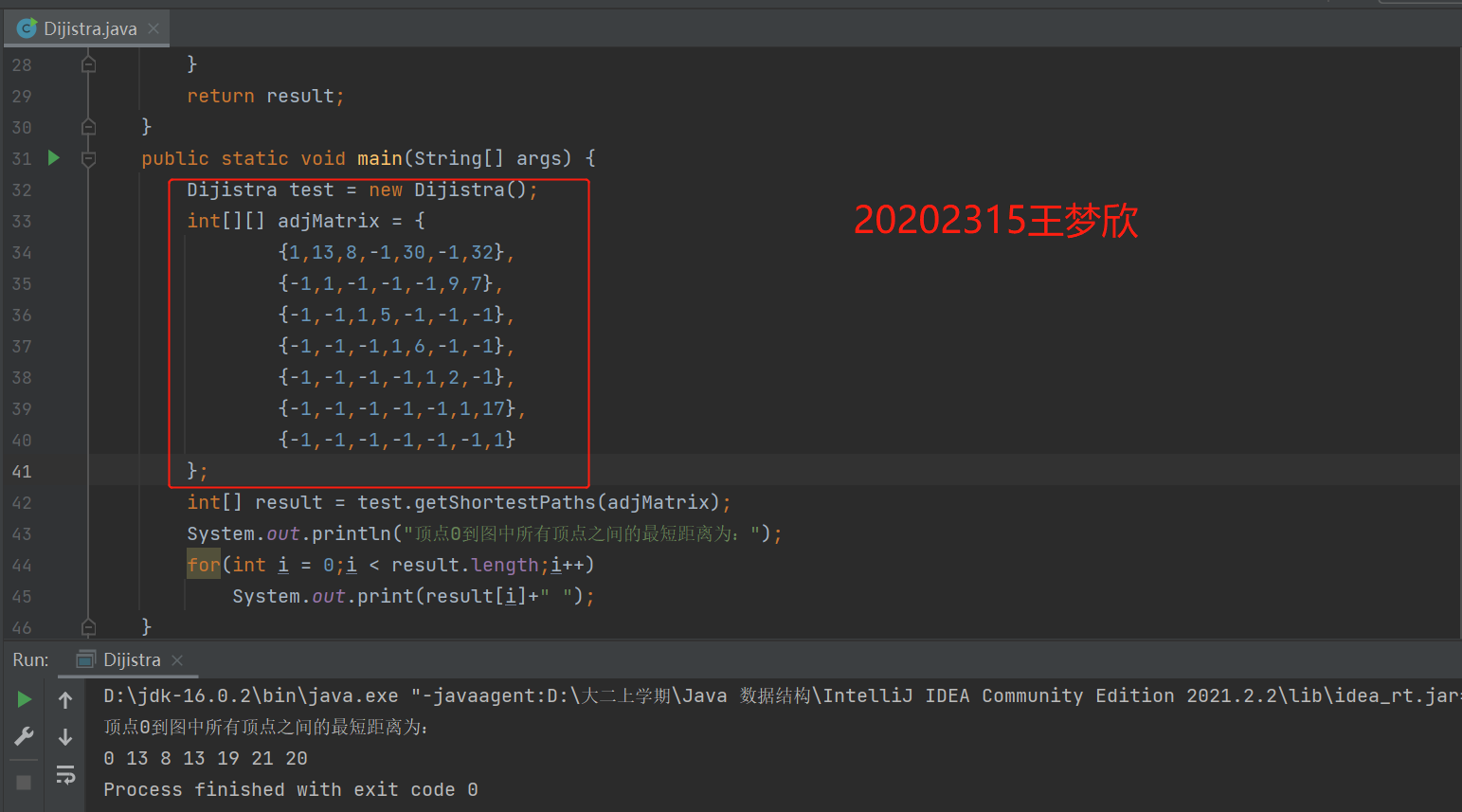
完结撒花!!!
## 其他(感悟、思考等)
磕磕绊绊中终于完成了最后一次实验报告,写完的这一刻心情好复杂啊,有松了一口气的轻松,也有一些惆怅,2020级是信管专业的最后一届,现在我们也走到了这门课程的最后,之前好多学长学姐和其他专业的同学说我们们很幸福,单单是遇上王老师这样的老师就已经是很幸福的一件事了,哈哈哈哈哈哈。
三生有幸,与恩师相识于富丰路7号,小生才疏学浅,性格顽劣,叨扰恩师多日。
愿恩师:
工作顺心
身体健康
万事胜意!
(小生以后可能还会多多叨扰恩师,望恩师见怪莫怪ღ´・ᴗ・` )





