loj6171/bzoj4899 记忆的轮廊（期望dp+优化）

题目：

https://loj.ac/problem/6171

分析：

设dp[i][j]表示从第i个点出发（正确节点），还可以有j个存档点（在i点使用一个存档机会），走到终点n的期望步数

那么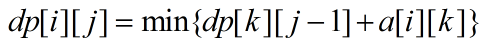

a[i][k]表示i点为存档点，从i点走到k点（正确节点）的期望步数（中间没有其它存档点）

那么a[i][j]可以递推预处理出

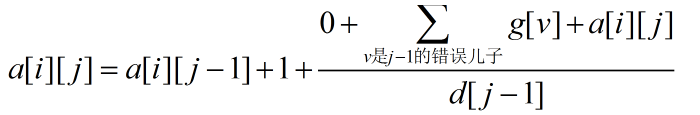
其中g[v]表示从一个错误节点v开始走，期望走g[v]步会读档

解方程可以解出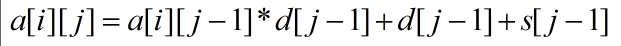

s[j-1]就是点j-1出去的所有错误儿子的g[v]之和

那么接下来只要知道如何求g[v]就行了

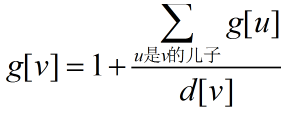
这个直接dfs一遍就行了

好，那么现在我们的主dp就可以求解了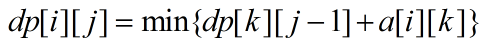

但是直接dp的复杂度是O(n^2p)的，这样会TLE

方法一：

注意到这个dp的本质是把一个序列给分成p段，那么其中某一段会不会很长呢？

我们会发现a的增长是非常快的，而最终的答案不会很大，所以也就是说当前的i的最优转移j，不会离i太远

所以通过计算可以发现这个距离step<=40

所以时间复杂度O(40n^2)

方法二：

考虑dp优化的惯用套路

容易得出此dp是决策单调的，也就是f(i)<=f(i+1)

那么就可以决策单调优化O(nplogn)

具体的就维护一个队列，队列里每个元素存着[l,r,p]表示区间l~r，当前最优决策是p

每次从队头取出最优策略，将此次新的决策从队尾开始放入并合并区间

        dp[1][n]=0.0;
        for(int now=2;now<=number;++now)
        {
            int head=1,tail=1;
            q[1]={1,n-1,n};
            for(int i=n-1;i>=1;--i)
            {
                while(head<tail&&q[head].l>i) ++head;
                dp[now][i]=cal(now-1,i,q[head].p);
                while(head<tail&&cal(now-1,q[tail].r,i)<cal(now-1,q[tail].r,q[tail].p)) --tail;
                int position=find(now,q[tail].l,q[tail].r,i,q[tail].p);
                if(position)
                {
                    q[tail+1]={1,position,i};
                    q[tail].l=position+1;
                    if(q[tail].l>q[tail].r) ++head;
                    ++tail;
                }
            }
        }

方法三：

一个很神奇的二分套路（详见王钦石《浅析一类二分方法》）

这是一个限制段数的dp，我们把它写成不限制段数的情况

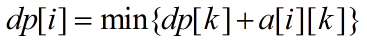
然后我们去二分一个常数C，使得式子变成这样

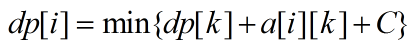
这里的C表示每次重新开一段所需要的代价

很明显，C越大，最优情况下分的段数就越少，C越小，最优情况下分的段数就越多

所以我们可以二分C，对于每个C，进行dp

通过n->pre[n]->pre[pre[n]]->...->1，我们可以知道存了多少次档，当存档数恰好等于p的时候，此时对应的划分方案就是读档p次时候的最优解，就是将dp的最优值减去C*p

但是有个trick，王钦石论文里也提到了

就是可能当前eps下，并没有哪个C会使得我恰好读了p次档，即某个C情况下，我读了p-1次档，在C-eps情况下，我读了p+1次档，就是没有读p次档

这时候有个结论就是C-eps时，我读p+1次档这个情况下也必定有我读p次档的解，此时原本答案是dp-(p+1)*C,现在这样改成读p次档之后，答案就是dp-p*C

这样复杂度是O(n^2logA)

当然这里的dp可以优化，但不过预处理的时候O(n^2)是跑不掉的，所以再优化也不会低于O(n^2)的复杂度

        int minnum=m+1;
        while (l+eps<=r)
        {
            long double mid=(l+r)/2;
            int num=check(mid);
            long double sum=0;
            for(int now=n;now!=1;now=pre[now]) sum+=w[pre[now]][now];
            if (num<=p)
            {
                if (num==p)
                {
                    ans=sum;
                    break;
                };
                r=mid-eps;
            }
            else
            {
                if(num<=minnum)
                {
                    ans=sum+(num-p)*mid;
                    minnum=num;
                }
                l=mid+eps;
            }
        }