【笔记】Tensorflow 实战Google深度学习框架

第二章 Tensorflow环境搭建

2.1 依赖包

a) Protocol Buffer：谷歌开发的处理结构化数据的工具。当要将这些结构化的用户信息持久化或者进行网络传输时，就需要先将他们进行序列化。所谓序列化，是将结构化的数据变成数据流的格式，简单地说是变成一个字符串。如何将结构化的数据序列化，并从序列化之后的数据流中还原出原来的结构化数据，统称为处理结构化数据，这就是Protocol Buffer解决的主要问题。（同样，XML和JSON也是两种比较常用的结构化数据处理工具。）

b) Bazel：谷歌开源的自动化构建工具，主要用来运行编译和测试。在一个项目空间内，Bazel通过BUILD文件来找到需要编译的目标。BUILD文件采用一种类似于Python的语法来指定每一个编译目标的输入，输出以及编译方式。与Makefile这种比较开放式的编译工具不同，Bazel的编译方式是事先定义好的。

另外关于Bazel的基本资料：https://www.cnblogs.com/Leo_wl/p/4458115.html

第三章 Tensorflow入门（基本概念）

先不讲。

第四章 深层神经网络

4.1 多层和非线性：只通过线性变换，任意层的全连接神经网络和单层神经网络模型的表达能力没有任何区别，而且他们都是线性模型。

 4.2 激活函数：将每一个神经元的输出通过一个非线性函数，那么整个神经网络的模型也就不再是线性的了，这个非线性函数就是激活函数。

神经网络的前向传播算法： y = tf.nn.relu(tf.matmul(x, w) + biase1)  ，其中使用了激活函数和偏置项。

Tensorflow也支持使用自己定义的激活函数。

4.3 损失函数：i) 交叉熵：刻画了两个概率分布之间的距离，是分类问题中使用比较广泛的一种损失函数。

如何将神经网络传播得到的结果也变成概率分布呢？Softmax回归就是一个非常常用的方法。即原始输出层-->softmax层--->最终输出层，通过softmax层将神经网络输出变成一个概率分布，假设原始的神经网络输出为y1,y2...yn，那么经过softmax回归处理之后的输出变为：

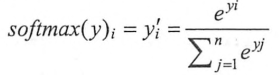，其实就是原始神经网络的输出被用作置信度来生成新的输出，而新的输出满足概率分布的所有要求。

tips：通过tf.clip_by_value()函数可以将一个张量中的数值限制在一个范围之内，这样可以避免一些运算错误（比如log0是无效的）。

因为交叉熵一般会与softmax一起使用，所以Tensorflow对这两个功能进行了统一封装，并提供了tf.nn.softmax_cross_entropy_with_logits函数。比如可以直接通过下面代码实现交叉熵损失函数：

ii) 均方误差MSE（Mean Square Error）：定义为

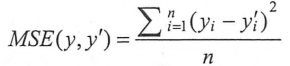，Tensorflow中实现均方误差损失函数的代码为：mse = tf.reduce_mean(tf.square(y' - y))

iii) 自定义损失函数：

通过随机数生成一个模拟数据集：

rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size, 2)

4.4 神经网络优化算法：反向传播算法和梯度下降算法

需要注意的是，梯度下降算法并不能保证被优化的函数达到全局最优解，只有当损失函数为凸函数时，梯度下降算法才能保证打达到全局最优解。

1. 不一定达到最优解，2. 训练时间长。

针对第二个问题，batch梯度下降：

batch_size = n
x = tf.placeholder(tf.float32, shape=(batch_size, 2), name='x-input')
y_ = tf.placeholder(tf.float32, shape=(batch_size, 1),name='y-input')

4.5 神经网络进一步优化

学习率：通过指数衰减的学习率即可以让模型在训练的前期快速达到较优解，又可以保证模型在训练后期不会有太大的波动，从而接近局部最优。

decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps) ，decay_rate为衰减系数，decay_steps为衰减速度。

过拟合：常用的方法是正则化，在损失函数中加入刻画模型复杂程度的指标。L1和L2正则，L1正则不可导，让参数变得稀疏；L2正则可导。

loss = tf.reduce_mean(tf.square(y_ - y)) + tf.contrib.layers.l2_regularizer(lambda)(w)

第一部分是均方差损失函数，刻画模型在训练数据上的表现；第二部分是正则化，防止模型过度训练数据中的噪音。

tips：当网络结构复杂之后定义网络结构的部分和计算损失函数的部分可能不在同一个函数中，这样通过变量这种方式计算损失函数就不方便，可以使用Tensorflow中提供的集合（collection）。

# 将均方误差损失函数加入损失集合
tf.add_to_collection('losses', mse_loss)

#将不同部分的损失函数加起来得到最终的损失函数
loss = tf.add_n(tf.get_collection('losses'))

滑动平均模型：将每一轮迭代得到的模型综合起来，从而使得最终得到的模型更加健壮（robust）

Tensorflow中提供了tf.train.ExponentialMovingAverage来实现滑动平均模型。

第五章 MNIST数字识别

 5.2 神经网络模型训练及结果

比较了使用指数衰减学习率，正则化和滑动平均三种优化来对模型进行评估，由于数据较为简单，使用这些优化得到提升不明显。

5.3 变量管理

Tensorflow提供了通过变量名称来创建或者获取一个变量的机制。通过这个机制，在不同的函数中可以直接通过变量的名字来使用变量，而不需要将变量通过参数的形式来传递。

Tensorflow中通过变量名称获取变量的机制主要是通过tf.get_variable和tf.variable_scope函数来实现。

# 下面两个定义是等价的
v = tf.get_variable("v", shape=[1], initializer=tf.constant_initializer(1.0))
v = tf.Variable(tf.constant(1.0, shape=[1]), name="v")

tips：通过tf.variable_scope函数来生成一个上下文管理器，则可以获得一个已经创建的变量：

tf.variable_scope("foo", reuse=True)

5.4 Tensorflow模型持久化

Tensorflow提供了一个API来保存和还原一个神经网络模型，这个API就是tf.train.Saver类。

# 将模型保存在/path/to/model/model.ckpt文件
saver.save(sess,"/path/to/model/model.ckpt")

在这个路径目录下会出现三个文件，因为Tensorflow会将计算图的结构和图上的参数取值分开保存。（model.ckpt.meta，保存了计算图的结构；model.ckpt保存了程序中每一个变量的取值；最后一个checkpoint文件，保存了一个目录下所有的模型文件列表）

# 加载已经保存的模型，并通过已经保存的模型中变量的值来计算
saver.restore(sess,"/path/to/model/model.ckpt")

对于要保存或加载部分变量，在声明tf.train.Saver类时可以提供一个列表来指定需要保存或者加载的变量。

# 这里声明的变量名称和已经保存模型中变量名称不同
v1 = tf.Variable(tf.constant(1.0, shape=[1]), name='other-v1')
v2 = tf.Variable(tf.constant(1.0, shape=[1]), name='other-v2')
#原来名称为v1的变量现在加载到变量v1中（名称为other-v1），名称为v2的变量加载到变量v2中（名称为other-v2）
saver = tf.train.Saver({"v1":v1, "v2":v2})

在这个程序中，对变量v1和v2的名称进行了修改。如果直接通关tf.train.Saver默认的构造函数来加载保存的模型，那么程序会报变量找不到的错误。因为保存时候的变量名称和加载时的变量名称不一致。为了解决这个问题，Tensorflow可以通过字典（dictionary）将模型保存时的变量名和需要加载时的变量联系起来。

tips：使用tf.train.Saver会保存运行Tensorflow程序所需要的全部信息，然后有时并不需要某些信息（类似变量初始化，模型保存等辅助节点信息），于是Tensorflow提供了convert_variables_to_constants函数，通过这个函数可以将计算图中的变量及其取值通过常量的方式保存。

with tf.Session() as sess:
    sess.run(init_op)
    #导出当前计算图的GraphDef部分，只需要这部分就可以完成从输入层到输出层的计算过程
    graph_def = tf.get_default_graph().as_graph_def()
    output_graph_def = graph_util.convert_variables_to_constants(sess, graph_def, ['add'])
    #将导出的模型存入文件
    with tf.gfile.Gfile("/path/to/model/combined_model.pb","wb") as f:
        f.write(output_graph_def.SerializeToString())

with tf.Session() as sess:
　　model_filename = "/path/to/model/combined_model.pb"
　　with gfile.FastGfile(model_filename,'rb') as f:
　　　　graph_def = tf.GraphDef()
　　　　graph_def.ParseFromString(f.read())

　　result = tf.import_graph_def(graph_def, return_elements=["add:0"])
　　print(sess.run(result)

关于持久化原理及数据格式，未看，先跳过。。

5.5 Tensorflow最佳样例

在训练的过程中每隔一段时间保存一次模型训练中的中间结果。

# 保存当前的模型，这里给出global_step参数，这样可以让保存模型的文件名末尾加上训练的轮数
saver.save(sess, os.path.join(MODEL_SAVE_PATH,MODEL_NAME), global_step=global_step)

##题外话，keras中可以让loss更小（模型更优）的时候就保存
from keras.callbacks import ModelCheckpoint
model_checkpoint = ModelCheckpoint(check_point_path, monitor='loss', verbose=1, save_best_only=True)
self.model.save_weights(self.path,overwrite=True)

测试代码：

with tf.Session() as sess:
    #tf.train.get_checkpoint_state函数会通过checkpoint文件自动找到目录中最新模型的文件名
    ckpt = tf.train.get_checkpoint_state(mnist_train.MODEL_SAVE_PATH)
    if ckpt and ckpt.model_checkpoint_path:
        #加载模型
        saver.restore(sess, ckpt.model_checkpoint_path)
            

第六章 图像识别与卷积神经网络
卷积神经网络和全连接神经网络（即输入矩阵大小和过滤器尺寸大小一样）的唯一区别就在于神经网络中相邻两层的连接方式。全连接参数过多，导致计算速度变慢，而且容易导致过拟合。在神经网络中，每一个卷积层中使用的过滤器中的参数都是一样的。以数字"1"为例，无论数字1出现在图像中的左上角还是右下角，图片的种类都是不变的，因为左上角和右下角使用的过滤器参数相同，通过卷积层后无论数字在图像中的哪个位置，得到的结构都是一样。以cifar10为例，输入层的矩阵维度是32x32x3，假设第一层卷积层使用的尺寸是5x5，深度为16的过滤器，那么这个卷积层的参数个数为5x5x3x16+16=1216个。卷积层的参数个数和图片大小无关，只和过滤器的尺寸，深度和当前层节点矩阵的深度有关。

#第三个参数为不同维度上的步长，第一个和最后一个数字要求一定是1，因为卷积层的步长只对矩阵的长和宽有效。还是不懂，大佬们知道的告诉下。。
conv = tf.nn.conv2d(input, filter_weight, stride=[1,1,1,1], padding='SAME')

池化层：卷积层和池化层中过滤器移动方式是相似的，唯一的区别在于卷积层使用的过滤器是横跨整个深度的，而池化层使用的过滤器只影响一个深度上的节点。所以池化层的过滤器除了在长和宽两个维度移动之外，它还需要在深度这个维度上移动。

#ksize中第一个和最后一个数字必须为1，这意味着池化层的过滤器是不可以跨不同输入样例或者节点矩阵深度的。其中strides中第一个和最后一个也只能为1，这意味着池化层不能减少节点矩阵
的深度或者输入样例的个数。还是不懂。。
pool = tf.nn.max_pool(activated_conv, ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')

#全连接层需要的输入格式为向量，所以这里需要将前一层得到的矩阵拉直成一个向量。get_shape函数可以直接得到矩阵的维度
pool_shape = pool2.get_shape().as_list()
#计算将矩阵拉直成向量之后的长度，这个长度就是矩阵长宽和深度的乘积
#这里pool_shape[0]为一个batch中数据的个数
nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
#通过tf.reshape函数将第四层的输出变成一个batch的向量
reshaped=tf.reshape(pool2, [pool_shape[0], nodes])
#后面加入dropout，一般只在全连接层而不是卷积层或池化层使用（train）
if train:
    fc1 = tf.nn.dropout(fc1, 0.5)

Inception模型：将不同的卷积层通过并联的方式结合在一起。虽然过滤器的尺寸不同，但如果所有的过滤器都使用全0填充且步长为1，那么前向传播得到的结果矩阵的长和宽都与输入矩阵一致，这样经过不同过滤器处理的结果矩阵可以拼接成一个更深的矩阵。

#tf.concat函数可以将多个矩阵拼接起来，第一个参数指定拼接的维度，第二个指定要拼接的矩阵列表
net = tf.concat(3, [branch_0, branch_1, branch_2, branch_3])

迁移学习finetune：只替换最后一层连接层，并将在最后这一层全连接层之前的网络层称之为瓶颈层（bottleneck）。因为将瓶颈层的输出再通过一个单层的全连接层神经网络可以很好的区分1000种类别的图像，所有有理由认为瓶颈层输出的节点向量可以被作为任何图像的一个更加精简且表达能力更强的特征向量。于是在新数据集上，可以直接利用这个训练好的神经网络对图像进行特征提取，然后再将提取到的特征向量作为输入来训练一个单层全连接层神经网络处理新的分类问题。

第七章 图像数据处理

继续。。

 第十章 Tensorflow计算加速

10.1 Tensorflow使用GPU：Tensorflow程序通过tf.device函数来指定运行每一个操作的设备，这个设备可以是本地的CPU或者GPU，也可以是某一台远程的服务器。

Tensorflow提供在生成会话时，可以设置log_device_placement参数来打印运行每一个运算的设备，如下：

#通过log_device_placement参数来输出运行每一个运算的设备
sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))

在配置好GPU环境的Tensorflow中，如果操作没有明确指定运行设备，那么Tensorflow会优先选择GPU。默认情况下，如果有多个GPU，Tensorflow只会将运算优先放在/gpu:0上。如果需要将某些运算放到不同的GPU或者CPU上，就需要通过tf.device来手工指定，如下代码：

import tensorflow as tf
#通过tf.device将运算指定到特定的设备上
with tf.device('/cpu:0'):
    a = tf.constant([1.0,2.0,3.0], shape=[3], name='a')
    b = tf.constant([1.0,2.0,3.0], shape=[3], name='b')
with tf.device('/gpu:1'):
    c = a + b
sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))
print(sess.run(c))

在GPU上，tf.Variable操作只支持实数型（float16，float32和double）的参数，int则不支持。为避免这个问题，Tensorflow在生成会话时可以指定allow_soft_placement参数。当allow_soft_placement参数设置为True时，如果运算无法由GPU执行，那么Tensorflow会自动将它放到CPU上执行。

GPU是机器中相对独立的资源，将计算放入或者转出GPU都需要额外的时间，而且GPU需要将计算时需要用到的数据从内存复制到GPU设备上，这也需要额外的时间。

10.2 深度学习训练并行模式：常用的并行化深度学习模式训练方式有两种：同步模式和异步模式

在并行化地训练深度学习模型时，不同设备（CPU或GPU）可以在不同训练数据上运行这个迭代的过程，而不同并行模式的区别在于在反向传播算法中不同的参数更新方式。

异步模式：在每一轮迭代时，不同设备会读取参数最新的取值，但因为不同设备读取参数取值的时间不一样，所以得到的值也有可能不一样。根据当前参数的取值和随机获取的一小部分训练数据，不同设备各自运行反向传播的过程独立地更新参数。可以简单认为异步模式就是单机模式复制了多份，每一份使用不同的训练数据进行训练，在异步模式下，不同设备之间是完全独立的。（注：使用异步模式训练的深度学习模型有可能无法达到较优的训练效果。）

同步模式：所有的设备同时读取参数的取值，并且当反向传播算法完成之后同步更新参数的取值。单个设备不会单独对参数进行更新，而会等待所有设备都完成反向传播之后再统一更新参数。在每一轮迭代时，虽然所有设备使用的参数是一致的，但是因为训练数据不同，所以得到参数的梯度就可能不一样。当所有设备完成反向传播计算之后，需要计算出不同设备上参数梯度的平均值，最后再根据平均值对参数进行更新。

虽然同步模式解决了异步模式中存在的参数更新问题，然后同步模式的效率却低于异步模式。如果设备的运行速度不一致，那么每一轮训练都需要等待最慢的设备结束后才能开始更新参数，于是很多时间都花在等待上。虽然理论上异步模式存在缺陷，但是训练深度学习模型时使用的随机梯度下降算法本身就是梯度下降的一个近似算法，即使是梯度下降也无法保证达到全局最优值。若多个GPU性能相似，一般则采用同步模式训练深度学习模型。

10.3 多GPU并行

10.4 分布式Tensorflow