test-2019-5-6
T1 ZYB建围墙
题目大意:求在六边形网格里围住至少n个格子的最短围墙长度
数据范围:
solution
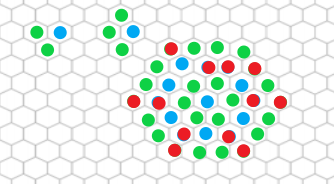
结合图片,40分可以手推出来,然后找到规律:最优解一定是朝着正六边形的形状分布的:
每一步基于的最优的情况下,应该尽量制造出如左上角第二个图的绿点所示的情况,(因为这样下一步就和上一步的花费相同了),否则是左上角的第一种情况,(比上一步的答案多1),
我们可以枚举求出对于当前的点数n里面的正六边形的边长x,然后发现对于外面再加一层的情况来说,总共有6段,第1段有x-1个点,第2~5段各有x个点,第6段有x+1个点,每一段都是第一个点+1(拐角只能是第一种情况),后面都是+0(围成了第二种情况), 模拟即可
T2 ZYB和售货机
题目大意
solution:
-
注意到总共n个点,n条边,则整个图为一个内向基环树(所有i都只有一个fa[i],从i到fa[i]连边,则树上的边都朝向环
-
边(x,y)的含义为:
如果x还没有被取完,那么y可以被取任意个(产生num*(sell[y]-buy[x])的收益)
整张图应该是一个基环树森林的形态 -
对于树上的边,显然都可以取(先取父亲再取儿子)
-
对于环上的边
可以发现,
1.如果存在一个环上的点i,通过i来买f[i]的收益比连向f[i]的另外一条树边还小,
不如将这条边断开;
2.而如果不存在这样的i,则环上的点就都是最优的 ,我们可以先把环上的物品取到每个都只剩一个,
此时注意到会有一个物品取不到环边的价值,那么我们就找一个环边价值和树边价值的差最小的点,强制它不能选择环边 -
实际上,我们只要记录到每个节点的最大和次大的边
DFS 过程中,默认接上最大边的值,维护最大边和次大边的差的最小值
找到环之后,我们显然要断掉环——使连向某个点的边改变(从默认的最大变成次大),此时只要减去维护的最小值即可
T3 ZYB玩字符串
题目大意:
soluition
- 暴力\(O(len^2)\)枚举答案,暴力check(尝试能不能拼出来)可得40
- 枚举过程无法优化,但是check可以:
- dp过程可以记忆化也可以按区间dp写(石子合并)







