[回归分析][7]--定性预测变量
[回归分析][7]--定性预测变量
这一篇文章将讲一类特殊的变量。(0--1变量)
如可以表示 性别(男/女),季节(4个季节需要三个变量)
我们来看一个具体用法的例子。
*——————————下面是例子————————*
有三个年限1960,1970,1975
现在考虑人均教育支出在每个年份是否有显著差异。

是不是感觉很熟悉,和前面一篇文章的F检验差不多,确实,这里的问题在于全模型(FM)构造。

T1和T2是预测变量
则全模型为
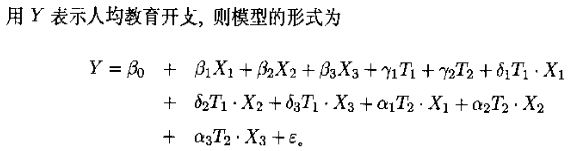
每一个定性变量都会 Y1*T1 , Y2*T1,表示T1对斜率个截距的改变量。
RM:Y = B0+B1*X1+B2*X2+B3*X3
下面给出数据
然后就是和拟合方程。构造F值,计算是否有显著区别
(注意:做了一次回归之后要检查回归的是否好,看看有没有异常点,把异常点去掉后重新再回归一次)
这张图表示是有异常点的
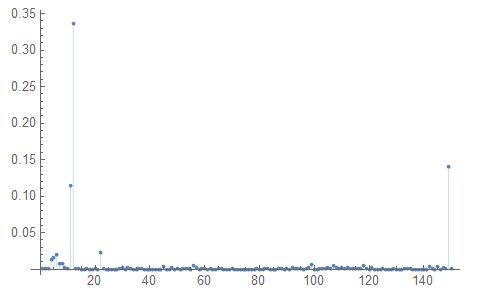
去掉后做回归
FM:

看一下R^2
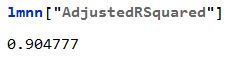
说明我们回归得还可以
RM:

这是RM的方差表
计算p值

如可以表示 性别(男/女),季节(4个季节需要三个变量)
我们来看一个具体用法的例子。
*——————————下面是例子————————*
有三个年限1960,1970,1975
现在考虑人均教育支出在每个年份是否有显著差异。
是不是感觉很熟悉,和前面一篇文章的F检验差不多,确实,这里的问题在于全模型(FM)构造。
T1和T2是预测变量
则全模型为
每一个定性变量都会 Y1*T1 , Y2*T1,表示T1对斜率个截距的改变量。
RM:Y = B0+B1*X1+B2*X2+B3*X3
下面给出数据
{data1960, data1970,
data1975} = {{{61, 1704, 388, 399, 1, 1960, -1, 1, 0}, {68, 1885,
372, 598, 1, 1960, -1, 1, 0}, {72, 1745, 397, 370, 1, 1960, -1,
1, 0}, {72, 2394, 358, 868, 1, 1960, -1, 1, 0}, {62, 1966, 357,
899, 1, 1960, -1, 1, 0}, {91, 2817, 362, 690, 1, 1960, -1, 1,
0}, {104, 2685, 341, 728, 1, 1960, -1, 1, 0}, {99, 2521, 353,
826, 1, 1960, -1, 1, 0}, {70, 2127, 352, 656, 1, 1960, -1, 1,
0}, {82, 2184, 387, 674, 2, 1960, -1, 1, 0}, {834, 1990, 392,
568, 2, 1960, -1, 1, 0}, {834, 2435, 366, 759, 2, 1960, -1, 1,
0}, {104, 2099, 403, 650, 2, 1960, -1, 1, 0}, {84, 1936, 393,
621, 2, 1960, -1, 1, 0}, {103, 1916, 402, 610, 2, 1960, -1, 1,
0}, {86, 1863, 385, 522, 2, 1960, -1, 1, 0}, {69, 2037, 364, 613,
2, 1960, -1, 1, 0}, {94, 1697, 429, 351, 2, 1960, -1, 1,
0}, {79, 1644, 411, 390, 2, 1960, -1, 1, 0}, {80, 1894, 379, 520,
2, 1960, -1, 1, 0}, {98, 2001, 380, 564, 2, 1960, -1, 1,
0}, {124, 2760, 388, 326, 3, 1960, -1, 1, 0}, {92, 2221, 393,
562, 3, 1960, -1, 1, 0}, {67, 1674, 402, 487, 3, 1960, -1, 1,
0}, {66, 1509, 405, 358, 3, 1960, -1, 1, 0}, {65, 1384, 423, 362,
3, 1960, -1, 1, 0}, {57, 1218, 453, 343, 3, 1960, -1, 1,
0}, {60, 1487, 420, 498, 3, 1960, -1, 1, 0}, {74, 1876, 334, 628,
3, 1960, -1, 1, 0}, {49, 1397, 594, 377, 3, 1960, -1, 1,
0}, {60, 1439, 346, 457, 3, 1960, -1, 1, 0}, {59, 1359, 637, 517,
3, 1960, -1, 1, 0}, {68, 1053, 448, 362, 3, 1960, -1, 1,
0}, {56, 1225, 403, 416, 3, 1960, -1, 1, 0}, {72, 1576, 433, 562,
3, 1960, -1, 1, 0}, {80, 1740, 378, 610, 3, 1960, -1, 1,
0}, {79, 1814, 409, 727, 3, 1960, -1, 1, 0}, {95, 1920, 412, 463,
4, 1960, -1, 1, 0}, {79, 1701, 418, 414, 4, 1960, -1, 1,
0}, {142, 2088, 415, 568, 4, 1960, -1, 1, 0}, {108, 2047, 399,
621, 4, 1960, -1, 1, 0}, {94, 1838, 458, 618, 4, 1960, -1, 1,
0}, {107, 1932, 425, 699, 4, 1960, -1, 1, 0}, {109, 1753, 494,
665, 4, 1960, -1, 1, 0}, {114, 2569, 372, 663, 4, 1960, -1, 1,
0}, {112, 2160, 386, 584, 4, 1960, -1, 1, 0}, {105, 2006, 382,
534, 4, 1960, -1, 1, 0}, {129, 2557, 373, 717, 4, 1960, -1, 1,
0}, {107, 1900, 434, 379, 4, 1960, -1, 1, 0}, {77, 1852, 431,
693, 4, 1960, -1, 1, 0}}, {{189, 2828, 351, 508, 1, 1970, 0, 0,
1}, {169, 3259, 346, 564, 1, 1970, 0, 0, 1}, {230, 3072, 348,
322, 1, 1970, 0, 0, 1}, {168, 3835, 335, 846, 1, 1970, 0, 0,
1}, {180, 3549, 327, 871, 1, 1970, 0, 0, 1}, {193, 4256, 341,
774, 1, 1970, 0, 0, 1}, {261, 4151, 326, 856, 1, 1970, 0, 0,
1}, {214, 3954, 333, 889, 1, 1970, 0, 0, 1}, {201, 3419, 326,
715, 1, 1970, 0, 0, 1}, {172, 3509, 354, 753, 2, 1970, 0, 0,
1}, {194, 3412, 359, 649, 2, 1970, 0, 0, 1}, {189, 3981, 349,
830, 2, 1970, 0, 0, 1}, {233, 3675, 369, 738, 2, 1970, 0, 0,
1}, {209, 3363, 361, 659, 2, 1970, 0, 0, 1}, {262, 3341, 365,
664, 2, 1970, 0, 0, 1}, {234, 3265, 344, 572, 2, 1970, 0, 0,
1}, {177, 3257, 336, 701, 2, 1970, 0, 0, 1}, {177, 2730, 369,
443, 2, 1970, 0, 0, 1}, {187, 2876, 369, 446, 2, 1970, 0, 0,
1}, {148, 3239, 350, 615, 2, 1970, 0, 0, 1}, {196, 3303, 340,
661, 2, 1970, 0, 0, 1}, {248, 3795, 376, 722, 3, 1970, 0, 0,
1}, {247, 3742, 364, 766, 3, 1970, 0, 0, 1}, {180, 3068, 353,
631, 3, 1970, 0, 0, 1}, {149, 2470, 329, 390, 3, 1970, 0, 0,
1}, {155, 2664, 354, 450, 3, 1970, 0, 0, 1}, {149, 2380, 377,
476, 3, 1970, 0, 0, 1}, {156, 2781, 371, 603, 3, 1970, 0, 0,
1}, {191, 3191, 336, 805, 3, 1970, 0, 0, 1}, {140, 2645, 349,
523, 3, 1970, 0, 0, 1}, {137, 2579, 343, 588, 3, 1970, 0, 0,
1}, {112, 2337, 362, 584, 3, 1970, 0, 0, 1}, {130, 2081, 385,
445, 3, 1970, 0, 0, 1}, {134, 2322, 352, 500, 3, 1970, 0, 0,
1}, {162, 2634, 390, 661, 3, 1970, 0, 0, 1}, {135, 2880, 330,
680, 3, 1970, 0, 0, 1}, {155, 3029, 369, 797, 3, 1970, 0, 0,
1}, {238, 2942, 369, 534, 4, 1970, 0, 0, 1}, {170, 2668, 368,
541, 4, 1970, 0, 0, 1}, {238, 3190, 366, 605, 4, 1970, 0, 0,
1}, {192, 3340, 358, 785, 4, 1970, 0, 0, 1}, {227, 2651, 421,
698, 4, 1970, 0, 0, 1}, {207, 3027, 387, 796, 4, 1970, 0, 0,
1}, {201, 2790, 412, 804, 4, 1970, 0, 0, 1}, {225, 3957, 385,
809, 4, 1970, 0, 0, 1}, {215, 3688, 342, 726, 4, 1970, 0, 0,
1}, {233, 3317, 333, 671, 4, 1970, 0, 0, 1}, {273, 3968, 348,
909, 4, 1970, 0, 0, 1}, {372, 4146, 440, 484, 4, 1970, 0, 0,
1}, {212, 3513, 383, 831, 4, 1970, 0, 0, 1}}, {{235, 3944, 325,
508, 1, 1975, 1, 0, 0}, {231, 4578, 323, 564, 1, 1975, 1, 0,
0}, {270, 4011, 328, 322, 1, 1975, 1, 0, 0}, {261, 5233, 305,
846, 1, 1975, 1, 0, 0}, {300, 4780, 303, 871, 1, 1975, 1, 0,
0}, {317, 5889, 307, 774, 1, 1975, 1, 0, 0}, {387, 5663, 301,
856, 1, 1975, 1, 0, 0}, {285, 5759, 310, 889, 1, 1975, 1, 0,
0}, {300, 4894, 300, 715, 1, 1975, 1, 0, 0}, {221, 5012, 324,
753, 2, 1975, 1, 0, 0}, {264, 4908, 329, 649, 2, 1975, 1, 0,
0}, {308, 5753, 320, 830, 2, 1975, 1, 0, 0}, {379, 5439, 337,
738, 2, 1975, 1, 0, 0}, {342, 4634, 328, 659, 2, 1975, 1, 0,
0}, {378, 4921, 330, 664, 2, 1975, 1, 0, 0}, {232, 4869, 318,
572, 2, 1975, 1, 0, 0}, {231, 4672, 309, 701, 2, 1975, 1, 0,
0}, {246, 4782, 333, 443, 2, 1975, 1, 0, 0}, {230, 4296, 330,
446, 2, 1975, 1, 0, 0}, {268, 4827, 318, 615, 2, 1975, 1, 0,
0}, {337, 5057, 304, 661, 2, 1975, 1, 0, 0}, {344, 5540, 328,
722, 3, 1975, 1, 0, 0}, {330, 5331, 323, 766, 3, 1975, 1, 0,
0}, {261, 4715, 317, 631, 3, 1975, 1, 0, 0}, {214, 3828, 310,
390, 3, 1975, 1, 0, 0}, {245, 4120, 321, 450, 3, 1975, 1, 0,
0}, {233, 3817, 342, 476, 3, 1975, 1, 0, 0}, {250, 4243, 339,
603, 3, 1975, 1, 0, 0}, {243, 4647, 287, 805, 3, 1975, 1, 0,
0}, {216, 3967, 325, 523, 3, 1975, 1, 0, 0}, {212, 3946, 315,
588, 3, 1975, 1, 0, 0}, {208, 3724, 332, 584, 3, 1975, 1, 0,
0}, {215, 3448, 358, 445, 3, 1975, 1, 0, 0}, {221, 3680, 320,
500, 3, 1975, 1, 0, 0}, {244, 3825, 355, 661, 3, 1975, 1, 0,
0}, {234, 4189, 306, 680, 3, 1975, 1, 0, 0}, {269, 4336, 335,
797, 3, 1975, 1, 0, 0}, {302, 4418, 335, 534, 4, 1975, 1, 0,
0}, {268, 4323, 344, 541, 4, 1975, 1, 0, 0}, {323, 4813, 331,
605, 4, 1975, 1, 0, 0}, {304, 5046, 324, 785, 4, 1975, 1, 0,
0}, {317, 3764, 366, 698, 4, 1975, 1, 0, 0}, {332, 4504, 340,
796, 4, 1975, 1, 0, 0}, {315, 4005, 378, 804, 4, 1975, 1, 0,
0}, {291, 5560, 330, 809, 4, 1975, 1, 0, 0}, {312, 4989, 313,
726, 4, 1975, 1, 0, 0}, {316, 4697, 305, 671, 4, 1975, 1, 0,
0}, {332, 5438, 307, 909, 4, 1975, 1, 0, 0}, {546, 5613, 386,
484, 4, 1975, 1, 0, 0}, {311, 5309, 333, 831, 4, 1975, 1, 0,
0}}};然后就是和拟合方程。构造F值,计算是否有显著区别
(注意:做了一次回归之后要检查回归的是否好,看看有没有异常点,把异常点去掉后重新再回归一次)
这张图表示是有异常点的
去掉后做回归
FM:
看一下R^2
说明我们回归得还可以
RM:
这是RM的方差表
计算p值
可以看到p值较小,故拒绝原假设,所以教育经费改变了,应该要加上定性变量来拟合。
再看一张图

这个是按年位横座标的残差图,可以看到残差是在0的上下的,有三个异常数据点
以上,所有
2016/11/4
再看一张图
这个是按年位横座标的残差图,可以看到残差是在0的上下的,有三个异常数据点
以上,所有
2016/11/4


