[回归分析][8]--变量的变换
[回归分析][8]--变量的变换
这一节会讲关于变量的变换,如最常用的(做对数变换),和我们在什么情况下要做变换。
当然,要能做变换,我们必须要熟悉函数的形状,下面给出常见函数的图像。
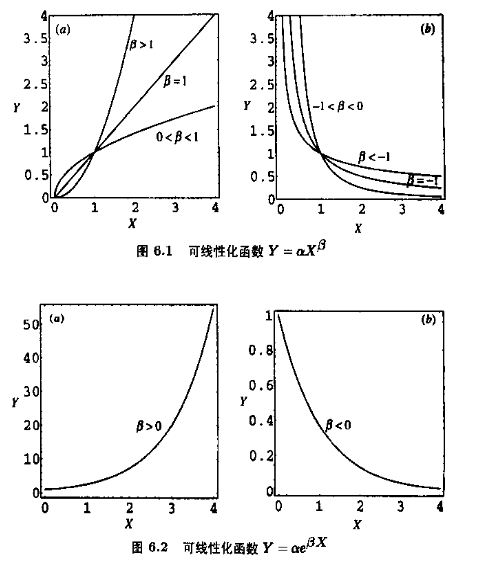
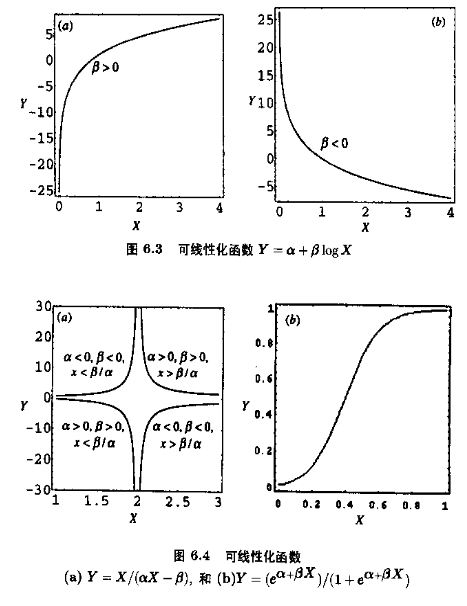
(其实,当我们能由函数图像猜出函数式子的时候,可以使用非线性回归)
我们这里使用变换来做,看一个例子
这是一组年份与石油产量的数据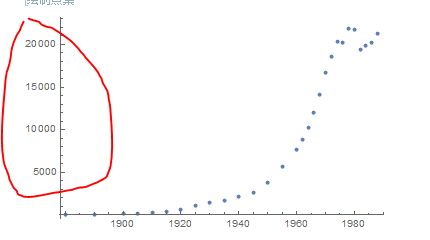
由散点图可以看出,y轴是呈现10的倍数的增长的,所以我们考虑对y取Log
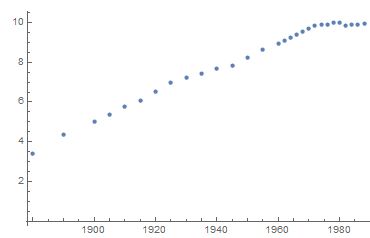
这时再画图可以看出形状接近一条直线了。接下来就可以把Y = Log[y]看成一个新的变量来处理了,方法还是和之前的一样。
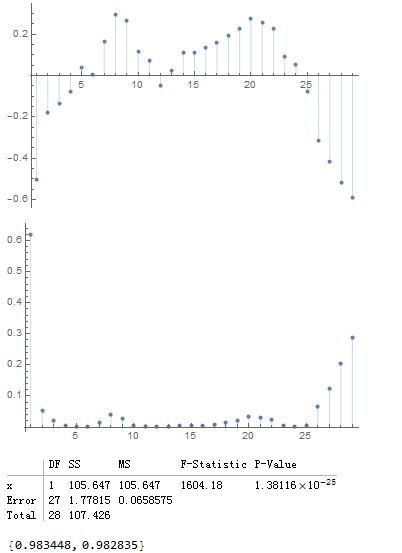
如上图,可以依次得到1.残差图 2.库克距离 3.方差表 4.R^2
以上,所有
2016/11/14
当然,要能做变换,我们必须要熟悉函数的形状,下面给出常见函数的图像。
(其实,当我们能由函数图像猜出函数式子的时候,可以使用非线性回归)
我们这里使用变换来做,看一个例子
这是一组年份与石油产量的数据
data = {{1880, 30}, {1890, 77}, {1900, 149}, {1905, 215}, {1910,
328}, {1915, 432}, {1920, 689}, {1925, 1069}, {1930, 1412}, {1935,
1655}, {1940, 2150}, {1945, 2595}, {1950, 3803}, {1955,
5626}, {1960, 7674}, {1962, 8882}, {1964, 10310}, {1966,
12016}, {1968, 14104}, {1970, 16690}, {1972, 18584}, {1974,
20389}, {1976, 20188}, {1978, 21922}, {1980, 21722}, {1982,
19411}, {1984, 19837}, {1986, 20246}, {1988, 21338}};由散点图可以看出,y轴是呈现10的倍数的增长的,所以我们考虑对y取Log
ListPlot[Transpose[{data[[All, 1]], Log[data[[All, 2]]]}]]这时再画图可以看出形状接近一条直线了。接下来就可以把Y = Log[y]看成一个新的变量来处理了,方法还是和之前的一样。
datan = Transpose[{data[[All, 1]], N[Log[data[[All, 2]]]]}];
lm = LinearModelFit[datan, x, x];
cc = lm["FitResiduals"];
cook = lm["CookDistances"];
ListPlot[cc, Filling -> Axis, PlotRange -> All]
ListPlot[cook, Filling -> Axis, PlotRange -> All]
lm["ANOVATable"]
lm[{"RSquared", "AdjustedRSquared"}]如上图,可以依次得到1.残差图 2.库克距离 3.方差表 4.R^2
以上,所有
2016/11/14


