[回归分析][12]--主成分分析
[回归分析][12]--主成分分析
这一篇文章会讲一下关于主成分的内容,这里就是处理数据间有相关性的。
我会用一个例子来说明:
(*1.对原始数据进行回归*)
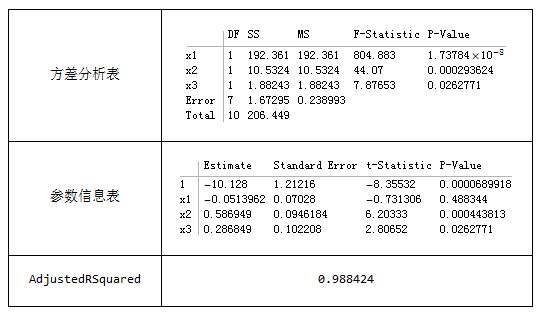
(*2.对标准化后的数据进行回归*)
(*3.计算相关矩阵的特征值 特征向量 条件数=Sqrt[最大特征跟/最小特征跟]*)

条件数:
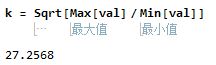
(*4.构建新的变量 主成分c = x.v'*)
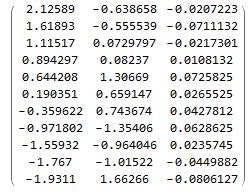
(*5.对c进行回归,回归的时候去掉特征值小的对应的c---切记要用标准化的数据*)
我们考虑--留两个主成分
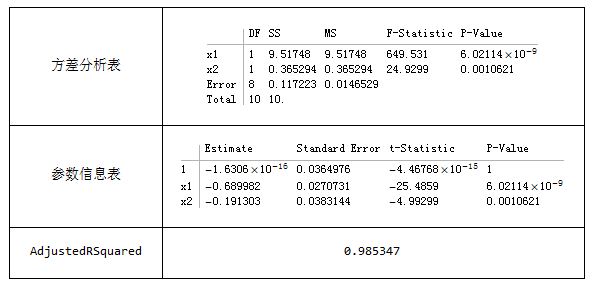
再看一下条件数:

可以看到条件数变成了1,说明变好了。
更加详细的可以看代码,代码已经上传了,下载链接如下:
代码下载链接
以上,所有
2016/12/9
这一篇文章会讲一下关于主成分的内容,这里就是处理数据间有相关性的。
我会用一个例子来说明:
data = {{49.`, 15.9`, 149.3`, 4.2`, 108.1`}, {50.`, 16.4`, 161.2`,
4.1`, 114.8`}, {51.`, 19.`, 171.5`, 3.1`, 123.2`}, {52.`, 19.1`,
175.5`, 3.1`, 126.9`}, {53.`, 18.8`, 180.8`, 1.1`, 132.1`}, {54.`,
20.4`, 190.7`, 2.2`, 137.7`}, {55.`, 22.7`, 202.1`, 2.1`,
146.`}, {56.`, 26.5`, 212.4`, 5.6`, 154.1`}, {57.`, 28.1`, 226.1`,
5.`, 162.3`}, {58.`, 27.6`, 231.9`, 5.1`, 164.3`}, {59.`, 26.3`,
239.`, 0.7`, 167.6`}};上面是这次会用到的数据(*1.对原始数据进行回归*)
lm1 = LinearModelFit[data, {x1, x2, x3}, {x1, x2, x3}]
Grid[{{"方差分析表", lm1["ANOVATable"]}, {"参数信息表",
lm1["ParameterTable"]}, {"AdjustedRSquared",
lm1["AdjustedRSquared"]}}, Spacings -> {3, 3}, Frame -> All](*2.对标准化后的数据进行回归*)
datastand = Standardize[data];
lm2 = LinearModelFit[datastand, {x1, x2, x3}, {x1, x2, x3}];
Grid[{{"方差分析表", lm2["ANOVATable"]}, {"参数信息表",
lm2["ParameterTable"]}, {"AdjustedRSquared",
lm2["AdjustedRSquared"]}}, Spacings -> {3, 3}, Frame -> All](*3.计算相关矩阵的特征值 特征向量 条件数=Sqrt[最大特征跟/最小特征跟]*)
mat = Correlation[data[[All, {1, 2, 3}]]];
eig = Eigenvectors[mat]
相关系数矩阵:条件数:
(*4.构建新的变量 主成分c = x.v'*)
c = datastand[[All, {1, 2, 3}]].Transpose[eig]
(*5.对c进行回归,回归的时候去掉特征值小的对应的c---切记要用标准化的数据*)
我们考虑--留两个主成分
c2 = c[[All, {1, 2}]];
c2 = Transpose[c2];
data52 = Transpose[AppendTo[c2, datastand[[All, -1]]]];
lm52 = LinearModelFit[data52, {x1, x2}, {x1, x2}]
Grid[{{"方差分析表", lm52["ANOVATable"]}, {"参数信息表",
lm52["ParameterTable"]}, {"AdjustedRSquared",
lm52["AdjustedRSquared"]}}, Spacings -> {3, 3}, Frame -> All]再计算标准化情况下的参数和原始数据的参数stdxs = Transpose[eig].{-0.689, -0.191, 0};
{b1, b2, b3} = (StandardDeviation[data[[All, -1]]]/
StandardDeviation[data[[All, #]]])*stdxs[[#]] & /@ {1, 2, 3}
Mean[data[[All, -1]]] - b1*Mean[data[[All, 1]]] -
b2*Mean[data[[All, 2]]] - b3*Mean[data[[All, 3]]]再看一下条件数:
可以看到条件数变成了1,说明变好了。
更加详细的可以看代码,代码已经上传了,下载链接如下:
代码下载链接
以上,所有
2016/12/9


