[回归分析][13]--岭回归
[回归分析][13]--岭回归
这一次讲一下用mathematica来做岭回归。
岭回归的作用也是为了消除变量间的相关性的。
说一下步骤:
1.先对数据进行长度单位化(即均值为0,长度为1)
2.构造新的变量,如:
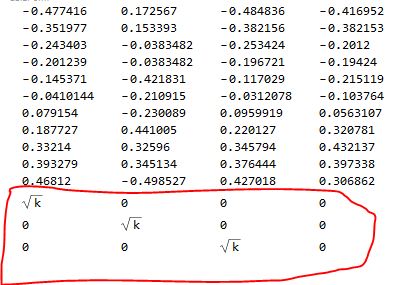
3.对新的变量做普通最小二乘,画出岭迹图,确定k(0<k<1)。
4.系数转化
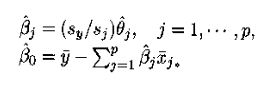
例子:
下面为这次例子的数据
1.对数据长度单位化
2.构造新的变量
3.画出岭迹图,确定k
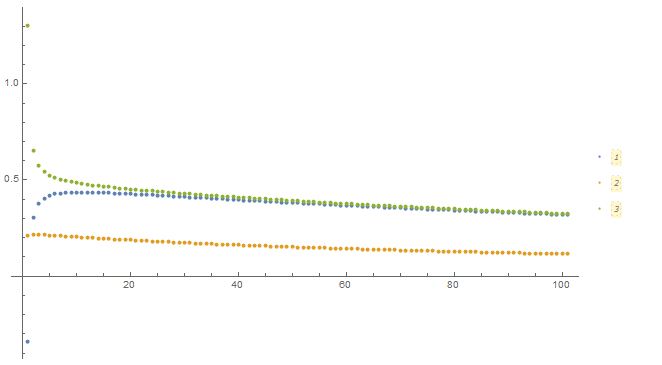
可以看到大概在第四点后开始平稳,即k=0.04
4.计算原系数

以上,所有
2016/12/18
岭回归的作用也是为了消除变量间的相关性的。
说一下步骤:
1.先对数据进行长度单位化(即均值为0,长度为1)
2.构造新的变量,如:
3.对新的变量做普通最小二乘,画出岭迹图,确定k(0<k<1)。
4.系数转化
例子:
下面为这次例子的数据
{{149.3, 4.2, 108.1, 15.9}, {161.2, 4.1, 114.8, 16.4}, {171.5, 3.1,
123.2, 19.}, {175.5, 3.1, 126.9, 19.1}, {180.8, 1.1, 132.1,
18.8}, {190.7, 2.2, 137.7, 20.4}, {202.1, 2.1, 146., 22.7}, {212.4,
5.6, 154.1, 26.5}, {226.1, 5., 162.3, 28.1}, {231.9, 5.1, 164.3,
27.6}, {239., 0.7, 167.6, 26.3}}1.对数据长度单位化
datastd = Transpose[data];
datastd = datastd[[#]] - Mean[datastd[[#]]] & /@ {1, 2, 3, 4};
datastd = Normalize[datastd[[#]]] & /@ {1, 2, 3, 4};
datastd = Transpose[datastd]2.构造新的变量
aa = DiagonalMatrix[Table[Sqrt[k], 3]]; bb = Map[Append[#, 0] &, aa, 1]; cc = Join[datastd, bb]; cc // TableForm
3.画出岭迹图,确定k
xishu = LinearModelFit[cc /. {k -> #}, {x1, x2, x3}, {x1, x2, x3},
IncludeConstantBasis -> False]["BestFitParameters"] & /@
Table[i, {i, 0, 1, 0.01}];
ListPlot[Transpose[xishu], PlotRange -> All, ImageSize -> Large,
PlotLegends -> Automatic]可以看到大概在第四点后开始平稳,即k=0.04
4.计算原系数
xishu = LinearModelFit[cc /. {k -> 0.04}, {x1, x2, x3}, {x1, x2, x3},
IncludeConstantBasis -> False]["BestFitParameters"];
{b1, b2, b3} = (StandardDeviation[data[[All, -1]]]/
StandardDeviation[data[[All, #]]])*xishu[[#]] & /@ {1, 2, 3}
Mean[data[[All, -1]]] - b1*Mean[data[[All, 1]]] -
b2*Mean[data[[All, 2]]] - b3*Mean[data[[All, 3]]]以上,所有
2016/12/18


