[回归分析][15]--总结

[回归分析][15]--总结

 
  马上也要到2017了，回归这个系列就不拖到明年了，今天把这篇总结的写完，也就差不多了。

  这个总结我是想把这一系列里常用的函数归纳一下，一些是自带的，一些是我自己写的，放在一起，也方便以后查找吧。

lm = LinearModelFit[datan, x, x]
(*画散点图和拟合图*)
Show[ListPlot[datan, ImageSize -> Medium], 
 Plot[lm[x], {x, 0, 270}, ImageSize -> Medium]]
(*画残差图*)
cancha = lm["FitResiduals"];
ListPlot[cancha, PlotRange -> All]
(*方差分析表格*)
lm["ANOVATable"]
(*系数表格*)
lm["ParameterTable"]
(*R^2*)
Grid[
{{"R^2", "调整的R^2"},lm[{ "RSquared", "AdjustedRSquared"}]}, 
Frame -> All, Spacings -> {1, 1}]

上面是模型的总体情况的评价

(*检验正太性--pp图*)
ProbabilityPlot[cancha]
(*计算D-W统计量(DW统计量用于看残差是否有范式)--见回归分析[10] *)
lm["DurbinWatsonD"]
(*计算游程数--看残差是否有范式--见回归分析[10]*)
cancha = lm["FitResiduals"];
RunLength[cancha_List] := Block[{n1, n2, u, v2, youcheng, ycn},
  n1 = Length[Select[cancha, # >= 0 &]];
  n2 =  Length[Select[cancha, # < 0 &]];
  u = (2.*n1*n2/(n1 + n2)) + 1;
  v2 = (2.*n1*n2*(2*n1*n2 - n1 - n2))/((n1 + n2)^2*(n1 + n2 - 1));
  youcheng = {};
  For[i = 1, i <= Length[cancha], i++,
   If[cancha[[i]] >= 0, youcheng = AppendTo[youcheng, 1], 
     youcheng = AppendTo[youcheng, -1]];
   ];
  ycn = 0;
  For[i = 1, i <= Length[youcheng] - 1, i++,
   If[youcheng[[i + 1]] - youcheng[[i]] != 0, ycn = ycn + 1];
   ];
  Grid[{{"期望", " | ", "方差", " | ", "游程数"}, {u, " | ", v2, " | ", 
     ycn}}, Frame -> True]
  ]

上面是残差部分的

(*相关系数矩阵--见回归分析[11]*)
mat = Correlation[data] // MatrixForm
(*画出两两的图像*)
Grid[
 Table[ListPlot[data[[All, {1, 2, 3, 4, 5}]][[All, {i, j}]],
   PlotStyle -> Directive[PointSize[Medium]],
         FrameTicks -> None, 
   Frame -> True, 
   Axes -> None,
   PlotLabel -> 
    Row[{"\[Rho] : ", 
      Correlation[data[[All, {1, 2, 3, 4, 5}]]][[i, j]]}]], {i, 1, 
   5}, {j, 1, 5}],
 Spacings -> {1, 1}
 ]
(*VIF--越小越说明线性相关--见回归分析[11]*)
Grid[{bl[[{1, 2, 3, 4, 5, 6}]], lm["VarianceInflationFactors"]}, 
 Frame -> All]
(*计算相关系数矩阵的特征值*)
lm["EigenstructureTable"]
(*变换的式子*)
mat = Correlation[data[[All, {2, 3, 4, 5, 6}]]];
vet = Eigenvectors[mat];
Column["c" <> ToString[#] <> " == " <> 
    ToString[
     TraditionalForm[Apply[Plus, vet[[#]]*{x1, x2, x3, x4, x5}]]] & /@
   Range[5], Spacings -> 1.5, Frame -> All]

上面是看系数的相关性的
主成分分析的话看我写的就可以了，链接如下
主成分分析

(*保留变量*)
datastd = Transpose[data];
length = Length[datastd];
datastd = datastd[[#]] - N[Mean[datastd[[#]]]] & /@ Range[length];
datastd = Normalize[datastd[[#]]] & /@ Range[length];
datastd = Transpose[datastd];
aa = DiagonalMatrix[Table[Sqrt[k], length - 1]];
bb = Map[Append[#, 0] &, aa, 1];
cc = Join[datastd, bb];
canshu = {{x1}, {x1, x2}, {x1, x2, x3}};
(*这里参数的个数要与题目要求的相等*)
finddel = {x1, x2, x3};
pic = Table[0, length - 2];
delcanshu = Table[0, length - 2];
nowcanshu = Table[0, length - 2];
Do[
  xishu = 
   LinearModelFit[cc /. {k -> #}, canshu[[-j]], canshu[[-j]], 
       IncludeConstantBasis -> False]["BestFitParameters"] & /@ 
    Table[i, {i, 0, 1, 0.01}];
  xishu = Transpose[xishu];
  pic[[j]] = 
   ListPlot[xishu, PlotRange -> All, PlotLegends -> Automatic, 
    PlotMarkers -> Automatic, ImageSize -> Large];
  (*找到系数最小的值--绝对值最小*)
  abs = Abs[xishu[[All, -1]]];
  Print[abs];
  min = Min[abs];
  pos = Position[abs, min];
  pos = pos[[1]];
  (*查看去掉的是哪个参数*)
  nowcanshu[[j]] = finddel;
  delcanshu[[j]] = finddel[[pos]];
  finddel = Delete[finddel, pos];
  (*去掉数据后重新拟合*)
  datastd = Transpose[Delete[Transpose[datastd], pos]];
  aa = DiagonalMatrix[Table[Sqrt[k], length - 1 - j]];
  bb = Map[Append[#, 0] &, aa, 1];
  cc = Join[datastd, bb];
  , {j, 1, length - 2}];
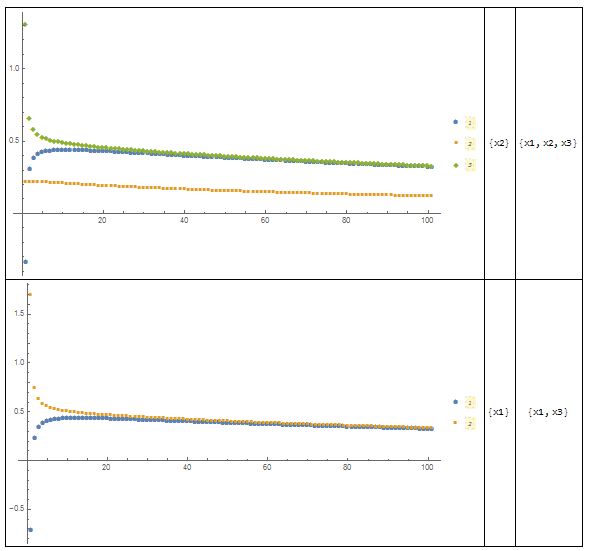
Grid[Transpose[{pic, delcanshu, nowcanshu}], Frame -> All]

上面是岭回归用来筛选变量的代码，看一下最后的效果

解释一下，三列依次为 岭迹图，删除的变量，留下的变量上面就大概把所有用到的总结了一下，
也是希望查的时候更加方便一点

以上，所有
2016/12/28