[机器学习][1]--PLA算法
[机器学习][1]--PLA算法
PLA全称为,Perception Learning Algorithm,中文叫感知学习算法。今天我会简单介绍一下这个算法,并用mathematica来实现一下这个算法。
放两个链接,里面的文章讲的不错的。
PLA算法总结与证明
感知器算法PLA
我自己概括一下这个算法。可以结合下面的例子看。
首先,wi和threshold是要来求的,h(x)为分类用得函数,xi为以知的数据集
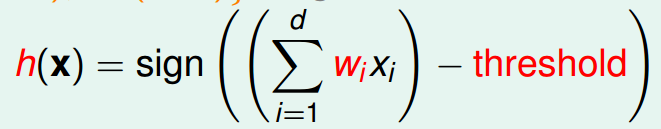
化简上面的式子,本来连加是从1开始的,现在把threshold放进去,下标从0开始

接下来我们的任务就是要确定w了。我们对每个数据集考虑,若带入上式时,不满足,则有下面两种情况。


若y=1时,h(x)=-1,则此时w = w+yx
若y=-1时,h(x)=1,则此时w = w+yx
因为权重后可能会导致前面的点出故障,需要从头再判断
这样把所有数据都考虑进去后,就能生成一个h(x)用来判断了。
下面我们来看一个例子
我们要预测一个人对于一个电影的喜欢程度,即对于某个固定的人来说,一部新上映的电影她是否喜欢。
数据集合(一个人以往看电影的数据):
data = {
{1, 3, -1}, {3, 4, 1},
{1, 2, -1}, {4, 2, 1},
{2, 2, -1}, {3, 5, 1},
{3, 1, -1}, {2.5, 4, 1},
{4, 0.5, -1}, {1, 6, 1},
{2.5, 1.5, -1}, {5, 1, 1},
{2, 1, -1}, {6, 2, 1},
{3, 1.5, -1}, {6, 0, 1},
{0, 4, -1}, {3, 3, 1}
};
其中各个位置的解释
{x1, x2, label} -> {动作片 (数字大小表示符合程度), 大片 (数字大小表示符合程度),喜欢 (1)/不喜欢 (-1)}, 表示一个人对不同电影的喜欢程度
首先,我们将data存在两个向量里。把电影类型和是否喜欢分开存

接着把x第一位都加上一个1,因为有w0

接着就可以进行迭代了
w = {0, 0, 0};
j = 1;
While[i <= Length[x],
If[
Sign[w.x[[i]]] != y[[i]],
w = w + y[[i]]*x[[i]]; i = 1,
i++
];
Print[w];
j++;
]
Print[j];
里面的j是用来看迭代次数的
 上面的格式有点问题,我截一张图。
上面的格式有点问题,我截一张图。

结果的部分图,可以看到最后w={-26,4.5,4.5},也就是说,当下一次输入为x1=1,x2=1时,则
{-26,4.5,4.5}.{1,1,1}=-1,所以不喜欢该电影。
上面为了得到式子一共迭代了347次(还是迭代了很多次的)
因为是二维的,所以可以在图上画出来

那条蓝色的线是{-26,4.5,4.5}.{1,x,y}=0,也就是x+y=26/4.5
在蓝色线上面的部分是1,下面是-1
画图部分的代码
temp = data[[All, {1, 2}]];
p1 = ListPlot[
Table[Style[temp[[i]], Hue[.25*data[[i, 3]] + .75]], {i, 1,
Length[data]}],
AxesOrigin -> {0, 0}];
p2 = Plot[-x + (26/4.5), {x, 0, 6.5}];
Show[p1, p2]
上面就大概把PLA算法讲完了。该算法只能用来解线性的。
下面链接是自己做的一个小作品,是用来看汉字结构的,把汉字的结构具体展现出来了,希望大家可以看看多提提意见。
汉字结构
以上,所有
2017/2/8
PLA全称为,Perception Learning Algorithm,中文叫感知学习算法。今天我会简单介绍一下这个算法,并用mathematica来实现一下这个算法。
放两个链接,里面的文章讲的不错的。
PLA算法总结与证明
感知器算法PLA
我自己概括一下这个算法。可以结合下面的例子看。
首先,wi和threshold是要来求的,h(x)为分类用得函数,xi为以知的数据集
化简上面的式子,本来连加是从1开始的,现在把threshold放进去,下标从0开始
接下来我们的任务就是要确定w了。我们对每个数据集考虑,若带入上式时,不满足,则有下面两种情况。
若y=1时,h(x)=-1,则此时w = w+yx
若y=-1时,h(x)=1,则此时w = w+yx
因为权重后可能会导致前面的点出故障,需要从头再判断
这样把所有数据都考虑进去后,就能生成一个h(x)用来判断了。
下面我们来看一个例子
我们要预测一个人对于一个电影的喜欢程度,即对于某个固定的人来说,一部新上映的电影她是否喜欢。
数据集合(一个人以往看电影的数据):
data = {
{1, 3, -1}, {3, 4, 1},
{1, 2, -1}, {4, 2, 1},
{2, 2, -1}, {3, 5, 1},
{3, 1, -1}, {2.5, 4, 1},
{4, 0.5, -1}, {1, 6, 1},
{2.5, 1.5, -1}, {5, 1, 1},
{2, 1, -1}, {6, 2, 1},
{3, 1.5, -1}, {6, 0, 1},
{0, 4, -1}, {3, 3, 1}
};
其中各个位置的解释
{x1, x2, label} -> {动作片 (数字大小表示符合程度), 大片 (数字大小表示符合程度),喜欢 (1)/不喜欢 (-1)}, 表示一个人对不同电影的喜欢程度
首先,我们将data存在两个向量里。把电影类型和是否喜欢分开存
x = data[[All, {1, 2}]];
y = data[[All, 3]];接着把x第一位都加上一个1,因为有w0
接着就可以进行迭代了
w = {0, 0, 0};
j = 1;
While[i <= Length[x],
If[
Sign[w.x[[i]]] != y[[i]],
w = w + y[[i]]*x[[i]]; i = 1,
i++
];
Print[w];
j++;
]
Print[j];
里面的j是用来看迭代次数的
结果的部分图,可以看到最后w={-26,4.5,4.5},也就是说,当下一次输入为x1=1,x2=1时,则
{-26,4.5,4.5}.{1,1,1}=-1,所以不喜欢该电影。
上面为了得到式子一共迭代了347次(还是迭代了很多次的)
因为是二维的,所以可以在图上画出来
那条蓝色的线是{-26,4.5,4.5}.{1,x,y}=0,也就是x+y=26/4.5
在蓝色线上面的部分是1,下面是-1
画图部分的代码
temp = data[[All, {1, 2}]];
p1 = ListPlot[
Table[Style[temp[[i]], Hue[.25*data[[i, 3]] + .75]], {i, 1,
Length[data]}],
AxesOrigin -> {0, 0}];
p2 = Plot[-x + (26/4.5), {x, 0, 6.5}];
Show[p1, p2]
上面就大概把PLA算法讲完了。该算法只能用来解线性的。
下面链接是自己做的一个小作品,是用来看汉字结构的,把汉字的结构具体展现出来了,希望大家可以看看多提提意见。
汉字结构
以上,所有
2017/2/8


