关于ArcTan的一个公式--ArcTan(a)+ArcTan(b)
关于ArcTan的一个公式--ArcTan(a)+ArcTan(b)
今天在查ArcTan的公式ArcTan(a)+ArcTan(b)的时候,发现现在网上能查到的都是错的。先看一下百度百科和互动百科写的。


可以看到是一样的,都是arctanA+arctanB = arctan[(A+B)/(1-AB)]
我们来看一下这个公式当A=2,B=3的时候就是不对的

我们可以看到当a=2,b=3时,两者的差是Pi,很显然是不对的。
那么公式究竟应该是什么呢,我们首先去看一下原来那个公式是怎么推导出来的。
在网山找到了推到的过程(我改动了一下,原版有错误):
后来发现问题就出在下面这一步上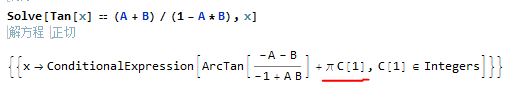
我们可以看到进行arctan运算,后面要加上k*Pi,这就是为什么我们上面结果多了Pi的原因。
其实推导也就是最后一步要改正一下,改完后如下:
最后我们来看一下为什么进行arctan运算要加上k*Pi

我们可以看到其实arctan(-1)既可以是-45度也可以是135度,要看a,b这两个角度来看是否要加上Pi,若两者和在二三象限,既要加Pi,否则不要加。
其实我们也可以得到在一四象限的两个角的Tan相成,乘积不大于1。
我已经去百度百科那里编辑了。
以上,所有
2017/3/8
我们来看一下这个公式当A=2,B=3的时候就是不对的
我们可以看到当a=2,b=3时,两者的差是Pi,很显然是不对的。
那么公式究竟应该是什么呢,我们首先去看一下原来那个公式是怎么推导出来的。
在网山找到了推到的过程(我改动了一下,原版有错误):
令a=arctanA,b=arctanB tan(a+b)=(tana+tanb)/(1-tana×tanb)=(A+B)/(1-AB) 所以 arctanA+arctanB =a+b =arctan(tan(a+b)) =arctan[(A+B)/(1-AB)]乍一看好像没什么错误,都很对。我也是一开始觉得没什么问题。
后来发现问题就出在下面这一步上
arctan(tan(a+b))=arctan[(A+B)/(1-AB)]我们可以看到进行arctan运算,后面要加上k*Pi,这就是为什么我们上面结果多了Pi的原因。
其实推导也就是最后一步要改正一下,改完后如下:
令a=arctanA,b=arctanB tan(a+b)=(tana+tanb)/(1-tana×tanb)=(A+B)/(1-AB) 所以 arctanA+arctanB =a+b =arctan(tan(a+b)) =arctan[(A+B)/(1-AB)]+k*Pi //其中k为0或1改动都在最后一句。
最后我们来看一下为什么进行arctan运算要加上k*Pi
我们可以看到其实arctan(-1)既可以是-45度也可以是135度,要看a,b这两个角度来看是否要加上Pi,若两者和在二三象限,既要加Pi,否则不要加。
其实我们也可以得到在一四象限的两个角的Tan相成,乘积不大于1。
我已经去百度百科那里编辑了。
以上,所有
2017/3/8





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具