洛谷P10693

洛谷P10693

好奇怪的题目编号

题面

\(n\)个人，\(2n\)个座位，每个人都有心仪的座位，如\(i\)心仪的座位为\(a_i\)（可重复），设计师设计让他们坐在自己编号的位置上，即\(i\)做到\(i\)，每个人只可以做\(a_i\)或\(i\)，最多多少个人坐到心仪的座位。

思路提取

input
11
2 13 4 5 3 7 9 9 11 11 12
output
9

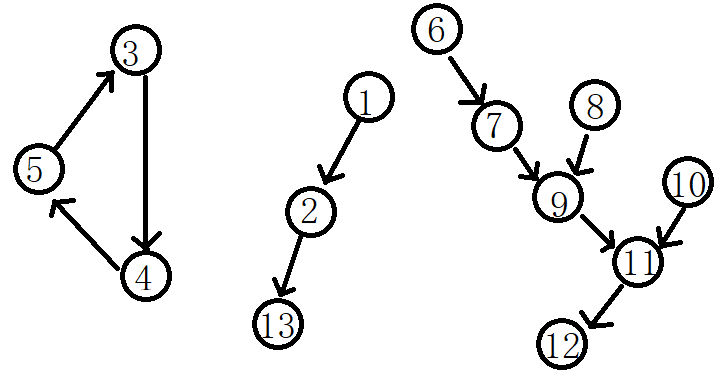
以人造数据为例。
首先我们让\(i\)\(\to\)\(a_i\)连边，整个分三种情况（对应图中三部分）。

• 第一部分：\(i\)坐到了\(a_i\)（\(a_i\)\(\le\)\(n\)）这个位置，那么\(a_i\)就没有地方坐了，他只能坐到他心仪的位置，也就是\(a_{a_i}\)（\(a_{a_i}\)\(\le\)\(n\)），以此类推，如果最后一个人\(k\)心仪的位置是\(i\)，也就是\(a_k=i,\)也就是他坐回了\(i\)这个位置，也就是他又连向了\(i\)，也就是形成了一个环，那么环上的所有人都可以做到心仪的位置上去，且最终把环上所有人原来的位置（即设计师设计的位置）都占满了，不会影响到环外的人，所有环都是如此，环的大小均可加入答案中。

• 第二部分：注意到第一部分有两个细节\(a_i\)\(\le\)\(n\)和\(a_{a_i}\)\(\le\)\(n\)，那么如果大于了呢？那就连不下去了，就会出现链的情况，链中的所有人也都可以坐到心仪的位置，链的长度也都可加入。

• 第三部分：前两部分其实都有一个潜在的前提，就是所有人心仪的位置都不重复，那如果重复了呢？就会变成第三部分——有向树，其中这个“向”都是冲着根节点的。因为每个人只有一个心仪的位置，所以出度只能为\(1\)，如果不是统一方向，就会有点出度为\(2\)不符合要求，而如果都冲子节点，根节点就有可能不符合要求。第三部分就注定有人坐不到心仪的位置，那么要取最大的，想到第二部分，我们发现最大的其实就是最长链，因为一条链上的点一定是可以都满足的（让他们顺着坐即可，最后一定是连到了\(>n\)的位置才停的）。可以发现第二部分其实是第三部分的特殊情况。

代码思路

先考虑最后两部分（也可以说是一个部分），可以用一个\(DFS\)来解决，从\(>n\)的位置，也就是停止的位置开始往回搜，建反边，搜一个最大深度即可，那么没搜到的就是环了。
是吗？

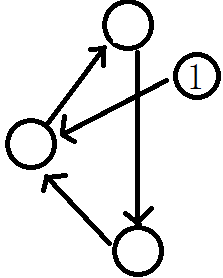
如果是这样呢？多出的\(1\)号点并不会在上述的\(DFS\)中被搜到，但它又确确实实不可以满足，所以我们还需要一个拓扑排序，把剩下的连在环上的多余部分标记了，剩下的没标记的就是环了。这里标记多余部分并不会标记多了（把环的一部分也标记了），因为环终究没有入度为\(0\)的，不会进入拓扑序。
注意：环要用正边。

代码

#include<bits/stdc++.h>

using namespace std;

int n;
int a[200005];
vector<int> ed[200005],ned[200005];
int ind[200005];
int da;
int ans;
bool vs[200005];

void dfs(int x,int dp){
		vs[x] = 1;
		da = max(da,dp);
	for(int i = 0;i < ed[x].size();++ i){
		int y = ed[x][i];
		dfs(y,dp+1);
	}
}

signed main(){
	
	cin >> n;
	for(int i = 1;i <= n;++ i){
		cin >> a[i];
		ed[a[i]].push_back(i);
		ned[i].push_back(a[i]); 
		ind[a[i]]++;
	}
	
	for(int i = n+1;i <= n*2;++ i){
		da = 0,dfs(i,0),ans += da; 
	} 
	
	queue<int> q;
	for(int i = 1;i <= n;++ i){
		if((!ind[i])&&(!vs[i])) q.push(i);
	}
	while(!q.empty()){
		int t = q.front();q.pop();
		vs[t] = 1;
		for(int i = 0;i < ned[t].size();++ i){
			if((--ind[ned[t][i]]) == 0) q.push(ned[t][i]);
		}
	}
	
	for(int i = 1;i <= n;++ i)
		if(!vs[i]) ans++;
	cout << ans;
	
	return 0;
	
} 

完结撒花！