20182322 2019-2020-1 《数据结构与面向对象程序设计》实验9报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 王美皓
学号:20182322
实验教师:王志强
实验日期:2019年11月25日
必修/选修: 必修
1.实验内容
完成图的综合实践
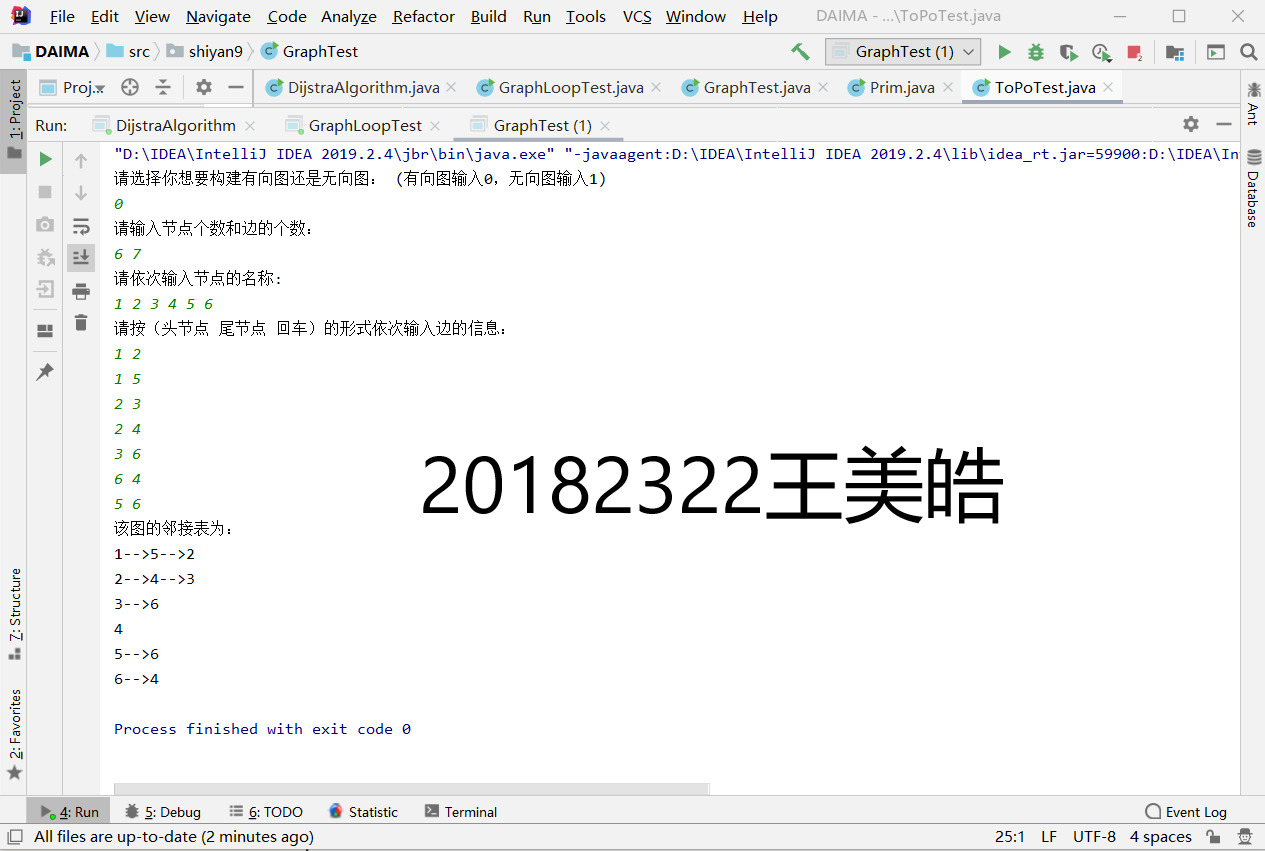
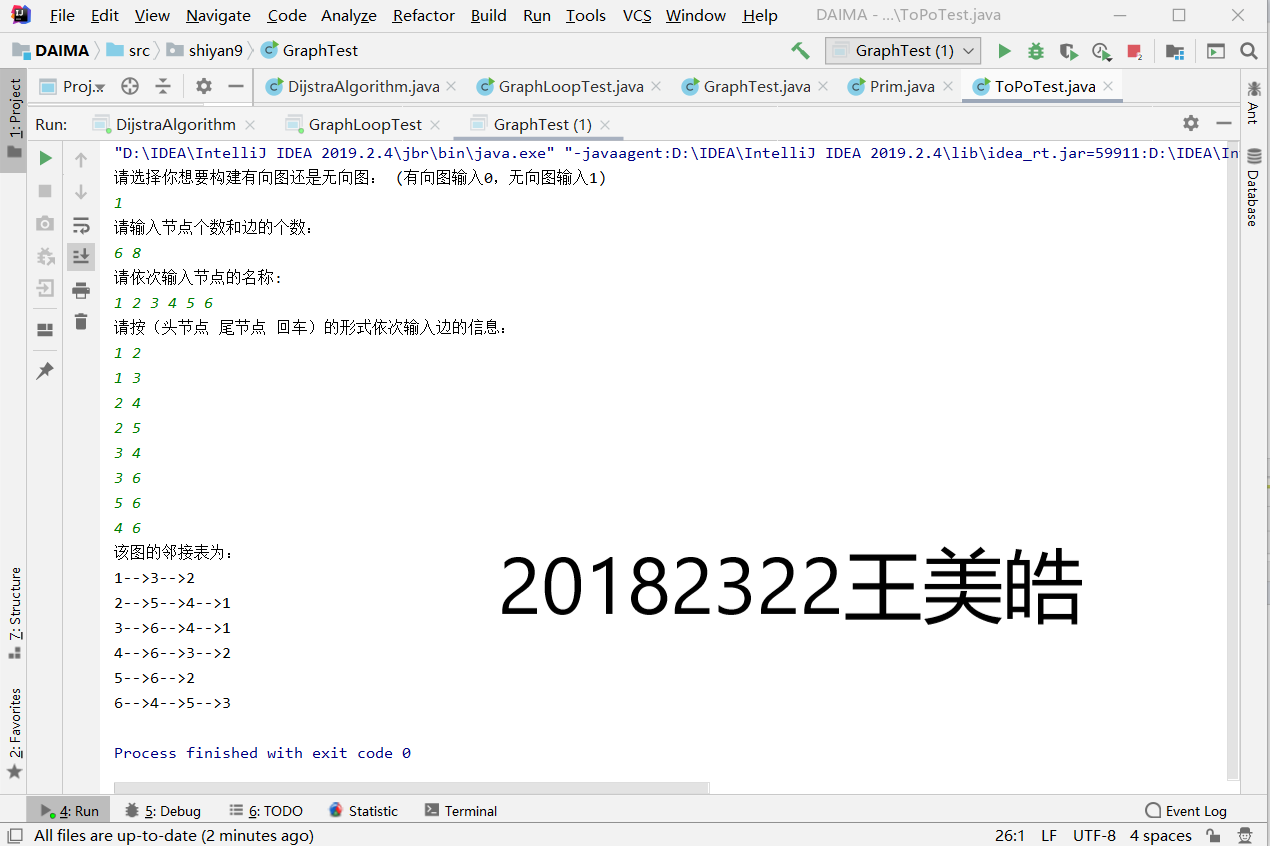
(1)初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
(2)图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
(3)完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环
(4)完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出
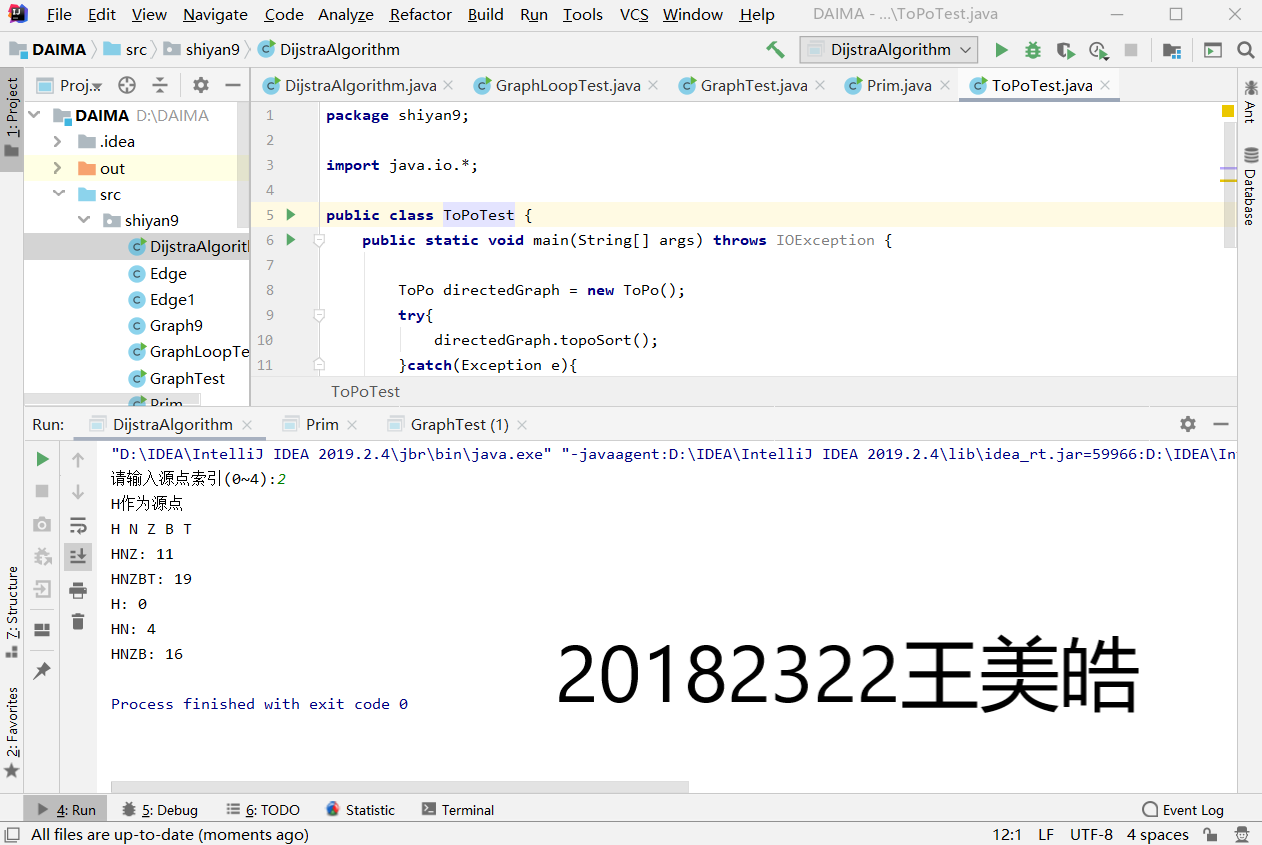
(5)完成有向图的单源最短路径求解(迪杰斯特拉算法)
2. 实验过程及结果
- 实验一创建图,初始化无向图和有向图
//设置边及它的权值
private class B {
int i,w;//设置权值
B nextX; //设置指针
}
//设置顶点
private class N {
char dingdian; // 设置顶点
B firstX;
};
private int Enum; // 边的数量
private N[] mV; // 顶点数组
//创建图
public Sorting(char[] dingdian, EData[] bian) {
int lenv = dingdian.length;
int elen = bian.length;
// 初始化顶点
mV= new N[lenv];
for (int i = 0; i < mV.length; i++) {
mV[i] = new N();
mV[i].dingdian = dingdian[i];
mV[i].firstX = null;
}
// 初始化边
Enum = elen;
for (int i = 0; i < elen; i++) {
// 读取顶点
char c1 = bian[i].start;
char c2 = bian[i].end;
int weight = bian[i].weight;
int p1 = gPs(c1);
int p2 = gPs(c2);
B node1 = new B ();
node1.i = p2;
node1.w = weight;
//连接
if(mV[p1].firstX == null)
mV[p1].firstX = node1;
else
Connect(mV[p1].firstX, node1);
B node2 = new B ();
node2.i = p1;
node2.w = weight;
//连接
if(mV[p2].firstX == null)
mV[p2].firstX = node2;
else
Connect(mV[p2].firstX, node2);
}
}
private void Connect(B list, B node) {
B p = list;
while(p.nextX!=null)
p = p.nextX;
p.nextX = node;
}
private int gPs(char ch) {
for(int i=0; i<mV.length; i++)
if(mV[i].dingdian==ch)
return i;
return -1;
}
-
-
-
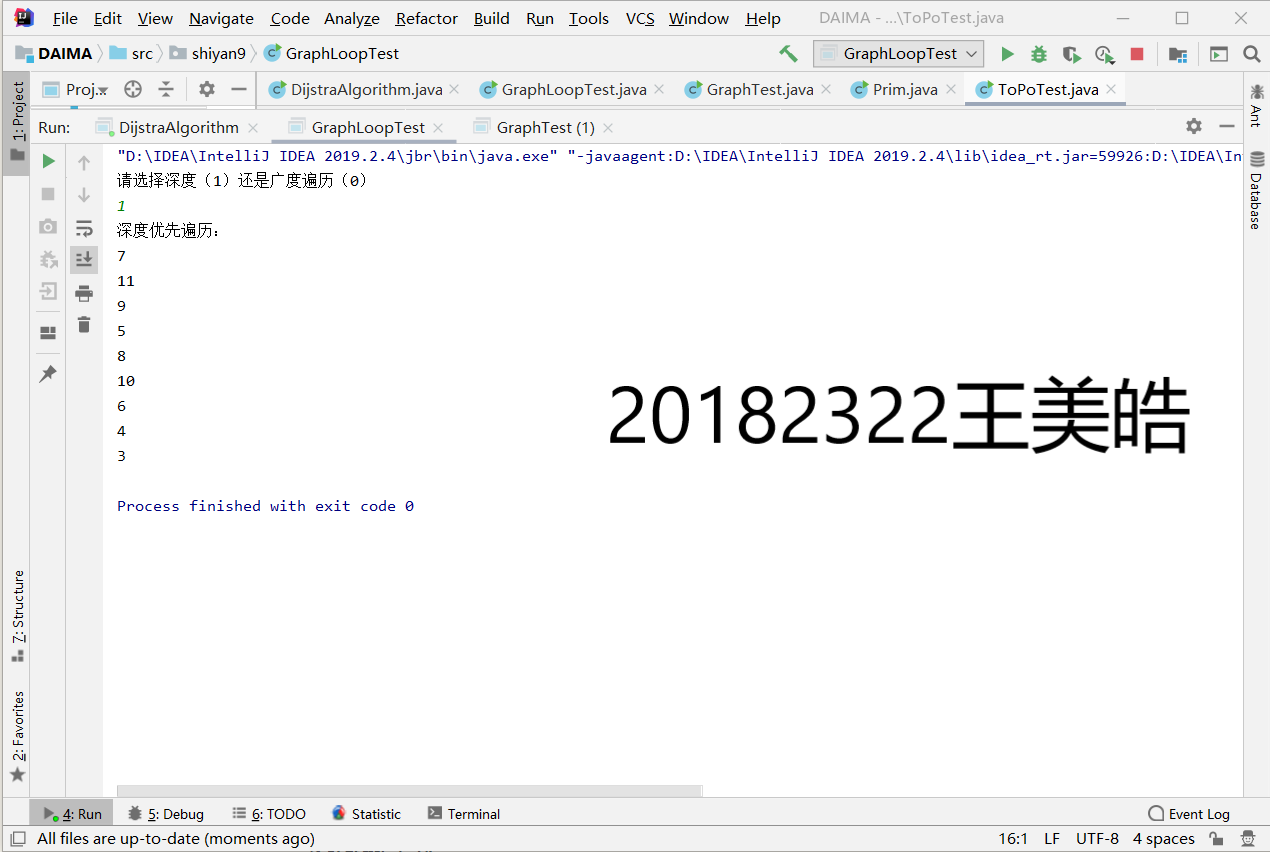
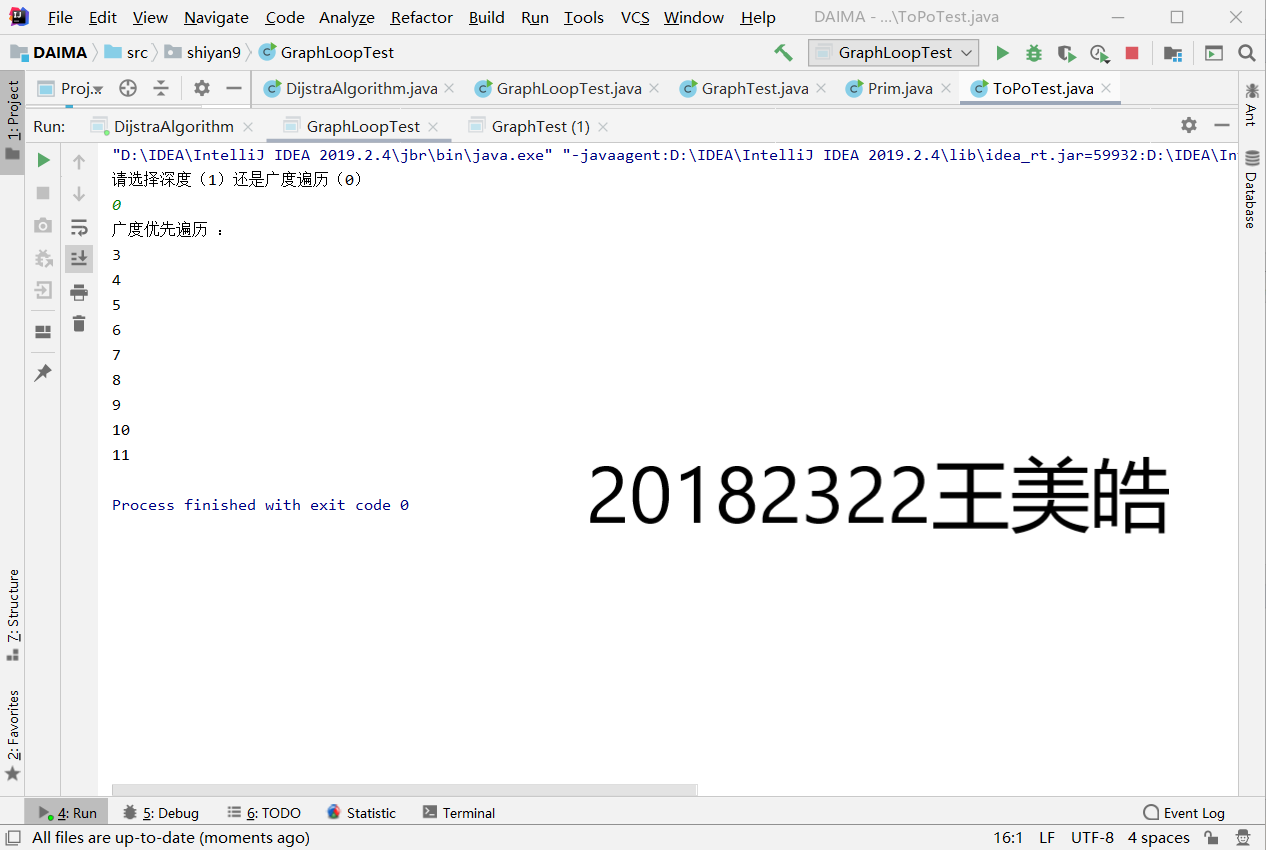
实验二完成图的遍历
private void DFS(int i, boolean[] BL) {
B node;
BL[i] = true;
System.out.printf("%c ", mV[i].dingdian);
node = mV[i].firstX;
while (node != null) {
if (!BL[node.i])
DFS(node.i, BL);
node = node.nextX;
}
}
public void DFS() {
boolean[] BL = new boolean[mV.length];
for (int i = 0; i < mV.length; i++)
BL[i] = false;
for (int i = 0; i < mV.length; i++) {
if (!BL[i])
DFS(i, BL);
}
System.out.printf("\n");
}
/*
广度优先
*/
public void BFS() {
int head = 0;
int rear = 0;
int[] queue = new int[mV.length]; // 辅组队列
boolean[] BL = new boolean[mV.length]; // 顶点访问标记
for (int i = 0; i < mV.length; i++)
BL[i] = false;
for (int i = 0; i < mV.length; i++) {
if (!BL[i]) {
BL[i] = true;
System.out.printf("%c ", mV[i].dingdian);
queue[rear++] = i; // 入队列
}
while (head != rear) {
int j = queue[head++]; // 出队列
B node = mV[j].firstX;
while (node != null) {
int k = node.i;
if (!BL[k])
{
BL[k] = true;
System.out.printf("%c ", mV[k].dingdian);
queue[rear++] = k;
}
node = node.nextX;
}
}
}
System.out.printf("\n");
}
-
-
-
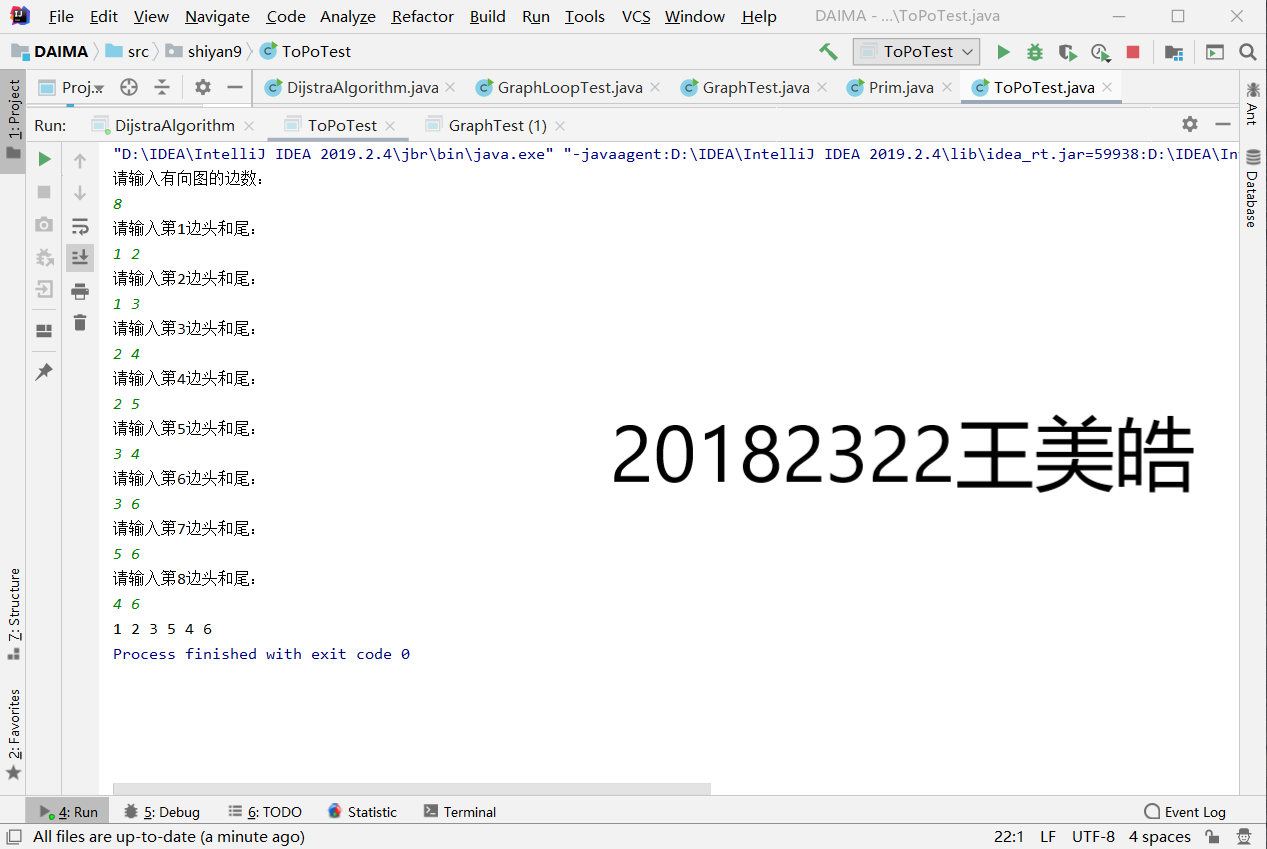
实验3完成拓扑排序
public int TpSort() {
int index = 0;
int num = mV.length;
int[] ins; // 入度数组
char[] tops;
Queue<Integer> queue;
ins = new int[num];
tops = new char[num];
queue = new LinkedList<Integer>();
// 统计每个顶点的入度数
for(int i = 0; i < num; i++) {
B node = mV[i].firstX;
while (node != null) {
ins[node.i]++;
node = node.nextX;
}
}
// 将所有入度为0的顶点入队列
for(int i = 0; i < num; i ++)
if(ins[i] == 0)
queue.offer(i); // 入队列
while (!queue.isEmpty()) { // 队列非空
int j = queue.poll().intValue(); // 出队列。j是顶点的序号
tops[index++] = mV[j].dingdian;
B node = mV[j].firstX;
while(node != null) {
// 入度减1。
ins[node.i]--;
// 若入度为0,则入队列
if( ins[node.i] == 0)
queue.offer(node.i); // 入队列
node = node.nextX;
}
}
if(index != num) {
System.out.printf("有向有环图\n");
return 1;
}
// 打印拓扑排序结果
System.out.printf("拓扑排序: ");
for(int i = 0; i < num; i ++)
System.out.printf("%c ", tops[i]);
System.out.printf("\n");
return 0;
}
-
-
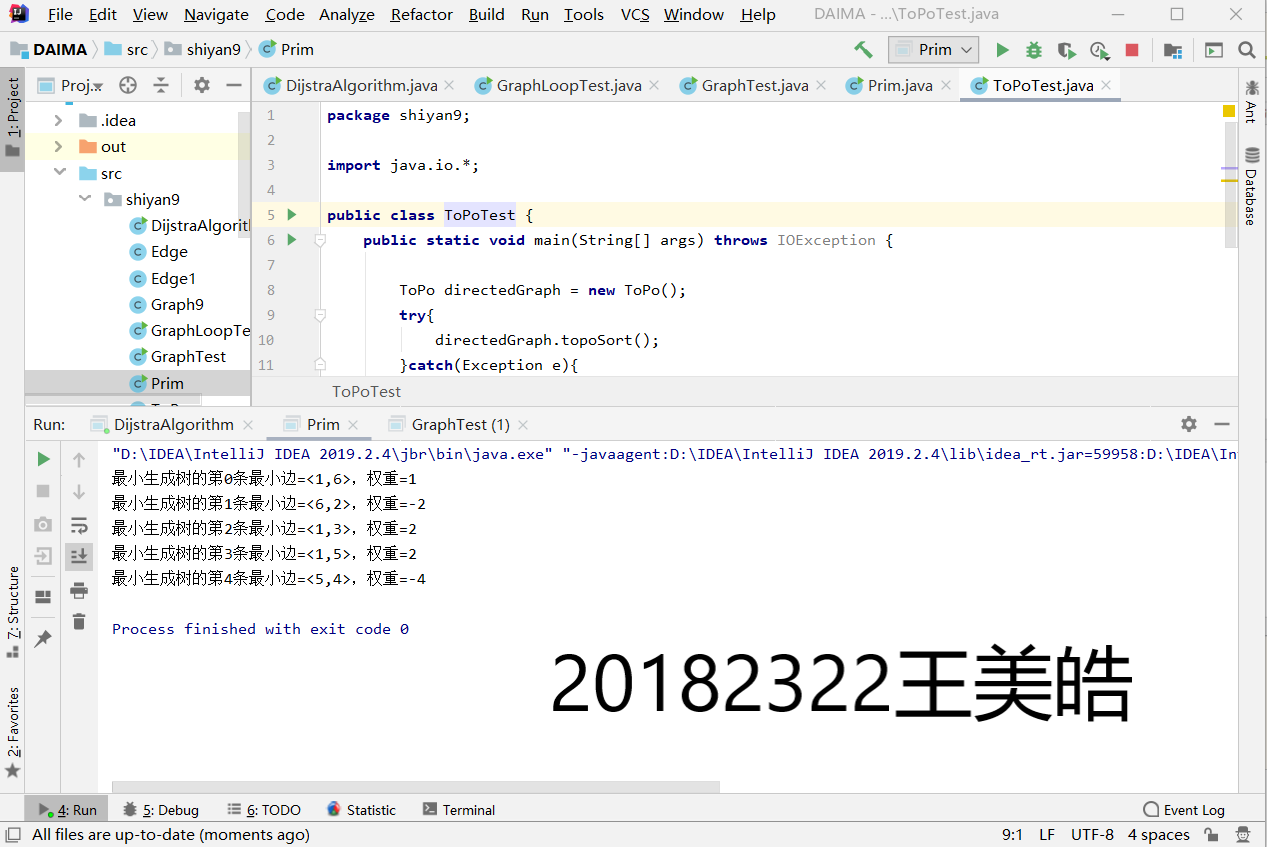
实验4用Kruscal算法完成最小生成树
//完成无向图的最小生成树Kruscal算法并输出
//获得权重
private int getWeight(int start, int end) {
if (start==end)
return 0;
B node = mV[start].firstX;
while (node!=null) {
if (end==node.i)
return node.w;
node = node.nextX;
}
return INF;
}
public void kruskal() {
int index = 0;
int[] v = new int[Enum]; // 保存终点。
EData[] rets = new EData[Enum]; // 暂存结果数组
EData[] e; // 对应的所有边
e = getEdges();
// 将边按权排序
sortEdges(e, Enum);
for (int i=0; i<Enum; i++) {
int p1 = gPs(e[i].start);
int p2 = gPs(e[i].end);
int m = getEnd(v, p1);
int n = getEnd(v, p2);
// 如果m!=n,则没有形成环路
if (m != n) {
v[m] = n;
rets[index++] = e[i];
}
}
// print
int length = 0;
for (int i = 0; i < index; i++)
length += rets[i].weight;
System.out.printf("Kruskal=%d: ", length);
for (int i = 0; i < index; i++)
System.out.printf("(%c,%c) ", rets[i].start, rets[i].end);
System.out.printf("\n");
}
private EData[] getEdges() {
int index=0;
EData[] edges;
edges = new EData[Enum];
for (int i=0; i < mV.length; i++) {
B node = mV[i].firstX;
while (node != null) {
if (node.i > i) {
edges[index++] = new EData(mV[i].dingdian, mV[node.i].dingdian, node.w);
}
node = node.nextX;
}
}
return edges;
}
private void sortEdges(EData[] edges, int elen) {
for (int i=0; i<elen; i++) {
for (int j=i+1; j<elen; j++) {
if (edges[i].weight > edges[j].weight) {
// 交换"边i"和"边j"
EData tmp = edges[i];
edges[i] = edges[j];
edges[j] = tmp;
}
}
}
}
/*
* 获取i的终点
*/
private int getEnd(int[] vends, int i) {
while (vends[i] != 0)
i = vends[i];
return i;
}
-
-
实验五用迪杰斯特拉算法算出最短路径
public void dijkstra(int s, int[] q, int[] t) {
// flag[i]=true表示最短路径已成功获取。
boolean[] flag = new boolean[mV.length];
// 初始化
for (int i = 0; i < mV.length; i++) {
flag[i] = false;
q[i] = 0; // 顶点i的前驱顶点为0。
t[i] = getWeight(s, i);
}
// 初始化
flag[s] = true;
t[s] = 0;
int k = 0;
for (int i = 1; i < mV.length; i++) {
// 寻找当前最小的路径;
// 寻找当前最小的路径;
// 寻找当前最小的路径;
int min = INF;
for (int j = 0; j < mV.length; j++) {
if (flag[j]==false && t[j]<min) {
min = t[j];
k = j;
}
}
// 获取到最短路径
flag[k] = true;
for (int j = 0; j < mV.length; j++) {
int tmp = getWeight(k, j);
tmp = (tmp==INF ? INF : (min + tmp)); // 防止溢出
if (flag[j]==false && (tmp<t[j]) )
{
t[j] = tmp;
q[j] = k;
}
}
}
//print
System.out.printf("dijkstra(%c): \n", mV[s].dingdian);
for (int i = 0; i < mV.length; i++)
System.out.printf(" (%c, %c)=%d\n", mV[s].dingdian, mV[i].dingdian, t[i]);
}
// 边的结构体
private static class EData {
char start; // 边的起点
char end; // 边的终点
int weight; // 边的权重
public EData(char start, char end, int weight) {
this.start = start;
this.end = end;
this.weight = weight;
}
};
3. 实验过程中遇到的问题和解决过程
- 问题一:各种空指针报错
- 问题一解决方法:重新编辑驱动代码,确认调用无误值已初始化。
- 问题二:输出图的列表时,不能进行排列
- 问题二解决方法:修改数组定义的问题
其他(感悟、思考等)
- 图这一内容学离散懂了一些,理论知识我还是很容易理解,但代码方面对我来说还有一定困难,还需要多加练习。