哈夫曼编码实践

课程：《程序设计与数据结构》

班级： 1823

姓名： 王美皓

学号：20182322

实验教师：王志强

实验日期：2019年11月15日

必修/选修： 必修

1.实验内容

设有字符集：S={a,b,c,d,e，f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。

给定一个包含26个英文字母的文件，统计每个字符出现的概率，根据计算的概率构造一颗哈夫曼树。并完成对英文文件的编码和解码。

要求：
准备一个包含26个英文字母的英文文件（可以不包含标点符号等），统计各个字符的概率

构造哈夫曼树

对英文文件进行编码，输出一个编码后的文件

对编码文件进行解码，输出一个解码后的文件

撰写博客记录实验的设计和实现过程，并将源代码传到码云

把实验结果截图上传到云班课

2. 实验过程及结果

哈夫曼树

1. 节点之间的路径长度：在树中从一个结点到另一个结点所经历的分支，构成了这两个结点间的路径上的经过的分支数称为它的路径长度
2. 树的路径长度：从树的根节点到树中每一结点的路径长度之和。在结点数目相同的二叉树中，完全二叉树的路径长度最短。
3. 结点的权：在一些应用中，赋予树中结点的一个有某种意义的实数。
4. 结点的带权路径长度：结点到树根之间的路径长度与该结点上权的乘积
5. 树的带权路径长度：定义为树中所有叶子结点的带权路径长度之和
6. 最优二叉树：从已给出的目标带权结点(单独的结点) 经过一种方式的组合形成一棵树.使树的权值最小.。最优二叉树是带权路径长度最短的二叉树。根据结点的个数，权值的不同，最优二叉树的形状也各不相同。它们的共同点是：带权值的结点都是叶子结点。权值越小的结点，其到根结点的路径越长。

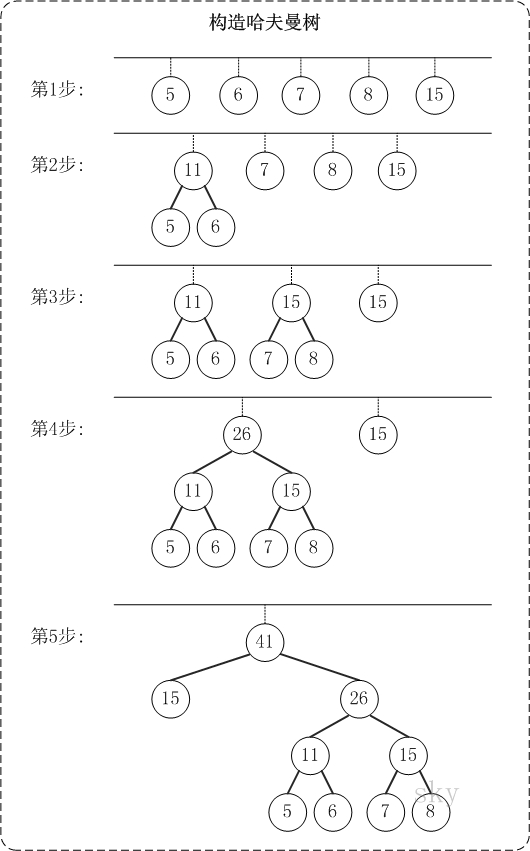
哈夫曼编码步骤

1、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算法，一般还要求以Ti的权值Wi的升序排列。）

2、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。

3、从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。

4、重复二和三两步，直到集合F中只有一棵二叉树为止。

• 

• 实验截图

• 

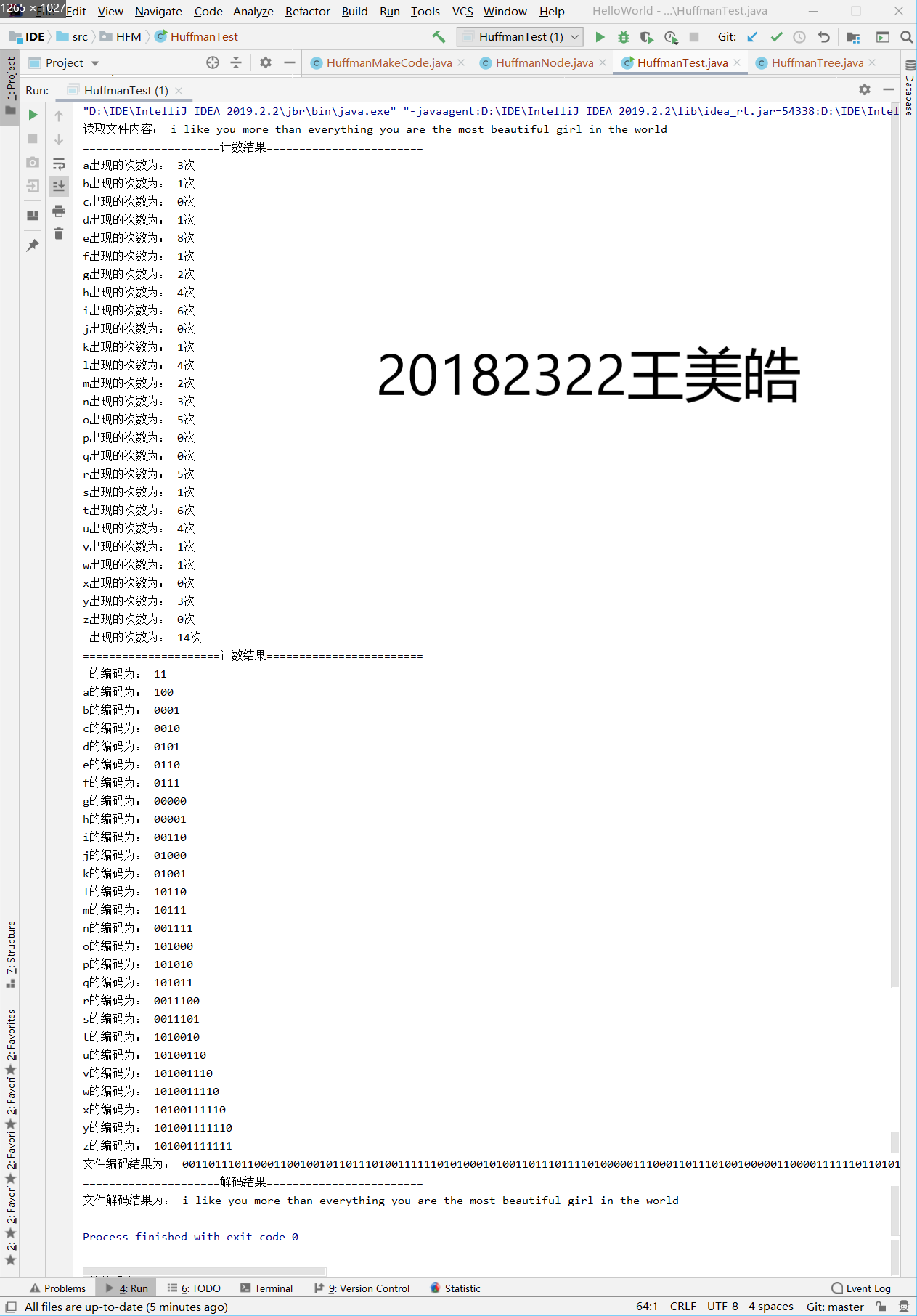
其他（感悟、思考等）

• 哈夫曼树的编码解码也比较有意思，编码的思路自己一开始理清了，解码其实就是一个逆过程，但自己没有想到，直到参看资料才有了思路。
• 由于临近期末，事情比较多，实验的时间并没有合理安排，学习哈夫曼树并不是十分的充分。以后应该合理规划时间和学习进度。