17.程序员常用的10种算法
1.二分查找算法(非递归)
/**
* 二分查找算法:非递归
*/
public class BinarySearchNoRecur {
public static void main(String[] args) {
int arr[] = {1, 3, 8, 10, 11, 67, 100};
System.out.println(1 + "的index=" + binarySearch(arr, 1));
System.out.println(8 + "的index=" + binarySearch(arr, 8));
System.out.println(11 + "的index=" + binarySearch(arr, 11));
}
/**
* 非递归二分查找算法
*
* @param arr 查找数组
* @param target 查找目标
* @return 目标下标
*/
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
//这里是关键
while (left <= right) {
int mid = (left + right) / 2;
if (target == arr[mid]) {
return mid;
} else if (target > arr[mid]) {
//目标大于中间值
left = mid + 1;
} else {
//目标小于中间值
right = mid - 1;
}
}
return -1;
}
}
测试输出:
1的index=0
8的index=2
11的index=42.分治算法


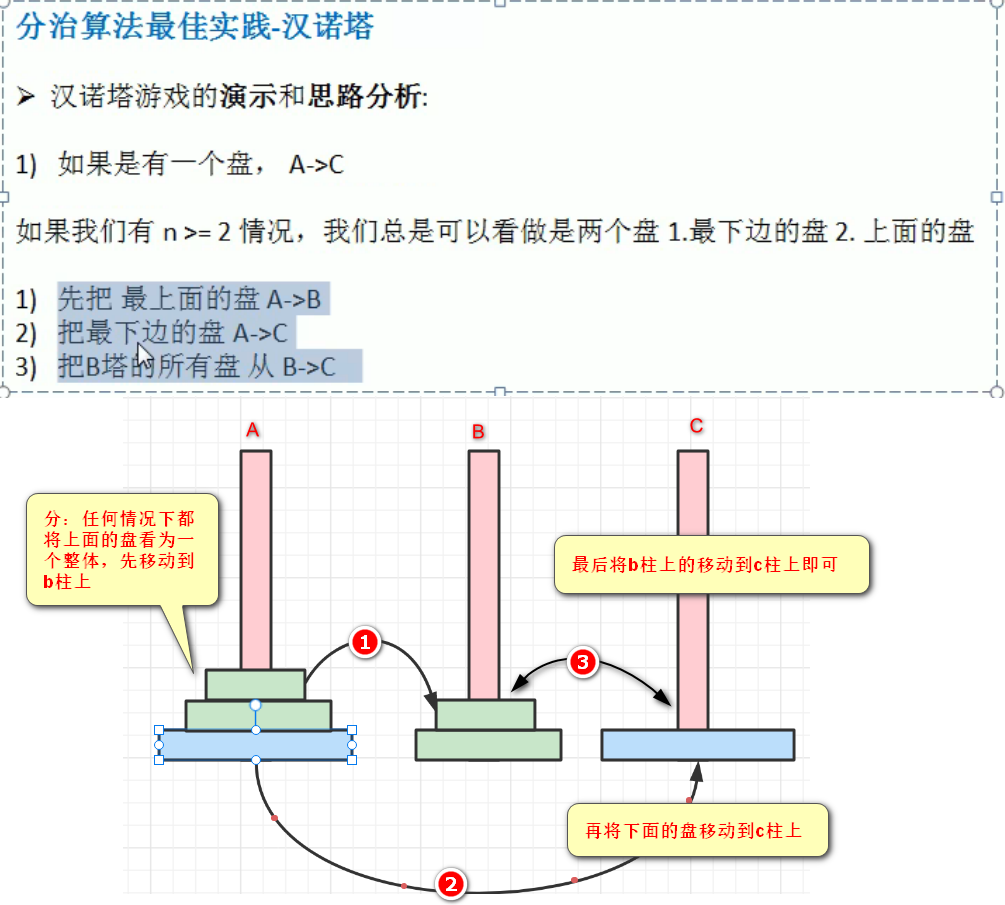
分治算法实现汉诺塔

/**
* 分治算法实现汉诺塔
*/
public class Hanoitower {
private static int count=0;
public static void main(String[] args) {
hanoiTower(5,'a','b','c');
System.out.println("5盘总共移动:"+count);
}
/**
* @param num 有多少个盘
* @param a a柱
* @param b b柱
* @param c c柱
*/
public static void hanoiTower(int num, char a, char b, char c) {
count++;
if (num == 1) {
//只有一个盘,直接a->c
System.out.println("第1个盘从 " + a + "->" + c);
} else {
/*
有多个盘,我们可以将整体看为两个盘
1.最下面的一个盘
2.上面所有的盘
*/
//1.先将上面的盘全部移动到B柱, A->B,移动的过程中会使用到C
hanoiTower(num - 1, a, c, b);
//2.把最下面的盘移动到C柱
System.out.println("第"+num+"个盘从 "+a+"->"+c);
//3.将b柱的所有盘移动到c,移动的过程中用到a
hanoiTower(num-1,b,a,c);
}
}
}/**
* 分治算法实现汉诺塔
*/
public class Hanoitower {
private static int count=0;
public static void main(String[] args) {
hanoiTower(5,'a','b','c');
System.out.println("5盘总共移动:"+count);
}
/**
* @param num 有多少个盘
* @param a a柱
* @param b b柱
* @param c c柱
*/
public static void hanoiTower(int num, char a, char b, char c) {
count++;
if (num == 1) {
//只有一个盘,直接a->c
System.out.println("第1个盘从 " + a + "->" + c);
} else {
/*
有多个盘,我们可以将整体看为两个盘
1.最下面的一个盘
2.上面所有的盘
*/
//1.先将上面的盘全部移动到B柱, A->B,移动的过程中会使用到C
hanoiTower(num - 1, a, c, b);
//2.把最下面的盘移动到C柱
System.out.println("第"+num+"个盘从 "+a+"->"+c);
//3.将b柱的所有盘移动到c,移动的过程中用到a
hanoiTower(num-1,b,a,c);
}
}
}
测试输出:5个盘总共移动了31次
第1个盘从 a->c
第2个盘从 a->b
第1个盘从 c->b
第3个盘从 a->c
第1个盘从 b->a
第2个盘从 b->c
第1个盘从 a->c
第4个盘从 a->b
第1个盘从 c->b
第2个盘从 c->a
第1个盘从 b->a
第3个盘从 c->b
第1个盘从 a->c
第2个盘从 a->b
第1个盘从 c->b
第5个盘从 a->c
第1个盘从 b->a
第2个盘从 b->c
第1个盘从 a->c
第3个盘从 b->a
第1个盘从 c->b
第2个盘从 c->a
第1个盘从 b->a
第4个盘从 b->c
第1个盘从 a->c
第2个盘从 a->b
第1个盘从 c->b
第3个盘从 a->c
第1个盘从 b->a
第2个盘从 b->c
第1个盘从 a->c
5盘总共移动:31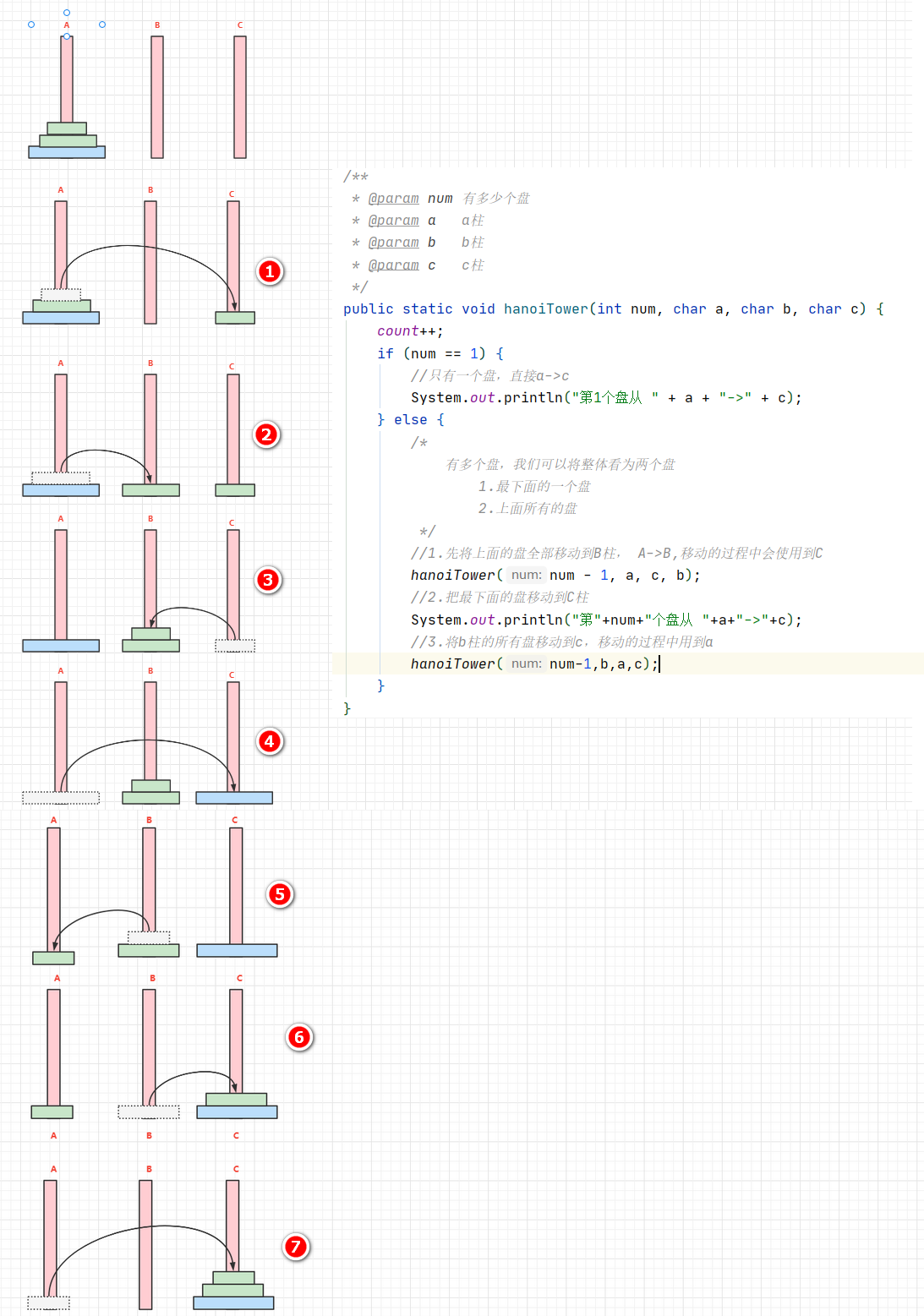
三个盘子的汉诺塔顺序
第1个盘从 a->c
第2个盘从 a->b
第1个盘从 c->b
第3个盘从 a->c
第1个盘从 b->a
第2个盘从 b->c
第1个盘从 a->c
3盘总共移动:73.动态规划算法(这个没听懂,暂放)
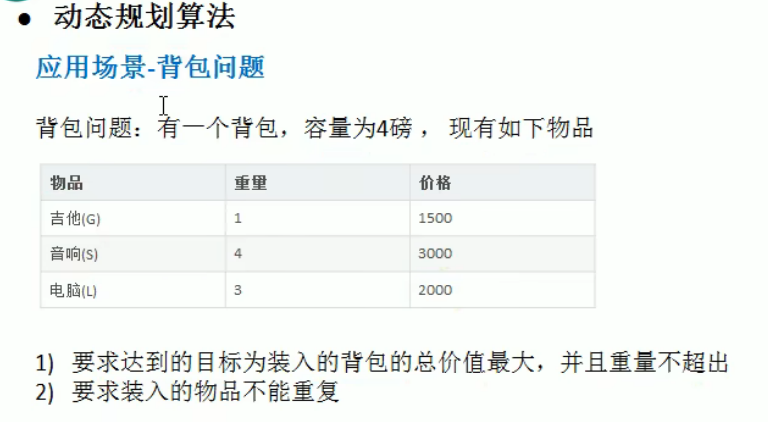


4.贪心算法




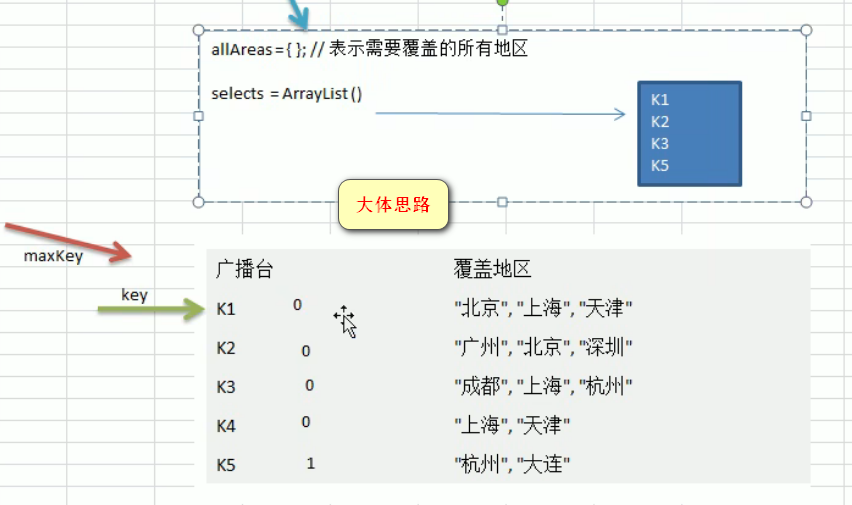
/**
* 贪心算法
*/
public class GreedyAlgorithm {
public static void main(String[] args) {
//key为电台名称 value为覆盖地区集合
Map<String, HashSet<String>> broadCasts = new HashMap<>();
HashSet<String> k1 = new HashSet<>();
k1.add("北京");
k1.add("上海");
k1.add("天津");
broadCasts.put("k1", k1);
HashSet<String> k2 = new HashSet<>();
k2.add("广州");
k2.add("北京");
k2.add("深圳");
broadCasts.put("k2", k2);
HashSet<String> k3 = new HashSet<>();
k3.add("成都");
k3.add("上海");
k3.add("杭州");
broadCasts.put("k3", k3);
HashSet<String> k4 = new HashSet<>();
k4.add("天津");
k4.add("上海");
broadCasts.put("k4", k4);
HashSet<String> k5 = new HashSet<>();
k5.add("杭州");
k5.add("大连");
broadCasts.put("k5", k5);
//存放所有的地区
HashSet<String> allAreas = new HashSet<>();
for (HashSet<String> area : broadCasts.values()) {
allAreas.addAll(area);
}
//创建list存放选择的电台集合
List<String> selects = new ArrayList<>();
//定义一个临时set,存放与所有地区地区的交集
HashSet<String> tempSet = new HashSet<>();
//定义一个maxKey指针,指向一次遍历中,与所有地区交集最大的广播
String maxKey = null;
//每次匹配后,会将匹配成功的地区从总集合中删除掉
while (allAreas.size() > 0) {
//因为下面代码可能会对其赋值,影响再次遍历
maxKey = null;
for (String key : broadCasts.keySet()) {
tempSet.clear();
HashSet<String> areas = broadCasts.get(key);
tempSet.addAll(areas);
//求出该广播对应的地区与总地区的交集,并赋值给tempset
tempSet.retainAll(allAreas);
if (tempSet.size() > 0
&& (maxKey == null || tempSet.size() > broadCasts.get(maxKey).size())) {
//这里的条件需要注意的是:找出与地区集合交集最大的广播
maxKey = key;
}
}
//经过上述循环,找到了交集最大的一个广播
if (maxKey != null) {
//将其放入到广播集合中
selects.add(maxKey);
//地区集合删除对应的地区
allAreas.removeAll(broadCasts.get(maxKey));
//map集合去掉该广播,以防遍历时再次遍历(节约时间而已,也可以不用去除)
//broadCasts.remove(maxKey);
}
}
System.out.println("最终的贪心广播集合:" + selects);
}
}
测试输出:
最终的贪心广播集合:[k1, k2, k3, k5]上述代码体现的贪心算法位置:
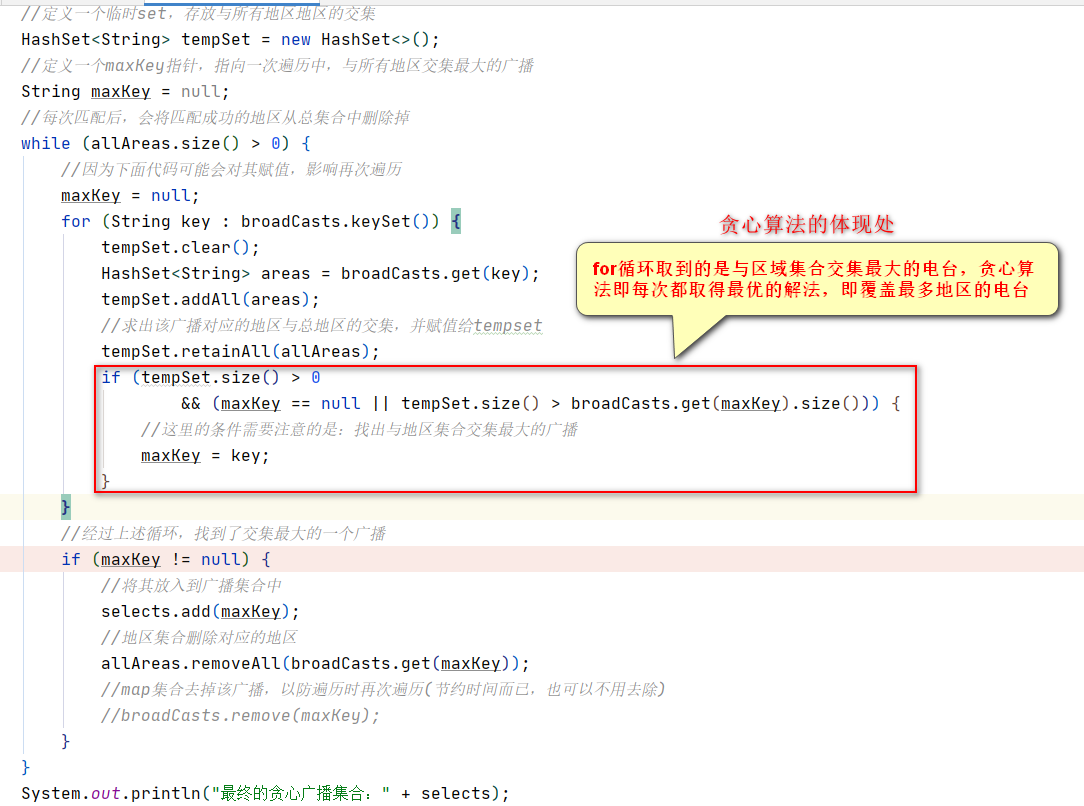
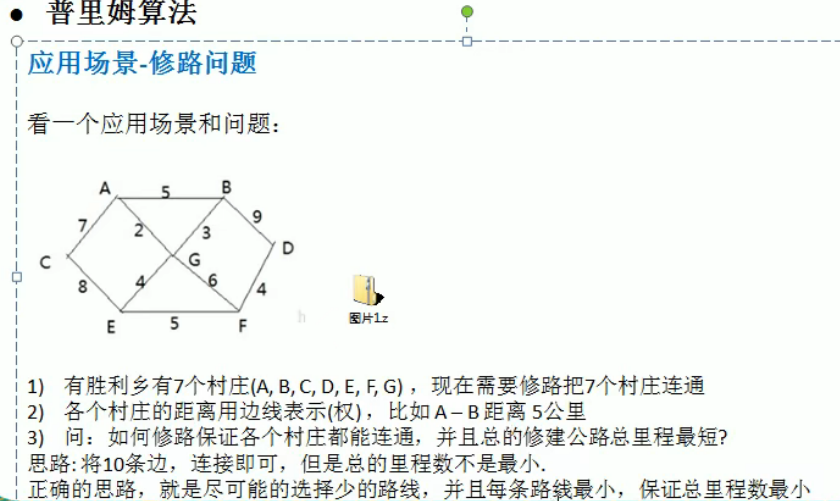
5.普利姆算法