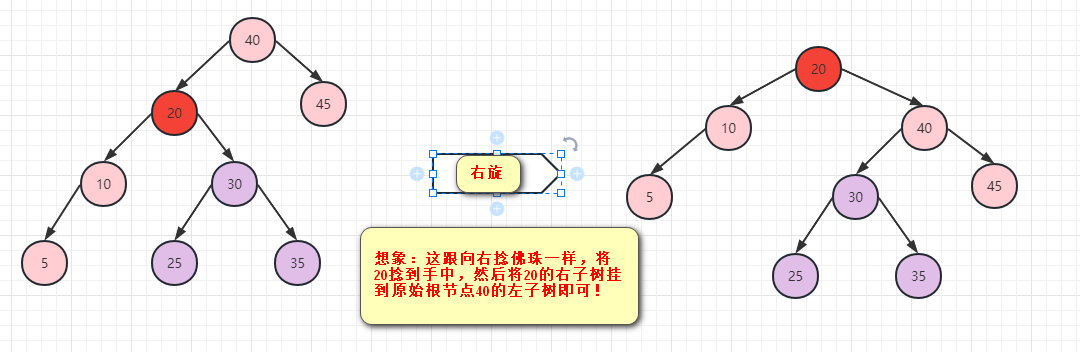
14.平衡二叉树（AVL树）
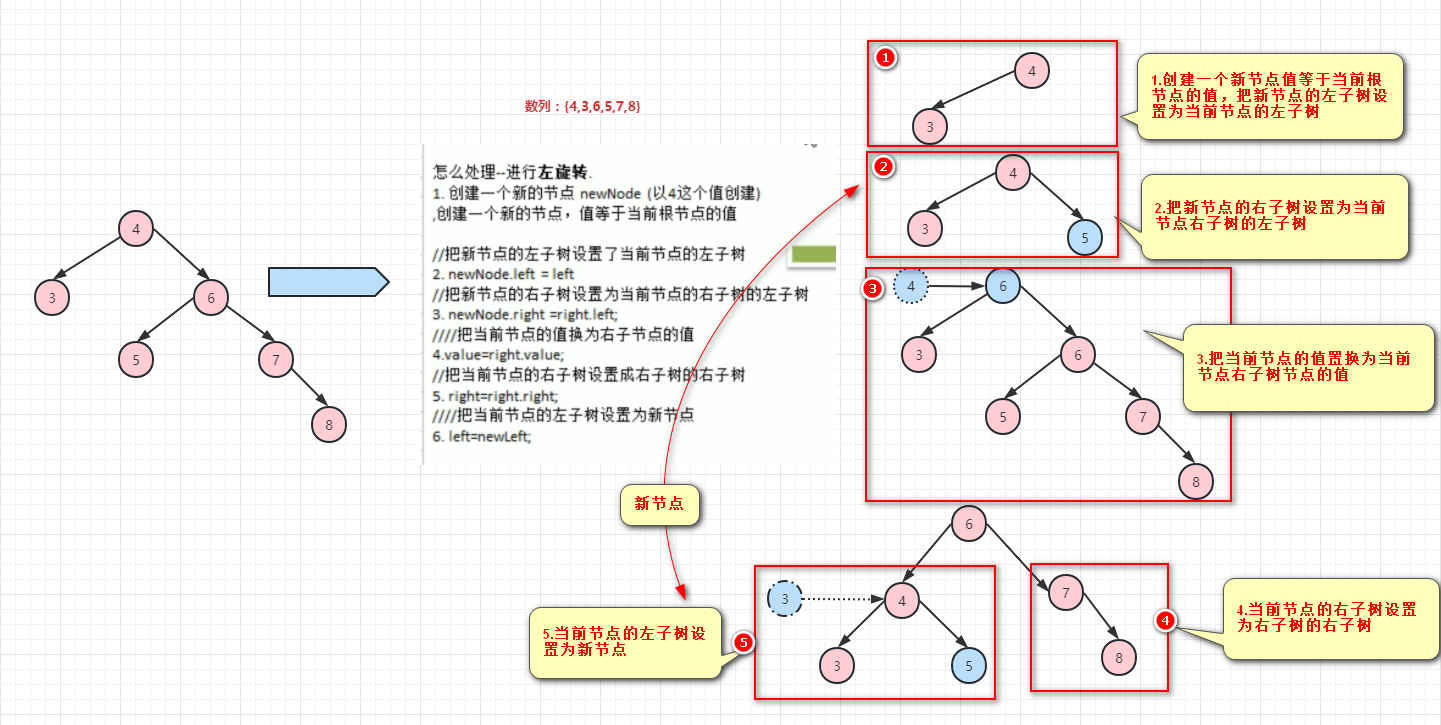
左旋转思想：当右子树的高度比左子树的高度高时(并且高度差绝对值超过了1时)
代码示例：
package cn.com.avlTree;
/**
* 平衡二叉树
*/
public class AvlTreeDemo {
public static void main(String[] args) {
int arr[] = {4, 3, 6, 5,7, 8};
AvlTree avlTree = new AvlTree();
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("中序遍历======");
avlTree.infixOrder();
System.out.println("\n节点4的高度：" + avlTree.height(4));
System.out.println("节点6的高度：" + avlTree.height(6));
System.out.println("节点3的高度：" + avlTree.height(3));
}
}
class AvlTree {
Node root;
/**
* 获取value节点为根节点的树的高度
*
* @param value 节点值
* @return 以value节点为根节点的数的高度
*/
public int height(int value) {
//查找到以value的节点
Node target = root.search(value);
int height=0;
if (target!=null){
height=target.height();
}
return height;
}
/**
* 添加元素
*
* @param node
*/
public void add(Node node) {
if (root == null) {
root = node;
} else {
this.root.add(node);
}
}
/**
* 中序遍历
*/
public void infixOrder() {
if (root == null) {
return;
}
this.root.infixOrder();
}
/**
* 1.返回以目标节点为根节点的二叉排序树的最小节点的值
* 2.删除目标节点为根节点的二叉排序树的最小节点
*
* @param node 目标节点的右子树节点
* @return 右子树的最小值
*/
public int delRightTreeMin(Node node) {
Node target = node;
//循环查找右子树中的左子树，找到的就是最小值
while (target.getLeft() != null) {
target = target.getLeft();
}
//删除最小节点
/*
思考点1：这里的代码为啥不直接写在删除代码中，而是抽取成一个方法呢
如果写在删除deleteNode方法中，那方法中就是递归调用，没有像方法返回一个唯一的值
回溯时可能会存在多次赋值的情况！
*/
deleteNode(target.getValue());
return target.getValue();
}
/**
* 删除节点
*
* @param value 删除的节点值
*/
public void deleteNode(int value) {
if (root == null) {
return;
}
//查找需要删除节点
Node target = root.search(value);
if (target == null) {
//没找到不处理
return;
}
//当只有一个节点并且就是需要删除的节点
if (root.getLeft() == null && root.getRight() == null) {
root = null;
}
//获取需要删除节点的父节点
Node parent = root.searchParent(value);
/*
*第一种情况：当需要删除的节点是叶子节点时
*/
if (target.getLeft() == null && target.getRight() == null) {
if (parent.getLeft() != null && parent.getLeft().getValue() == target.getValue()) {
//当需要删除的节点时父节点的左子节点时
parent.setLeft(null);
}
if (parent.getRight() != null && parent.getRight().getValue() == target.getValue()) {
parent.setRight(null);
}
} else if (target.getLeft() != null && target.getRight() != null) {
//目标节点的两个子节点都不为空,在右子树上找最小的值
int rightTreeMinValue = delRightTreeMin(target.getRight());
target.setValue(rightTreeMinValue);
} else {
//目标节点的一个节点为空
if (target.getLeft() != null) {
if (parent != null) {
//删除目标节点的左子节点不为空
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
//目标节点在父节点的左边
parent.setLeft(target.getLeft());
} else {
//目标节点在父节点的右边
parent.setRight(target.getLeft());
}
} else {
root = target.getLeft();
}
} else {
if (parent != null) {
//需要删除的节点有右子节点
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
parent.setLeft(target.getRight());
} else {
parent.setRight(target.getRight());
}
} else {
root = target.getRight();
}
}
}
}
}
class Node {
private int value;
//左节点
private Node left;
//右节点
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
/**
* 获取以当前节点为根节点的数的高度
*
* @return 以当前节点为根节点的数的高度
*/
public int height() {
return Math.max(left == null ? 0 : left.height(),
right == null ? 0 : right.height()) + 1;
}
/**
* 添加节点
*
* @param node 节点
*/
public void add(Node node) {
if (node == null) {
return;
}
//比当前节点小,放到左边
if (node.getValue() <= this.value) {
if (this.left != null) {
this.left.add(node);
} else {
this.left = node;
}
} else {
//比当前节点大，放在右边
if (this.right != null) {
this.right.add(node);
} else {
this.right = node;
}
}
}
/**
* 中序遍历
*/
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.print(this.value + " ");
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* 查找节点
*
* @param value 节点值
* @return 查找的节点
*/
public Node search(int value) {
if (this.value == value) {
return this;
}
//向左子树查找
if (value < this.value && this.left != null) {
return this.left.search(value);
} else if (value >= this.value && this.right != null) {
return this.right.search(value);
} else {
return null;
}
}
/**
* 查找节点的父节点
*
* @param value 查找的节点值
* @return 父节点
*/
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
}
//查找的值小于当前节点的值，向左查找
if (value < this.value && this.left != null) {
return this.left.searchParent(value);
} else if (value >= this.value && this.right != null) {
//大于当前节点的值，向右查找
return this.right.searchParent(value);
} else {
return null;
}
}
}
测试输出：
中序遍历======
3 4 5 6 7 8
节点4的高度：4
节点6的高度：3
节点3的高度：1
注意：平衡二叉树就是一种特殊的二叉排序树，只不过要求左右子树的高度差的绝对值不大于1
所以代码是在原始排序二叉树的基础上改造的，新增两个方法如下！
1.node节点中的获取节点高度
class Node {
private int value;
//左节点
private Node left;
//右节点
private Node right;
/**
* 获取以当前节点为根节点的数的高度
* 这里使用递归一层一层加上来的！
* @return 以当前节点为根节点的数的高度
*/
public int height() {
return Math.max(left == null ? 0 : left.height(),
right == null ? 0 : right.height()) + 1;
}
...
}
2.avltree代码
class AvlTree {
Node root;
/**
* 获取value节点为根节点的树的高度
*
* @param value 节点值
* @return 以value节点为根节点的数的高度
*/
public int height(int value) {
//查找到以value的节点
Node target = root.search(value);
int height=0;
if (target!=null){
height=target.height();
}
return height;
}
...
}左旋代码示例：
node节点代码：
class Node {
private int value;
//左节点
private Node left;
//右节点
private Node right;
/**
* 获取以当前节点为根节点的数的高度
*
* @return 以当前节点为根节点的数的高度
*/
public int height() {
return Math.max(left == null ? 0 : left.height(),
right == null ? 0 : right.height()) + 1;
}
/**
* 返回根节点的左子树的高度
*
* @return
*/
public int leftHeight() {
if (this.left == null) {
return 0;
}
return this.left.height();
}
/**
* 返回根节点的右子树的高度
*
* @return
*/
public int rightHeight() {
if (this.right == null) {
return 0;
}
return this.right.height();
}
/**
* 左旋转代码
*/
public void leftRoute() {
//1.创建一个新的节点，节点值为当前根节点的值，并把新节点的左子树设置为当前节点的左子树
//因为该刚发在avl数代码中用root节点调用的
Node newRoot = new Node(this.value);
newRoot.setLeft(this.left);
//2.把新节点的右子树设置为当前节点右子树的左子树
newRoot.setRight(this.right.left);
//3.把当前节点的值改为当前节点右子树的值
this.value = this.right.value;
//4.把当前节点的右子树设置为右子树的右子树
this.right = this.right.right;
//5.当前节点的左子树设置为新节点
this.left = newRoot;
}
/**
* 添加节点
*
* @param node 节点
*/
public void add(Node node) {
if (node == null) {
return;
}
//比当前节点小,放到左边
if (node.getValue() <= this.value) {
if (this.left != null) {
this.left.add(node);
} else {
this.left = node;
}
} else {
//比当前节点大，放在右边
if (this.right != null) {
this.right.add(node);
} else {
this.right = node;
}
}
//重点：添加节点的时候进行判断是否需要左旋
//如果右子树的高度-左子树高度 >1 时进行左旋
if ((this.rightHeight() - this.leftHeight()) > 1) {
leftRoute();
}
}
}
输出：
public static void main(String[] args) {
int arr[] = {4, 3, 6, 5,7, 8};
AvlTree avlTree = new AvlTree();
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("中序遍历======");
avlTree.infixOrder();
System.out.println();
System.out.println("节点6的高度：" + avlTree.height(6));
System.out.println("节点4的高度：" + avlTree.height(4));
System.out.println("节点7的高度：" + avlTree.height(7));
System.out.println("节点3的高度：" + avlTree.height(3));
}
输出：发现高度降低了
中序遍历======
3 4 5 6 7 8
节点6的高度：3
节点4的高度：2
节点7的高度：2
节点3的高度：1
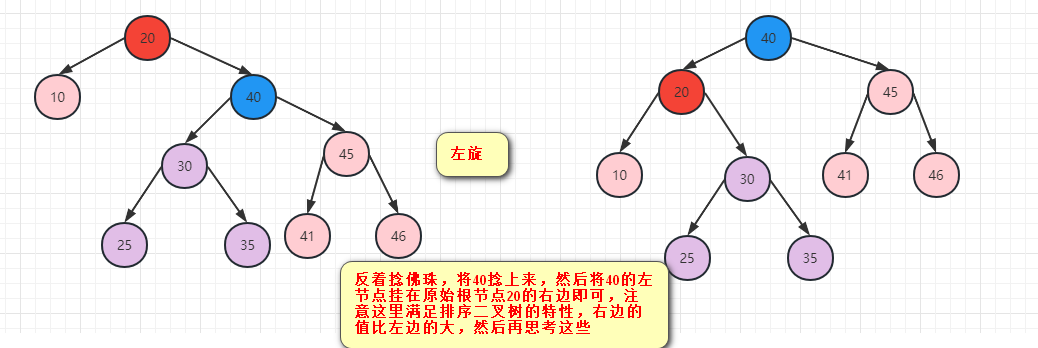
双旋转思想
有时候左旋和右旋不能解决二叉树高度问题，如下数列
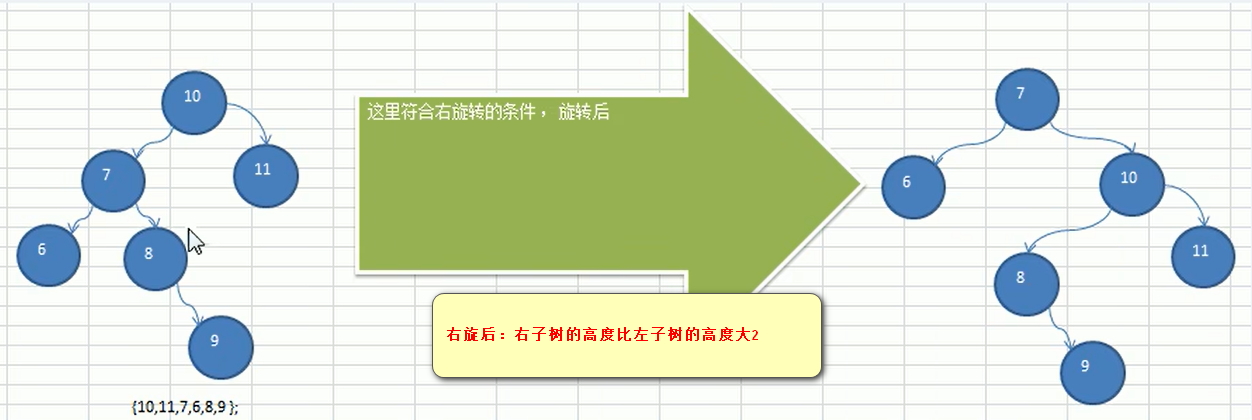
为什么会这样呢：
1.当复合右旋条件时，当左子树的右子树高度(8的高度为2)大于左子树的高度(6的高度为1)==>就会出现上述问题
解决办法
2.先对当前节点的左子树进行左旋转
3.再对当前节点的进行右旋转即可
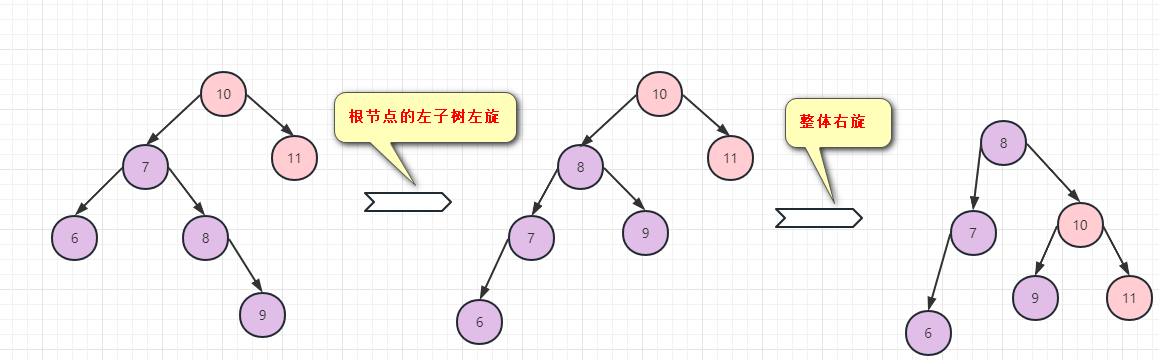
代码示例：需要在Node类中新增节点时进行判断，左右是对称的
/**
* 添加节点
*
* @param node 节点
*/
public void add(Node node) {
if (node == null) {
return;
}
//比当前节点小,放到左边
if (node.getValue() <= this.value) {
if (this.left != null) {
this.left.add(node);
} else {
this.left = node;
}
} else {
//比当前节点大，放在右边
if (this.right != null) {
this.right.add(node);
} else {
this.right = node;
}
}
//如果右子树的高度-左子树高度 >1 时进行左旋
if ((this.rightHeight() - this.leftHeight()) > 1) {
//当右子树的左子树高度>右子树右子树的高度时，先进行右子树右旋，在整体左旋
if (this.right != null && this.right.leftHeight() > this.right.rightHeight()) {
this.right.rightRoute();
this.leftRoute();
} else {
leftRoute();
}
return;
}
//如果左子树的高度-右子树高度 >1 时进行右旋
if (this.leftHeight() - this.rightHeight() > 1) {
//当根节点左子树的右子树高度大于根节点左子树的高度时，先对左子树进行左旋，在对整体进行右旋
if (this.left != null && this.left.rightHeight() > this.left.leftHeight()) {
this.left.leftRoute();
this.rightRoute();
} else {
//其他直接进行右旋
rightRoute();
}
}
}
测试：
public static void main(String[] args) {
int arr[] = {10, 11, 7, 6, 8, 9};
//int arr[] = {4,3,6,5,7,8};
AvlTree avlTree = new AvlTree();
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("中序遍历======");
avlTree.infixOrder();
System.out.println();
System.out.println("根节点：" + avlTree.root.getValue());
System.out.println("树的高度：" + avlTree.root.height());
System.out.println("左子树高度：" + avlTree.root.leftHeight());
System.out.println("右子树高度：" + avlTree.root.rightHeight());
}
输出：复合预期！
中序遍历======
6 7 8 9 10 11
根节点：8
树的高度：3
左子树高度：2
右子树高度：2总结：左旋右旋的思路
