13.二叉排序树
引入需求：
给定一个数列{7,3,10,12,5,1,9}要求能够高效的完成对数据的查询和添加
package cn.com.binarySortTree;
import java.util.Arrays;
/**
* 二叉排序树
* 对于任何一个非叶子节点，要求左节点的值比当前节点的值小，右子节点的值比当前节点的值大
*/
public class BinarySortTreeDemo {
public static void main(String[] args) {
int arr[] = {7, 3, 10, 12, 5, 1, 9};
System.out.println("原数组："+ Arrays.toString(arr));
BinarySortTree binarySortTree=new BinarySortTree();
for (int value : arr) {
binarySortTree.add(new Node(value));
}
System.out.println("前序遍历========");
binarySortTree.infixOrder();
}
}
/**
* 二叉树实体
*/
class BinarySortTree {
Node root;
/**
* 添加元素
*
* @param node
*/
public void add(Node node) {
if (root == null) {
root = node;
} else {
this.root.add(node);
}
}
/**
* 中序遍历
*/
public void infixOrder() {
if (root == null) {
return;
}
this.root.infixOrder();
}
}
class Node {
private int value;
//左节点
private Node left;
//右节点
private Node right;
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
/**
* 添加节点
*
* @param node 节点
*/
public void add(Node node) {
if (node == null) {
return;
}
//比当前节点小,放到左边
if (node.getValue() <= this.value) {
if (this.left != null) {
this.left.add(node);
} else {
this.left = node;
}
} else {
//比当前节点大，放在右边
if (this.right != null) {
this.right.add(node);
} else {
this.right = node;
}
}
}
/**
* 中序遍历
*/
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.print(this.value+" ");
if (this.right != null) {
this.right.infixOrder();
}
}
}
输出：
原数组：[7, 3, 10, 12, 5, 1, 9]
前序遍历========
1 3 5 7 9 10 12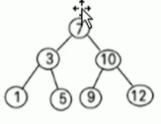 
符合中序遍历的结果！
二叉树的删除
思路分析
1.删除的节点是叶子节点
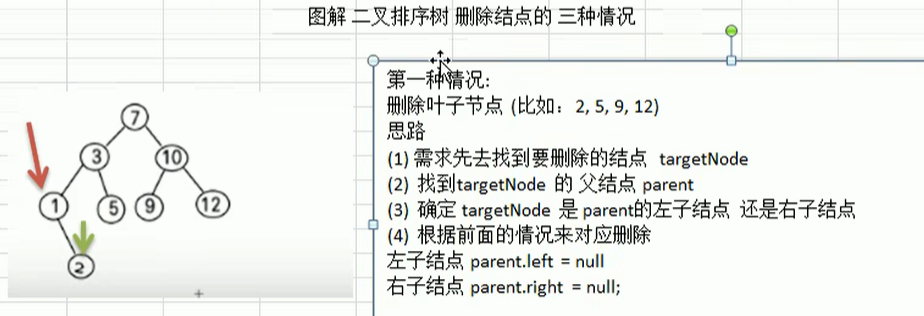
2.删除只有一个子树的节点
3.删除有两颗子树的节点（例如7,3,10 ）
3.1右子树只有一个节点
1.删除的是叶子节点
1.删除的节点是叶子节点
前提Node类新增两个方法
1.查找删除的节点
2.查找删除节点的父节点
class Node {
private int value;
//左节点
private Node left;
//右节点
private Node right;
/**
* 查找节点
*
* @param value 节点值
* @return 查找的节点
*/
public Node search(int value) {
if (this.value == value) {
return this;
}
//向左子树查找
if (value < this.value && this.left != null) {
return this.left.search(value);
} else if (value >= this.value && this.right != null) {
return this.right.search(value);
} else {
return null;
}
}
/**
* 查找节点的父节点
*
* @param value 查找的节点值
* @return 父节点
*/
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value)||(this.right!=null&&this.right.value==value)) {
return this;
}
//查找的值小于当前节点的值，向左查找
if (value < this.value && this.left != null) {
return this.left.searchParent(value);
} else if (value >= this.value && this.right != null) {
//大于当前节点的值，向右查找
return this.right.searchParent(value);
} else {
return null;
}
}
.....
}
2.二叉树实体代码
/**
* 二叉树实体
*/
class BinarySortTree {
Node root;
/**
* 删除节点
*
* @param value 删除的节点值
*/
public void deleteNode(int value) {
if (root == null) {
return;
}
//查找需要删除节点
Node target = root.search(value);
if (target == null) {
//没找到不处理
return;
}
//当只有一个节点并且就是需要删除的节点
if (root.getLeft() == null && root.getRight() == null) {
root = null;
}
//获取需要删除节点的父节点
Node parent = root.searchParent(value);
/*
*第一种情况：当需要删除的节点是叶子节点时
*/
if (target.getLeft() == null && target.getRight() == null) {
if (parent.getLeft() != null && parent.getLeft().getValue() == target.getValue()) {
//当需要删除的节点时父节点的左子节点时
parent.setLeft(null);
}
if (parent.getRight() != null && parent.getRight().getValue() == target.getValue()) {
parent.setRight(null);
}
}
}
测试输出：
public static void main(String[] args) {
int arr[] = {7, 3, 10, 12, 5, 1, 9};
System.out.println("原数组：" + Arrays.toString(arr));
BinarySortTree binarySortTree = new BinarySortTree();
for (int value : arr) {
binarySortTree.add(new Node(value));
}
System.out.println("前序遍历========");
binarySortTree.infixOrder();
System.out.println("\n删除叶子节点============");
System.out.println("删除1节点");
binarySortTree.deleteNode(1);
binarySortTree.infixOrder();
System.out.println("\n删除5节点");
binarySortTree.deleteNode(5);
binarySortTree.infixOrder();
}
输出：
原数组：[7, 3, 10, 12, 5, 1, 9]
前序遍历========
1 3 5 7 9 10 12
删除叶子节点============
删除1节点
3 5 7 9 10 12
删除5节点
3 7 9 10 12
发现已经将叶子节点删除掉了！ 2.删除只有一个节点的树
分为以下四种情况
/**
* 删除节点
*
* @param value 删除的节点值
*/
public void deleteNode(int value) {
if (root == null) {
return;
}
//查找需要删除节点
Node target = root.search(value);
if (target == null) {
//没找到不处理
return;
}
//当只有一个节点并且就是需要删除的节点
if (root.getLeft() == null && root.getRight() == null) {
root = null;
}
//获取需要删除节点的父节点
Node parent = root.searchParent(value);
/*
*第一种情况：当需要删除的节点是叶子节点时
*/
if (target.getLeft() == null && target.getRight() == null) {
if (parent.getLeft() != null && parent.getLeft().getValue() == target.getValue()) {
//当需要删除的节点时父节点的左子节点时
parent.setLeft(null);
}
if (parent.getRight() != null && parent.getRight().getValue() == target.getValue()) {
parent.setRight(null);
}
} else if (target.getLeft() != null && target.getRight() != null) {
//目标节点的两个子节点都不为空
} else {
//重点：删除只有一个节点的子树，分为以下四种情况
//目标节点的一个节点为空
if (target.getLeft() != null) {
//删除目标节点的左子节点不为空
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
//目标节点在父节点的左边
parent.setLeft(target.getLeft());
} else {
//目标节点在父节点的右边
parent.setRight(target.getLeft());
}
} else {
//需要删除的节点有右子节点
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
parent.setLeft(target.getRight());
}else{
parent.setRight(target.getRight());
}
}
}
}
测试：
int arr[] = {7, 3, 10, 12, 5, 1, 9,2};
System.out.println("原数组：" + Arrays.toString(arr));
BinarySortTree binarySortTree = new BinarySortTree();
for (int value : arr) {
binarySortTree.add(new Node(value));
}
System.out.println("前序遍历========");
binarySortTree.infixOrder();
System.out.println("\n删除叶子节点============");
//删除1节点
binarySortTree.deleteNode(1);
binarySortTree.infixOrder();
测试输出：
原数组：[7, 3, 10, 12, 5, 1, 9, 2]
前序遍历========
1 2 3 5 7 9 10 12
删除叶子节点============
1 3 5 7 9 10 12
发现确实把1节点删掉了 
其他情况测试后也复合预期！
3.删除有两个子树的节点
代码示例：
定义一个方法
/**
* 1.返回以目标节点为根节点的二叉排序树的最小节点的值
* 2.删除目标节点为根节点的二叉排序树的最小节点
*
* @param node 目标节点的右子树节点
* @return 右子树的最小值
*/
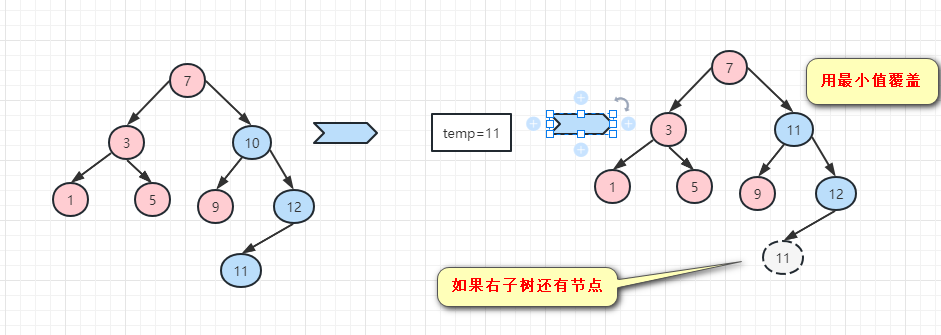
public int delRightTreeMin(Node node) {
Node target = node;
//循环查找右子树中的左子树，找到的就是最小值
while (target.getLeft() != null) {
target = target.getLeft();
}
//删除最小节点
/*
思考点1：这里的代码为啥不直接写在删除代码中，而是抽取成一个方法呢
如果写在删除deleteNode方法中，那方法中就是递归调用，没有像方法返回一个唯一的值
回溯时可能会存在多次赋值的情况！
*/
deleteNode(target.getValue());
return target.getValue();
}
最终的删除节点方法
/**
* 删除节点
*
* @param value 删除的节点值
*/
public void deleteNode(int value) {
if (root == null) {
return;
}
//查找需要删除节点
Node target = root.search(value);
if (target == null) {
//没找到不处理
return;
}
//当只有一个节点并且就是需要删除的节点
if (root.getLeft() == null && root.getRight() == null) {
root = null;
}
//获取需要删除节点的父节点
Node parent = root.searchParent(value);
/*
*第一种情况：当需要删除的节点是叶子节点时
*/
if (target.getLeft() == null && target.getRight() == null) {
if (parent.getLeft() != null && parent.getLeft().getValue() == target.getValue()) {
//当需要删除的节点时父节点的左子节点时
parent.setLeft(null);
}
if (parent.getRight() != null && parent.getRight().getValue() == target.getValue()) {
parent.setRight(null);
}
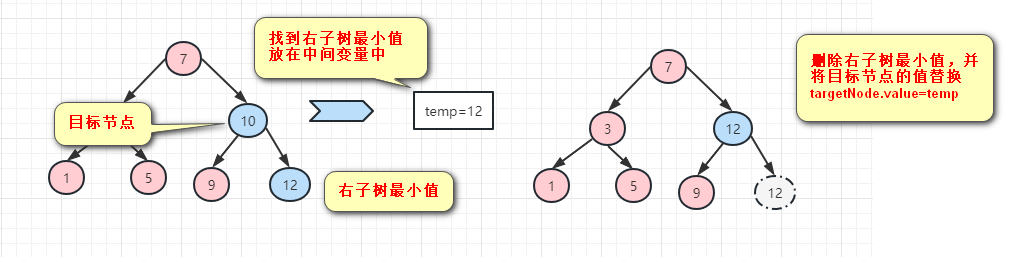
} else if (target.getLeft() != null && target.getRight() != null) {
//目标节点的两个子节点都不为空,在右子树上找最小的值
int rightTreeMinValue = delRightTreeMin(target.getRight());
target.setValue(rightTreeMinValue);
} else {
//目标节点的一个节点为空
if (target.getLeft() != null) {
//删除目标节点的左子节点不为空
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
//目标节点在父节点的左边
parent.setLeft(target.getLeft());
} else {
//目标节点在父节点的右边
parent.setRight(target.getLeft());
}
} else {
//需要删除的节点有右子节点
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
parent.setLeft(target.getRight());
} else {
parent.setRight(target.getRight());
}
}
}
}
}
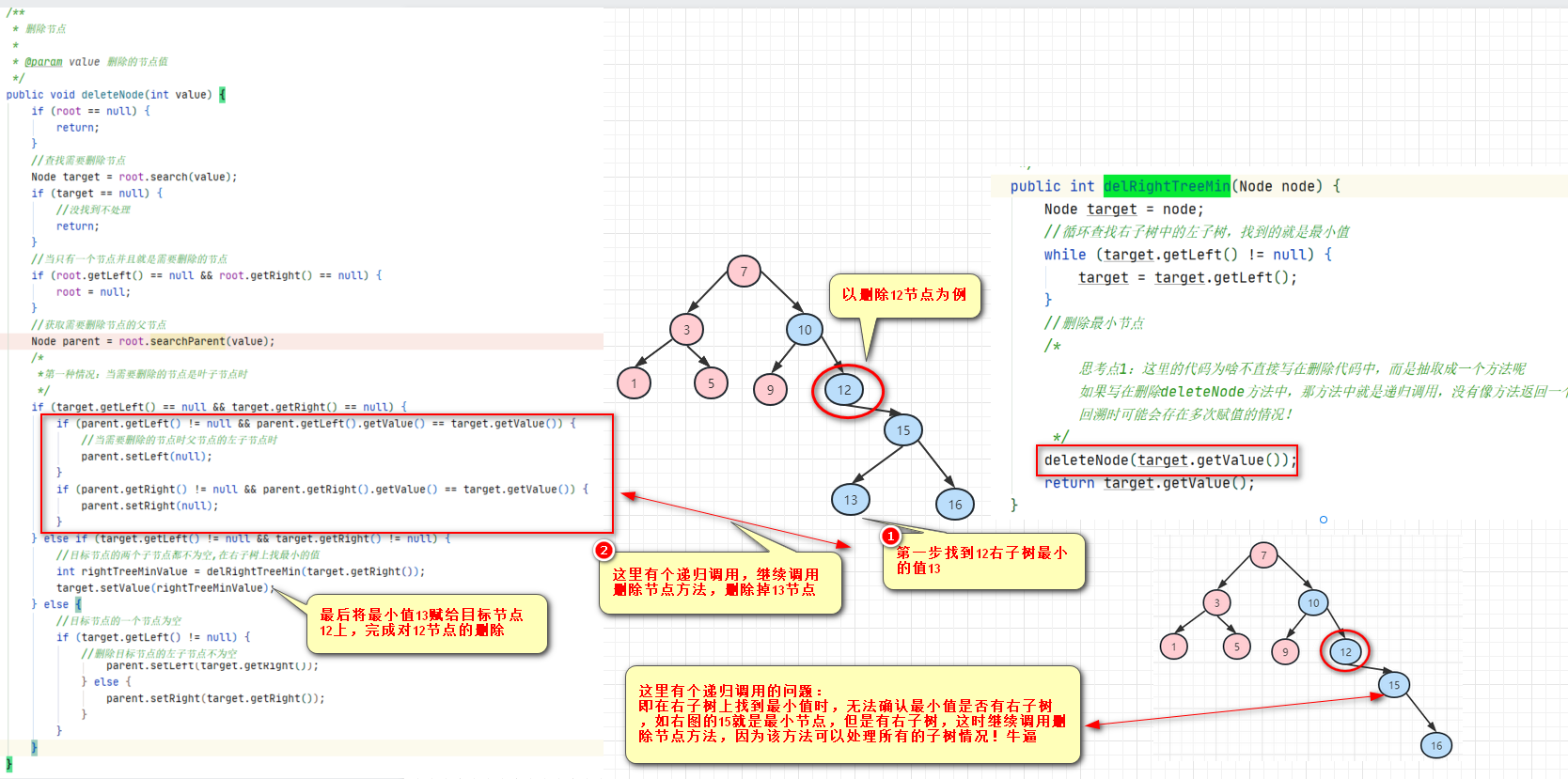
改进：上述代码删除只有一个子树的节点时有个问题可能会报空指针！
改进到最终方案：
/**
* 删除节点
*
* @param value 删除的节点值
*/
public void deleteNode(int value) {
if (root == null) {
return;
}
//查找需要删除节点
Node target = root.search(value);
if (target == null) {
//没找到不处理
return;
}
//当只有一个节点并且就是需要删除的节点
if (root.getLeft() == null && root.getRight() == null) {
root = null;
}
//获取需要删除节点的父节点
Node parent = root.searchParent(value);
/*
*第一种情况：当需要删除的节点是叶子节点时
*/
if (target.getLeft() == null && target.getRight() == null) {
if (parent.getLeft() != null && parent.getLeft().getValue() == target.getValue()) {
//当需要删除的节点时父节点的左子节点时
parent.setLeft(null);
}
if (parent.getRight() != null && parent.getRight().getValue() == target.getValue()) {
parent.setRight(null);
}
} else if (target.getLeft() != null && target.getRight() != null) {
//目标节点的两个子节点都不为空,在右子树上找最小的值
int rightTreeMinValue = delRightTreeMin(target.getRight());
target.setValue(rightTreeMinValue);
} else {
//目标节点的一个节点为空
if (target.getLeft() != null) {
if (parent != null) {
//删除目标节点的左子节点不为空
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
//目标节点在父节点的左边
parent.setLeft(target.getLeft());
} else {
//目标节点在父节点的右边
parent.setRight(target.getLeft());
}
} else {
root = target.getLeft();
}
} else {
if (parent !=null){
//需要删除的节点有右子节点
if (parent.getLeft() != null && parent.getLeft().getValue() == value) {
parent.setLeft(target.getRight());
} else {
parent.setRight(target.getRight());
}
}else {
root=target.getRight();
}
}
}
}
