12.树结构-二叉树-赫夫曼树

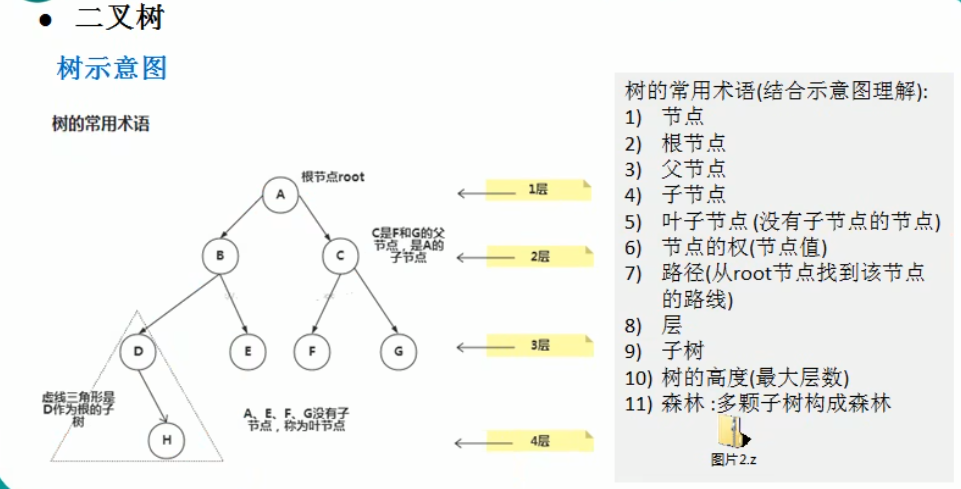
二叉树
1.概念
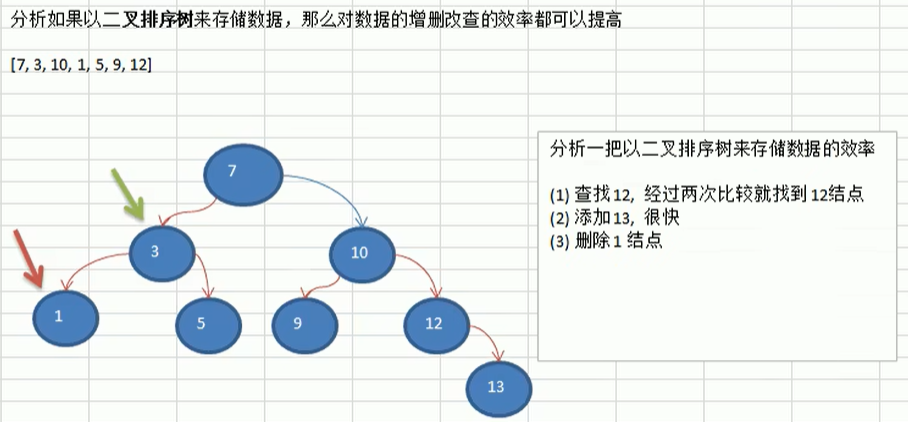
1.数有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。
2.二叉树的子节点分为左节点和右节点。
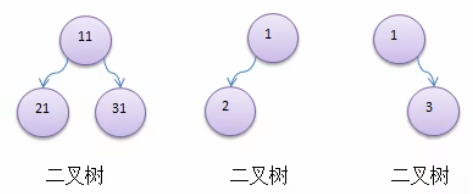
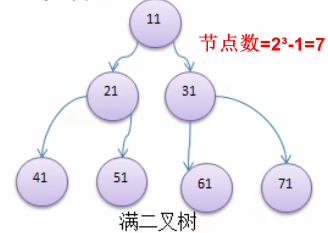
3.如果该二叉树的所有叶子节点都在最后一层,并且总节点数为=2ⁿ-1,n为层数,则我们称为满二叉树
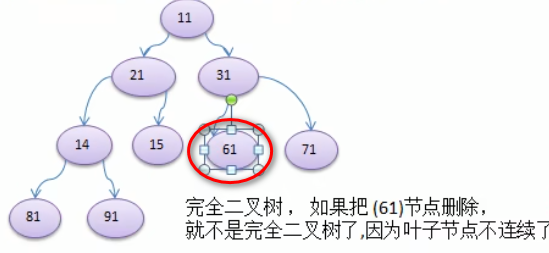
4.如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,我们称之为完全二叉树。
2.遍历二叉树
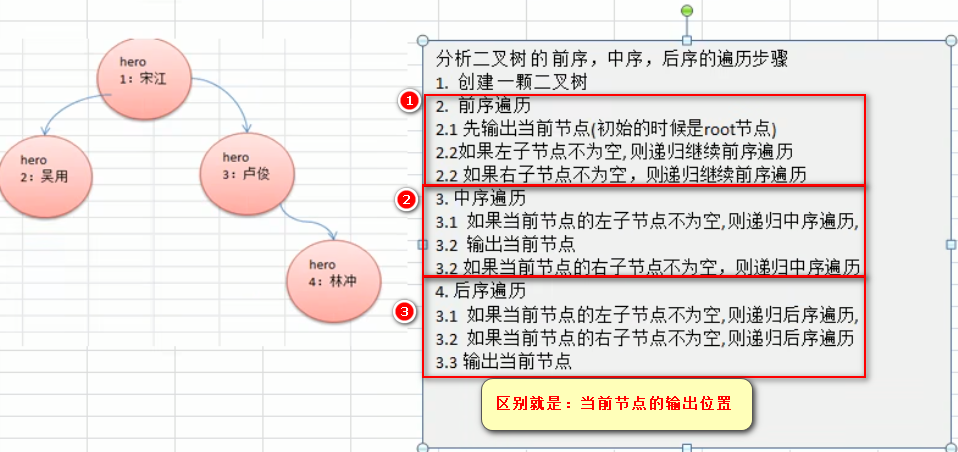
1.前序遍历:先输出父节点,再遍历左子树和右子树
2.中序遍历:先遍历左子树,再输出父节点,再遍历右子树
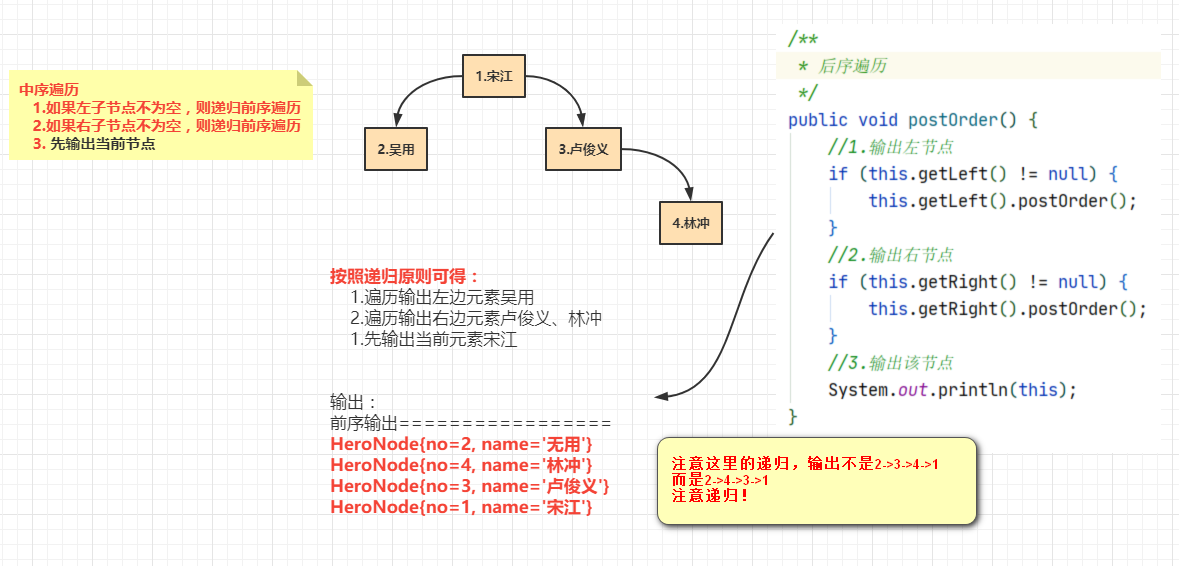
3.后序遍历:先遍历左子树,在遍历右子树,最后输出父节点
小结:
看父节点的输出顺序,确定是前序、中序、后序
示例:
public class BinaryTreeDemo {
public static void main(String[] args) {
HeroNode root = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "无用");
HeroNode heroNode3 = new HeroNode(3, "卢俊义");
HeroNode heroNode4 = new HeroNode(4, "林冲");
root.setLeft(heroNode2);
root.setRight(heroNode3);
heroNode3.setRight(heroNode4);
BinaryTree tree=new BinaryTree(root);
//前序输出
System.out.println("前序输出=================");
tree.preOrder();
System.out.println("中序输出==================");
tree.infixOrder();
System.out.println("后序输出==================");
tree.postOrder();
}
}
/**
* 树结构
*/
class BinaryTree {
//根节点
HeroNode root;
public BinaryTree(HeroNode root) {
this.root = root;
}
/**
* 前序遍历
*/
public void preOrder() {
root.preOrder();
}
/**
* 中序遍历
*/
public void infixOrder() {
root.infixOrder();
}
/**
* 后续遍历
*/
public void postOrder() {
root.postOrder();
}
}
/**
* 实体节点
*/
class HeroNode {
//编号
private int no;
//名称
private String name;
//左节点
private HeroNode left;
//右节点
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
/**
* 前序遍历
*/
public void preOrder() {
//1.先输出当前节点
System.out.println(this);
//2.输出左节点
if (this.getLeft() != null) {
this.getLeft().preOrder();
}
//2.输出右节点
if (this.getRight() != null) {
this.getRight().preOrder();
}
}
/**
* 中序遍历
*/
public void infixOrder() {
//1.输出左节点
if (this.getLeft() != null) {
this.getLeft().infixOrder();
}
//2.输出本节点
System.out.println(this);
//3.输出右节点
if (this.getRight() != null) {
this.getRight().infixOrder();
}
}
/**
* 后续遍历
*/
public void postOrder() {
//1.输出左节点
if (this.getLeft() != null) {
this.getLeft().postOrder();
}
//2.输出右节点
if (this.getRight() != null) {
this.getRight().postOrder();
}
//3.输出该节点
System.out.println(this);
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
}
输出;
前序输出=================
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=4, name='林冲'}
中序输出==================
HeroNode{no=2, name='无用'}
HeroNode{no=1, name='宋江'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=4, name='林冲'}
后序输出==================
HeroNode{no=2, name='无用'}
HeroNode{no=4, name='林冲'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=1, name='宋江'}1.前序遍历分析
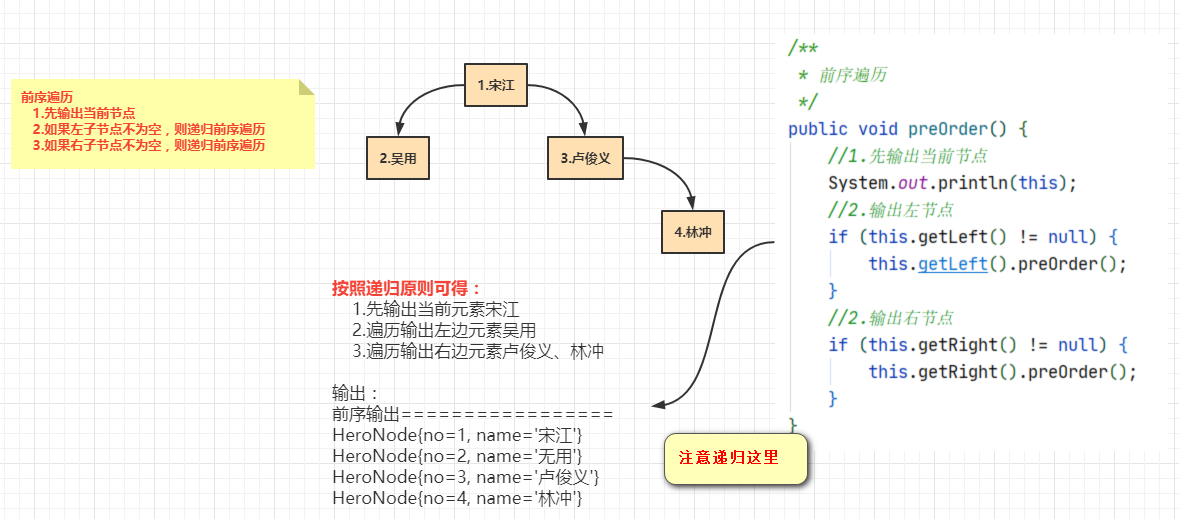
2.中序遍历分析
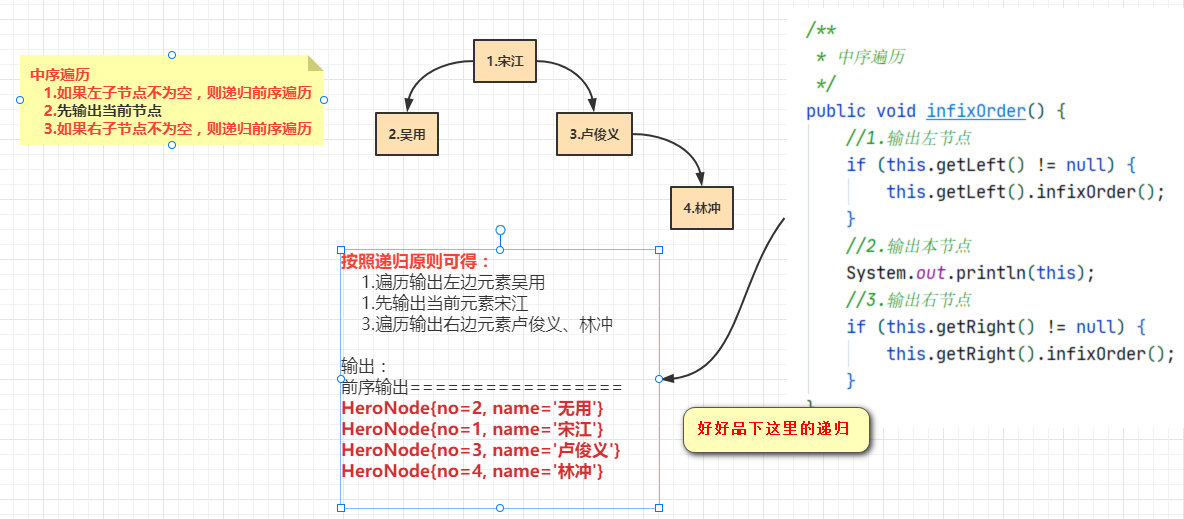
3.后序遍历分析
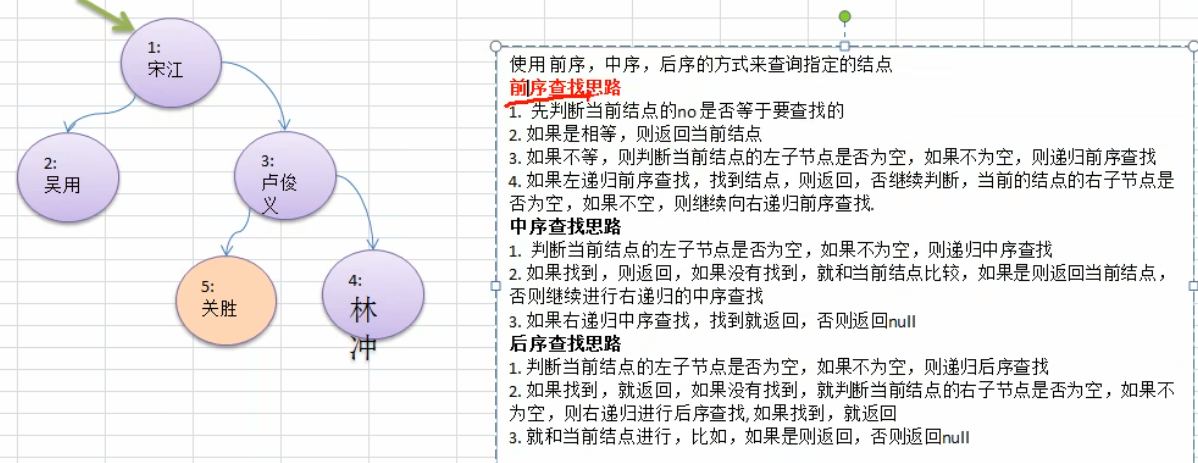
查找指定节点
1.前序查找代码
1.实体代码
/**
* 实体节点
*/
class HeroNode {
...
/**
* 前序遍历
*
* @param no 查找的英雄编号
*/
public HeroNode preOrderSearch(int no) {
System.out.println("----->前序查找");
//1.判断当前对象是否符合
if (this.getNo() == no) {
return this;
}
HeroNode node = null;
//2.左遍历
if (this.getLeft() != null) {
node = this.getLeft().preOrderSearch(no);
}
//找到了结束递归
if (node != null) {
return node;
}
//3.没找到,右遍历
if (this.getRight() != null) {
node = this.getRight().preOrderSearch(no);
}
return node;
}
...
}
2.树的代码
/**
* 前序查找
*
* @param no 查找编号
* @return
*/
public HeroNode preOrderSearch(int no) {
return root.preOrderSearch(no);
}
3.查找代码
public static void main(String[] args) {
HeroNode root = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "无用");
HeroNode heroNode3 = new HeroNode(3, "卢俊义");
HeroNode heroNode4 = new HeroNode(4, "林冲");
HeroNode heroNode5 = new HeroNode(5, "关胜");
root.setLeft(heroNode2);
root.setRight(heroNode3);
heroNode3.setRight(heroNode4);
heroNode3.setLeft(heroNode5);
BinaryTree tree = new BinaryTree(root);
HeroNode heroNode = tree.preOrderSearch(5);
if (heroNode != null)
System.out.println(heroNode.toString());
}
输出:发现进行了四次比较
----->前序查找
----->前序查找
----->前序查找
----->前序查找
HeroNode{no=5, name='关胜'}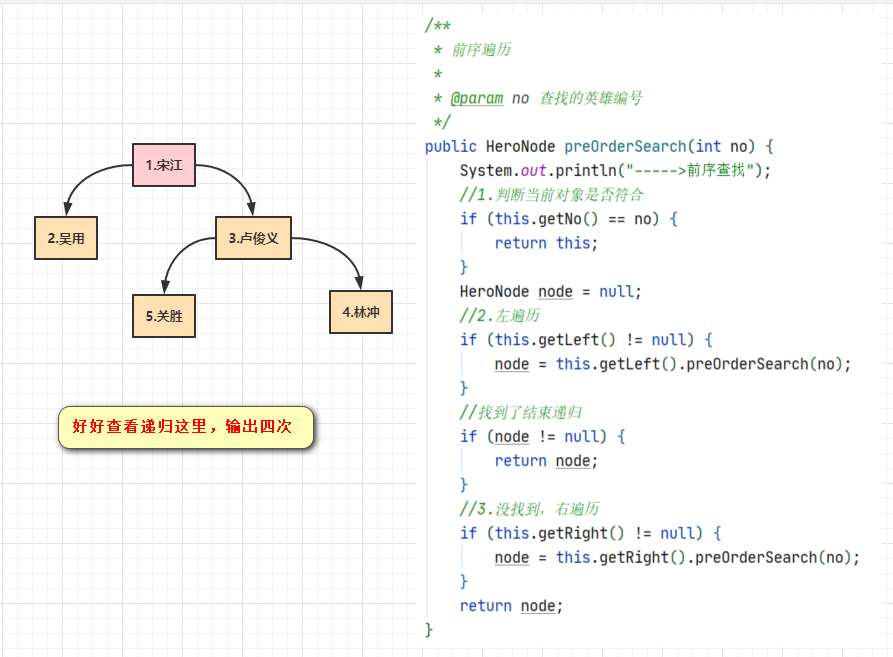
2.中序查找代码
1.实体类中的查找方法
/**
* 中序查找
*
* @param no 查找编号
*/
public HeroNode infixOrderSearch(int no) {
HeroNode node = null;
//1.左查找
if (this.getLeft() != null) {
node = this.getLeft().infixOrderSearch(no);
}
//查找到了
if (node != null) {
return node;
}
//2.查看当前节点
System.out.println("中序查找------->"+this.toString());
if (this.getNo() == no) {
return this;
}
//3.没找到,右遍历
if (this.getRight() != null) {
node = this.getRight().infixOrderSearch(no);
}
return node;
}
2.树类代码
/**
* 中序查找
*
* @param no 查找编号
*/
public HeroNode infixOrderSearch(int no) {
return root.infixOrderSearch(no);
}
3.测试;
public static void main(String[] args) {
HeroNode root = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "无用");
HeroNode heroNode3 = new HeroNode(3, "卢俊义");
HeroNode heroNode4 = new HeroNode(4, "林冲");
HeroNode heroNode5 = new HeroNode(5, "关胜");
root.setLeft(heroNode2);
root.setRight(heroNode3);
heroNode3.setRight(heroNode4);
heroNode3.setLeft(heroNode5);
BinaryTree tree = new BinaryTree(root);
HeroNode heroNode = tree.infixOrderSearch(5);
if (heroNode != null)
System.out.println(heroNode.toString());
}
输出:三次比较
中序查找------->HeroNode{no=2, name='无用'}
中序查找------->HeroNode{no=1, name='宋江'}
中序查找------->HeroNode{no=5, name='关胜'}
HeroNode{no=5, name='关胜'} 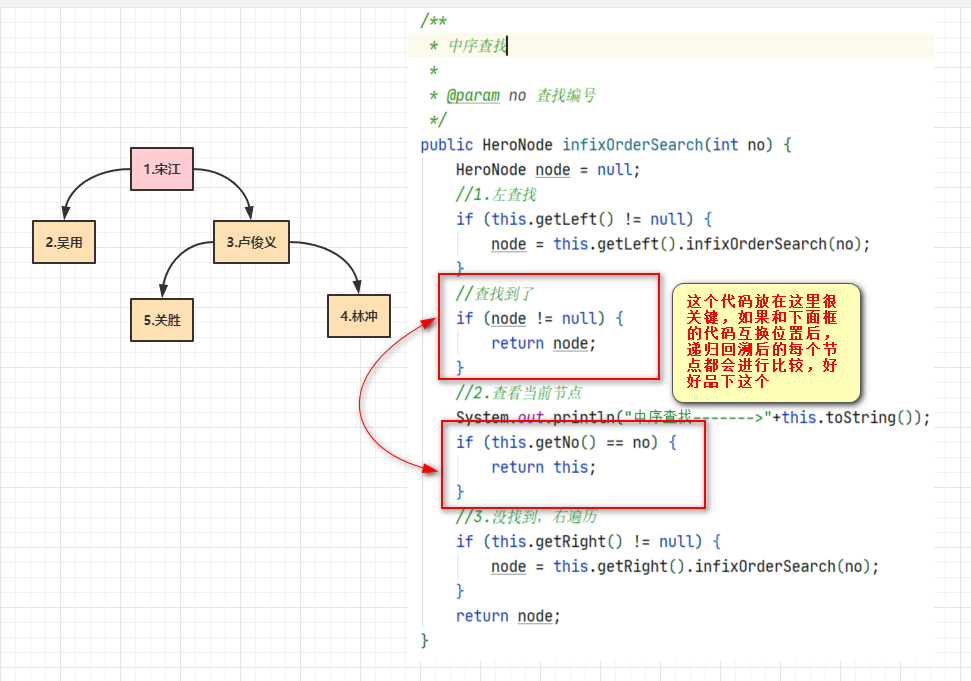
3.后序查找代码
实体类代码:
/**
* 后序查找
*
* @param no 查找编号
*/
public HeroNode postOrderSearch(int no) {
HeroNode node = null;
//找左边
if (this.getLeft() != null) {
node = this.getLeft().postOrderSearch(no);
}
if (node != null) {
return node;
}
//找右边
if (this.getRight() != null) {
node = this.getRight().postOrderSearch(no);
}
if (node != null) {
return node;
}
System.out.println("后序查找---->" + this.toString());
if (this.getNo() == no) {
node = this;
}
return node;
}
树代码:
/**
* 后序查找
*
* @param no 查找编号
*/
public HeroNode postOrderSearch(int no) {
return root.postOrderSearch(no);
}
测试代码:
public static void main(String[] args) {
HeroNode root = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "无用");
HeroNode heroNode3 = new HeroNode(3, "卢俊义");
HeroNode heroNode4 = new HeroNode(4, "林冲");
HeroNode heroNode5 = new HeroNode(5, "关胜");
root.setLeft(heroNode2);
root.setRight(heroNode3);
heroNode3.setRight(heroNode4);
heroNode3.setLeft(heroNode5);
BinaryTree tree = new BinaryTree(root);
HeroNode heroNode = tree.postOrderSearch(5);
if (heroNode != null)
System.out.println(heroNode.toString());
}
输出:两次比较
后序查找---->HeroNode{no=2, name='无用'}
后序查找---->HeroNode{no=5, name='关胜'}
HeroNode{no=5, name='关胜'}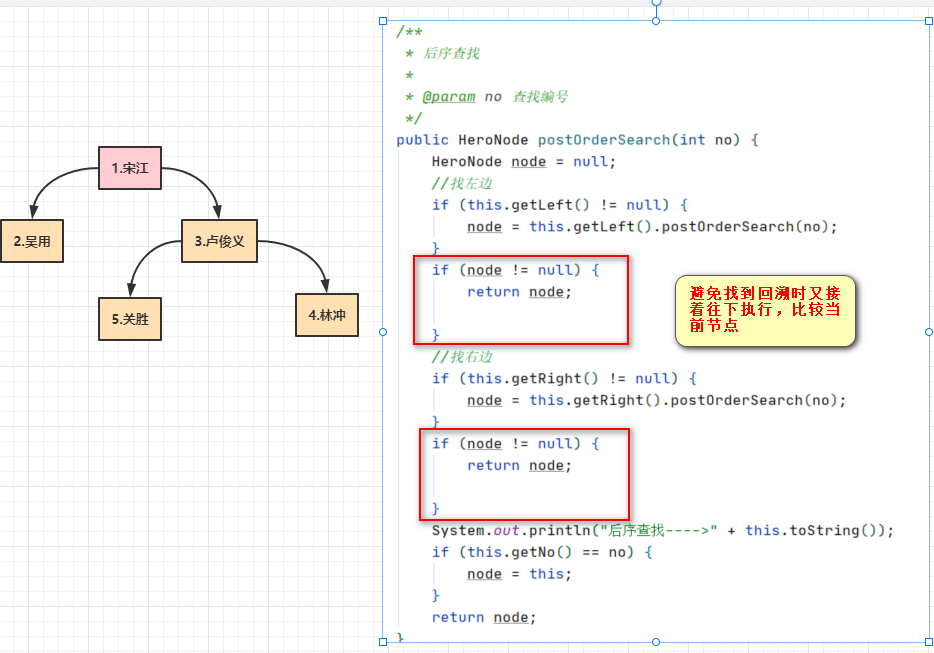
二叉树-删除节点
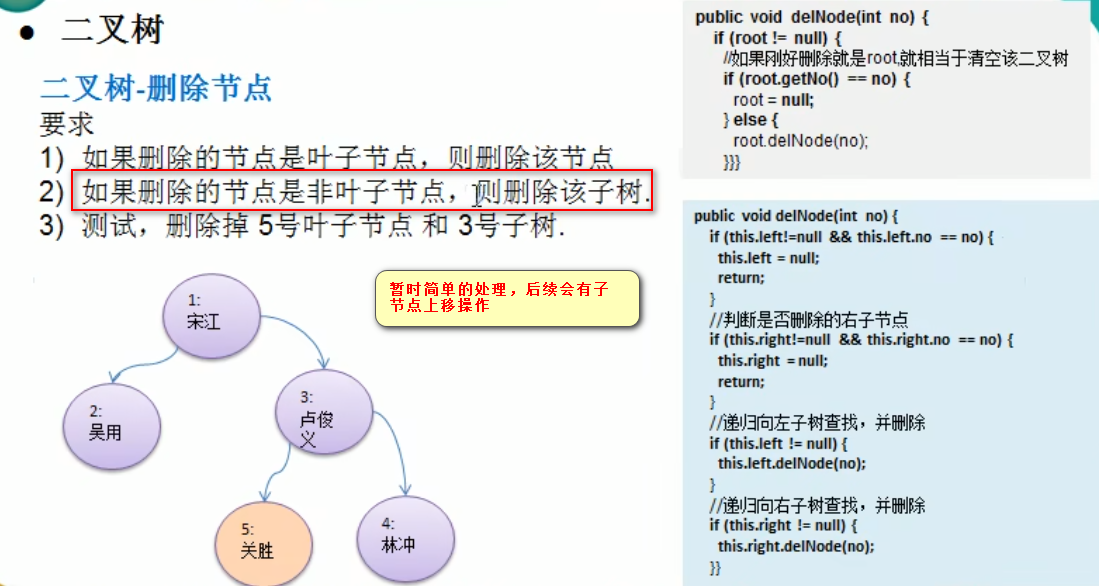

代码示例
实体类代码:
/**
* 删除
*
* @param no 编号
*/
public void deleteByNo(int no) {
/*
思路:
1.因为我们的二叉树是单向的,所以我们是判断当前节点的子节点是否是删除的no,
2.如果当前节点的左子节点不为空,并且左子节点就是要删除的节点,就将this.left=null;并返回(结束递归)
3.如果当前节点的右子节点不为空,并且右子节点就是要删除的节点,就将this.right=null;并返回
4.如果第二,三步没有删除节点,就向左子树进行递归删除。
5.以上四步都没有删除节点,应该向右子树行递归删除。
*/
if (this.getLeft() != null && this.getLeft().getNo() == no) {
this.setLeft(null);
return;
}
if (this.getRight() != null && this.getRight().getNo() == no) {
this.setRight(null);
return;
}
if (this.getLeft() != null) {
this.getLeft().deleteByNo(no);
}
if (this.getRight() != null) {
this.getRight().deleteByNo(no);
}
}
树类代码:
/**
* 根据no删除
*
* @param no
*/
public void deleteByNo(int no) {
if (root.getNo() == no) {
root = null;
return;
}
root.deleteByNo(no);
}
测试类代码:
public static void main(String[] args) {
HeroNode root = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "无用");
HeroNode heroNode3 = new HeroNode(3, "卢俊义");
HeroNode heroNode4 = new HeroNode(4, "林冲");
HeroNode heroNode5 = new HeroNode(5, "关胜");
HeroNode heroNode6 = new HeroNode(6, "李青");
HeroNode heroNode7 = new HeroNode(7, "李逵");
root.setLeft(heroNode2);
root.setRight(heroNode3);
heroNode3.setRight(heroNode4);
heroNode3.setLeft(heroNode5);
heroNode5.setLeft(heroNode6);
heroNode4.setRight(heroNode7);
BinaryTree tree = new BinaryTree(root);
tree.preOrder();
System.out.println("删除=====>");
tree.deleteByNo(6);
tree.preOrder();
}
输出:发现6号节点已经删除
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=5, name='关胜'}
HeroNode{no=6, name='李青'}
HeroNode{no=4, name='林冲'}
HeroNode{no=7, name='李逵'}
删除=====>
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=5, name='关胜'}
HeroNode{no=4, name='林冲'}
HeroNode{no=7, name='李逵'}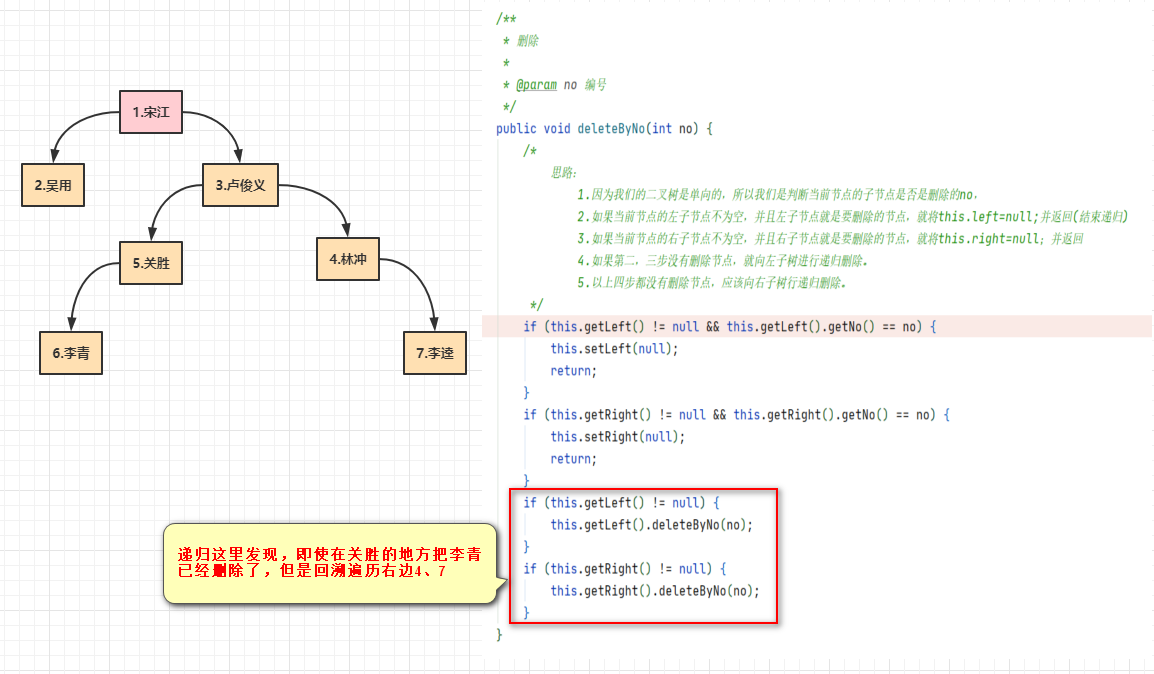
问题:
即使左边找到节点已经删除,还是会回溯到右边进行删除!这是个问题,看后续学习看能解决不!
删除非叶子节点
tree.deleteByNo(3);
按照设计逻辑会把子树整个删掉
输出:
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=5, name='关胜'}
HeroNode{no=6, name='李青'}
HeroNode{no=4, name='林冲'}
HeroNode{no=7, name='李逵'}
删除=====>
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}对于上述改进,删除非叶子节点
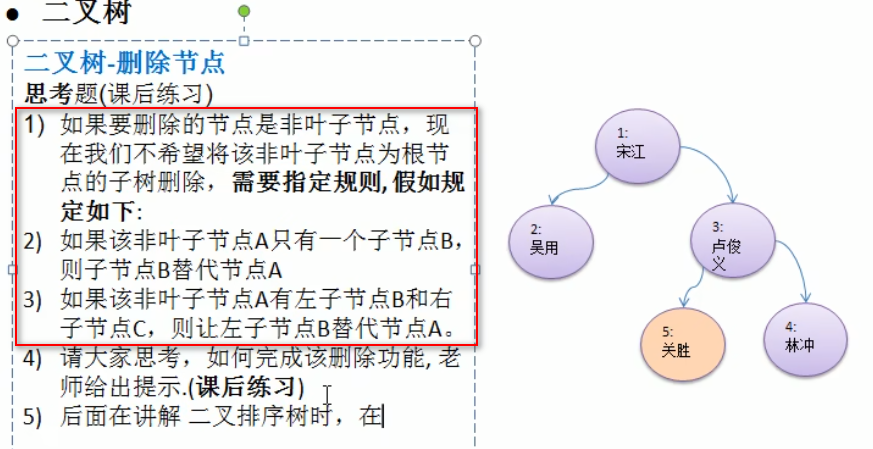
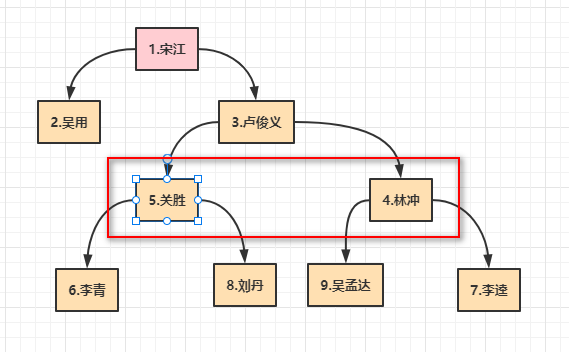
删除5或者4
实体类改造:
/**
* 删除
*
* @param no 编号
*/
public void deleteByNo(int no) {
/*
思路:
改造点
*/
if (this.getLeft() != null && this.getLeft().getNo() == no) {
HeroNode heroNode = this.getLeft();
//1.叶子节点
if (heroNode.getLeft() == null && heroNode.getRight() == null) {
this.setLeft(null);
} else if (heroNode.getLeft() != null && heroNode.getRight() != null) {
HeroNode right = heroNode.getRight();
//非叶子节点,并且左右都有,左边节点代替删除节点
this.setLeft(heroNode.getLeft());
this.getLeft().setRight(right);
} else if (this.getLeft().getLeft() != null) {
//左子节点不为空,右节点为空
this.setLeft(heroNode.getLeft());
} else {
//左子节点为空,右节点不为空
this.setLeft(heroNode.getRight());
}
return;
}
//这个处理和上面一样
if (this.getRight() != null && this.getRight().getNo() == no) {
HeroNode heroNode = this.getRight();
//叶子节点
if (heroNode.getLeft() == null && heroNode.getRight() == null) {
this.setRight(null);
} else if (heroNode.getLeft() != null && heroNode.getRight() != null) {
HeroNode right = heroNode.getRight();
this.setRight(heroNode.getLeft());
this.getRight().setRight(right);
} else if (heroNode.getLeft() != null) {
this.setRight(heroNode.getLeft());
} else {
this.setRight(heroNode.getRight());
}
return;
}
if (this.getLeft() != null) {
this.getLeft().deleteByNo(no);
}
if (this.getRight() != null) {
this.getRight().deleteByNo(no);
}
}
测试:
public class BinaryTreeDemo {
public static void main(String[] args) {
HeroNode root = new HeroNode(1, "宋江");
HeroNode heroNode2 = new HeroNode(2, "无用");
HeroNode heroNode3 = new HeroNode(3, "卢俊义");
HeroNode heroNode4 = new HeroNode(4, "林冲");
HeroNode heroNode5 = new HeroNode(5, "关胜");
HeroNode heroNode6 = new HeroNode(6, "李青");
HeroNode heroNode7 = new HeroNode(7, "李逵");
HeroNode heroNode8 = new HeroNode(8, "刘丹");
HeroNode heroNode9 = new HeroNode(9, "吴孟达");
root.setLeft(heroNode2);
root.setRight(heroNode3);
heroNode3.setRight(heroNode4);
heroNode3.setLeft(heroNode5);
heroNode5.setLeft(heroNode6);
heroNode4.setRight(heroNode7);
heroNode5.setRight(heroNode8);
heroNode4.setLeft(heroNode9);
BinaryTree tree = new BinaryTree(root);
System.out.println("删除=====>");
tree.deleteByNo(5);
tree.preOrder();
}
输出:发现5号节点已删除,但是子树还在!
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=5, name='关胜'}
HeroNode{no=6, name='李青'}
HeroNode{no=8, name='刘丹'}
HeroNode{no=4, name='林冲'}
HeroNode{no=9, name='吴孟达'}
HeroNode{no=7, name='李逵'}
删除=====>
HeroNode{no=1, name='宋江'}
HeroNode{no=2, name='无用'}
HeroNode{no=3, name='卢俊义'}
HeroNode{no=6, name='李青'}
HeroNode{no=8, name='刘丹'}
HeroNode{no=4, name='林冲'}
HeroNode{no=9, name='吴孟达'}
HeroNode{no=7, name='李逵'}顺序存储二叉树
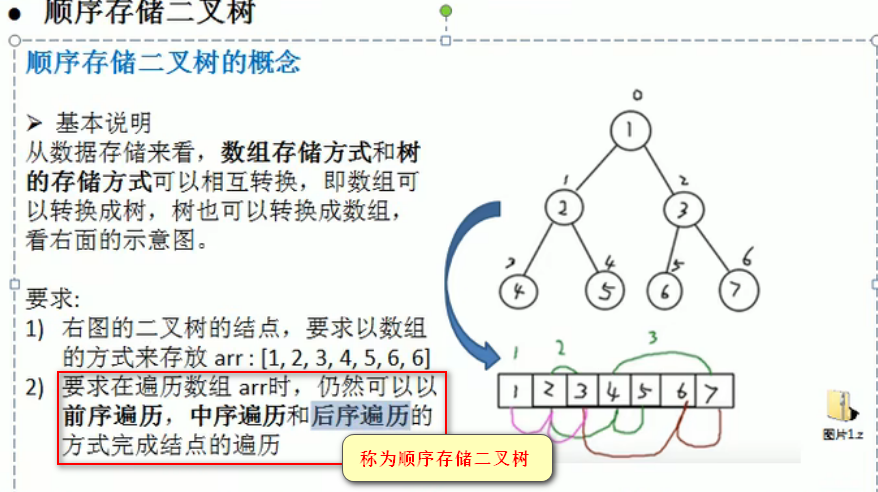

需求:
给定一个数组{1,2,3,4,5,6,7},要求以二叉树前序遍历的方式进行遍历输出
/**
* 顺序存储二叉树方式的前序输出数组
*/
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int arr[] = {1, 2, 3, 4, 5, 6, 7};
System.out.println("原数组:"+ Arrays.toString(arr));
ArrBinaryTree tree=new ArrBinaryTree(arr);
tree.preOrder(0);
}
}
class ArrBinaryTree {
int arr[] = null;
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
/**
* 按照树的前序输出数组
*
* @param index 数组下标
*/
public void preOrder(int index) {
if (arr == null || arr.length == 0) {
return;
}
System.out.print(arr[index]+" ");
//左遍历
if ((2 * index + 1) < arr.length) {
preOrder(2 * index + 1);
}
//右遍历
if ((2 * index + 2) < arr.length) {
preOrder(2 * index + 2);
}
}
}
输出:
原数组:[1, 2, 3, 4, 5, 6, 7]
1 2 4 5 3 6 7 中序遍历和后序遍历只需要更改代码输出位置即可!
线索化二叉树
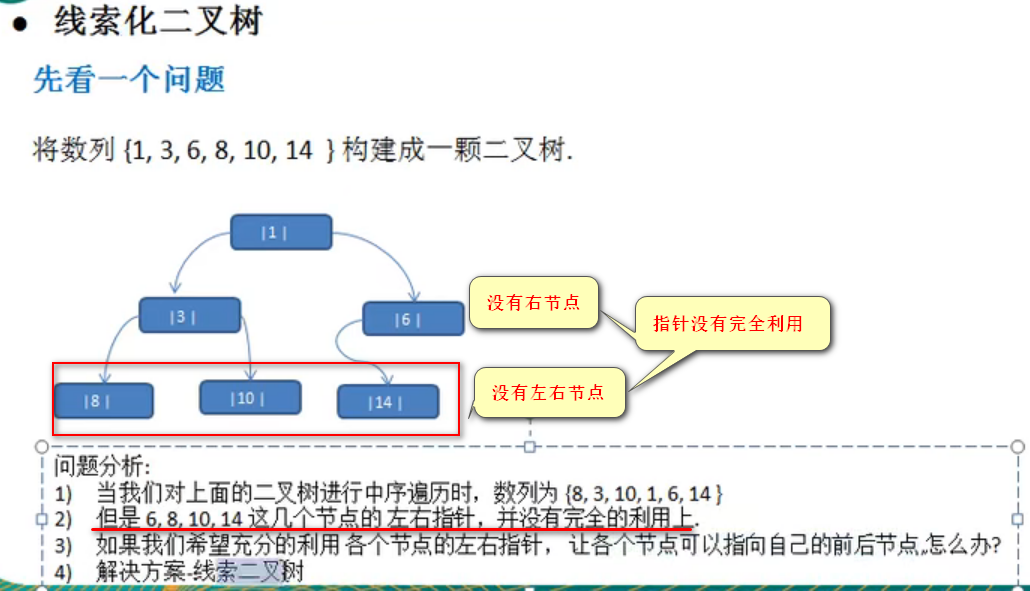

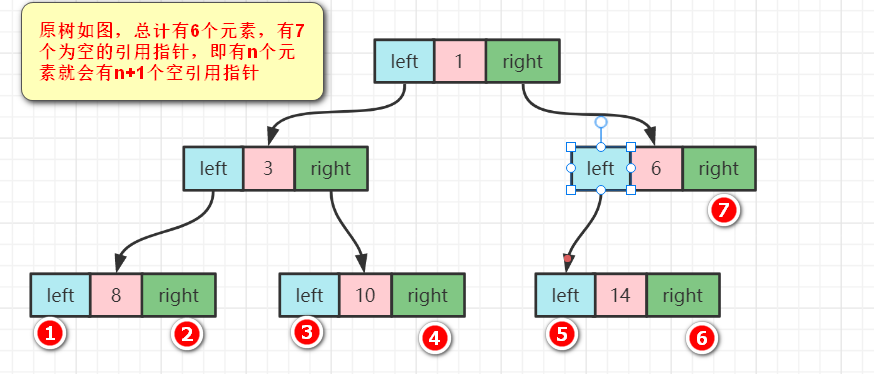
例如上述数列按照中序遍历时输出:{8,3,10,1,6,14}
6称为14的前驱节点,14称为6的后继节点,并不是按照树的父子节点来论的!
案例:
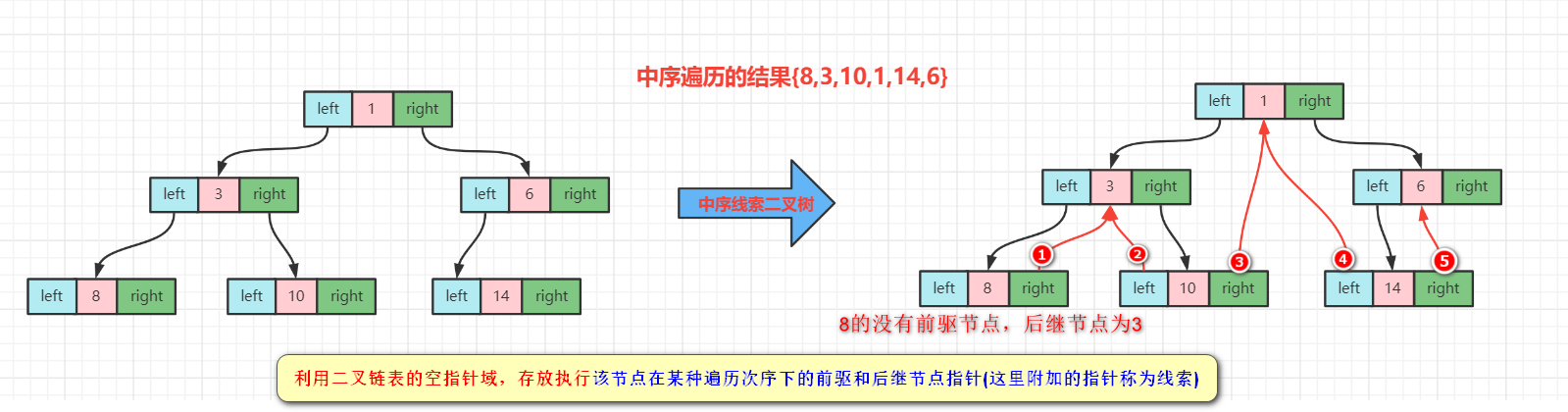
说明:node节点的left和right可能指向子树,也可能指向前驱、后继节点,具体如下
1.left指向的是左子树,也有可能指向前驱节点,例如1节点,left指向左子树,而10节点的left指向的就是前驱节点
2.right指向的是右子树,也可能指向后继节点,比如1节点right指向的是右子树,而10节点的right指向的是后继节点
样例代码:
public class ThreadedBinaryThreeDemo {
public static void main(String[] args) {
HeroNode root = new HeroNode(1);
HeroNode node3 = new HeroNode(3);
HeroNode node6 = new HeroNode(6);
HeroNode node8 = new HeroNode(8);
HeroNode node10 = new HeroNode(10);
HeroNode node14 = new HeroNode(14);
root.setLeft(node3);
root.setRight(node6);
node3.setLeft(node8);
node3.setRight(node10);
node6.setLeft(node14);
BinaryTree binaryTree=new BinaryTree(root);
binaryTree.threadedNodes(root);
System.out.println(node10.getRight());
}
}
class BinaryTree {
//根元素
private HeroNode root;
//上一个元素
private HeroNode pre;
public BinaryTree(HeroNode root) {
this.root = root;
}
//重点:线索化二叉树,这里好好理解下递归,不是很好理解
public void threadedNodes(HeroNode node) {
if (node == null) {
return;
}
//1.先线索化左子树
threadedNodes(node.getLeft());
//2.处理当前节点
//处理前驱节点
if (node.getLeft() == null) {
node.setLeft(pre);
node.setLeftType(1);
}
if (pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRightType(1);
}
pre = node;
//线索化右子树
threadedNodes(node.getRight());
}
}
class HeroNode {
private int no;
private HeroNode left;
private HeroNode right;
//左节点类型:0为子树, 1为前驱后继节点
private int leftType;
//左节点类型:0为子树, 1为前驱后继节点
private int rightType;
public HeroNode(int no) {
this.no = no;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
'}';
}
}
输出:符合预期
10的前驱节点是:HeroNode{no=3}
10的后继节点是:HeroNode{no=1}理解:
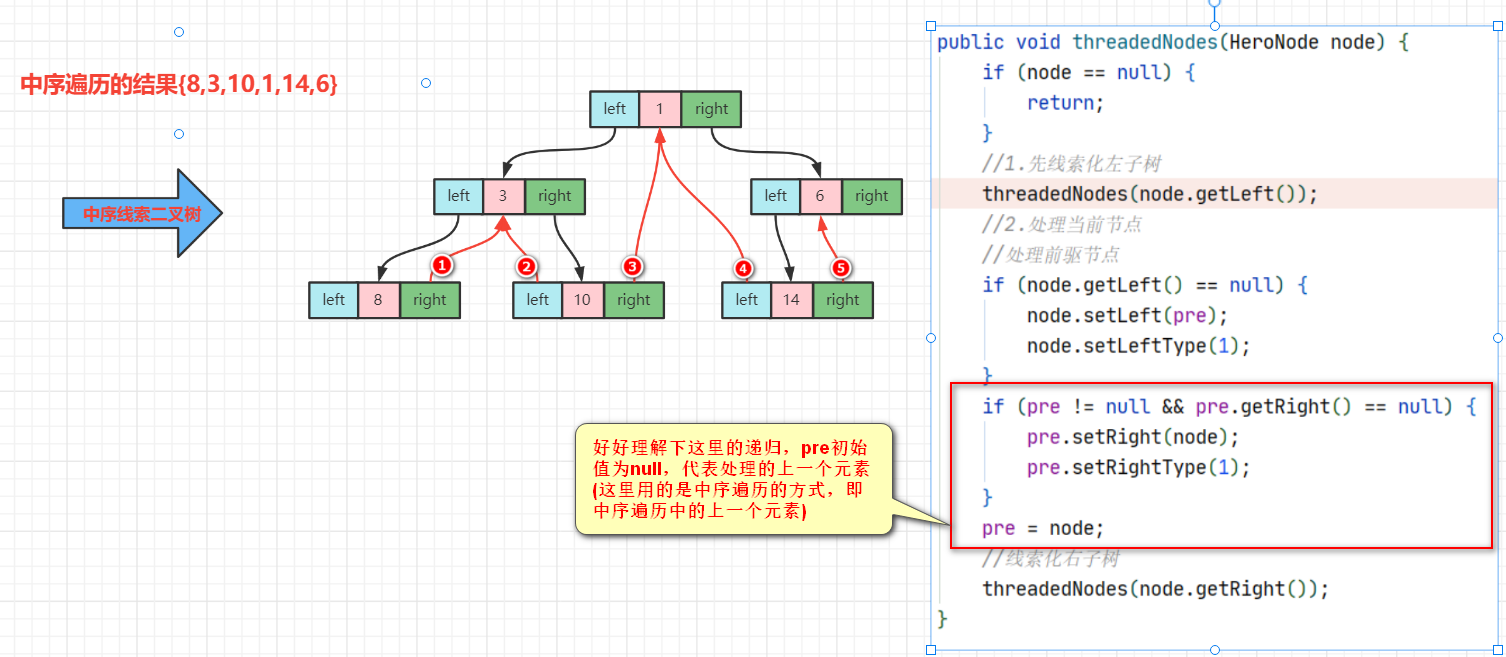
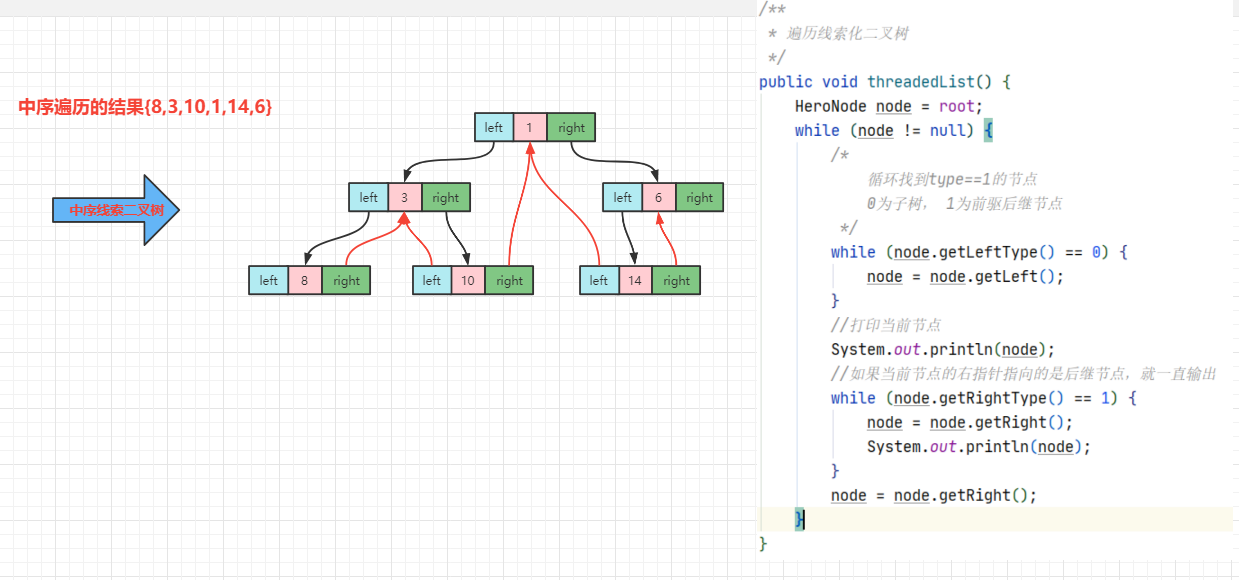
线索化二叉树的遍历
说明:对前面的中序线索化的二叉树进行遍历
分析:因为线索化后,各个节点指向有所变化,因此原来的遍历方式不能使用,这时需要使用新的方式遍历线索化二叉树。各个节点可以通过线性方式遍历
因此无需使用递归方式,这样也提高了遍历的效率,遍历的次序应当和中序遍历保持一致。
代码:
/**
* 遍历线索化二叉树
*/
public void threadedList() {
HeroNode node = root;
while (node != null) {
/*
循环找到type==1的节点
0为子树, 1为前驱后继节点
*/
while (node.getLeftType() == 0) {
node = node.getLeft();
}
//打印当前节点
System.out.println(node);
//如果当前节点的右指针指向的是后继节点,就一直输出
while (node.getRightType() == 1) {
node = node.getRight();
System.out.println(node);
}
node = node.getRight();
}
}
测试输出:
public static void main(String[] args) {
HeroNode root = new HeroNode(1);
HeroNode node3 = new HeroNode(3);
HeroNode node6 = new HeroNode(6);
HeroNode node8 = new HeroNode(8);
HeroNode node10 = new HeroNode(10);
HeroNode node14 = new HeroNode(14);
root.setLeft(node3);
root.setRight(node6);
node3.setLeft(node8);
node3.setRight(node10);
node6.setLeft(node14);
BinaryTree binaryTree = new BinaryTree(root);
binaryTree.threadedNodes(root);
System.out.println("10的前驱节点是:" + node10.getLeft());
System.out.println("10的后继节点是:" + node10.getRight());
System.out.println("线索化二叉树遍历--->");
binaryTree.threadedList();
}
输出:符合预期
10的前驱节点是:HeroNode{no=3}
10的后继节点是:HeroNode{no=1}
线索化二叉树遍历--->
HeroNode{no=8}
HeroNode{no=3}
HeroNode{no=10}
HeroNode{no=1}
HeroNode{no=14}
HeroNode{no=6}思路:
树结构的实际应用
堆排序
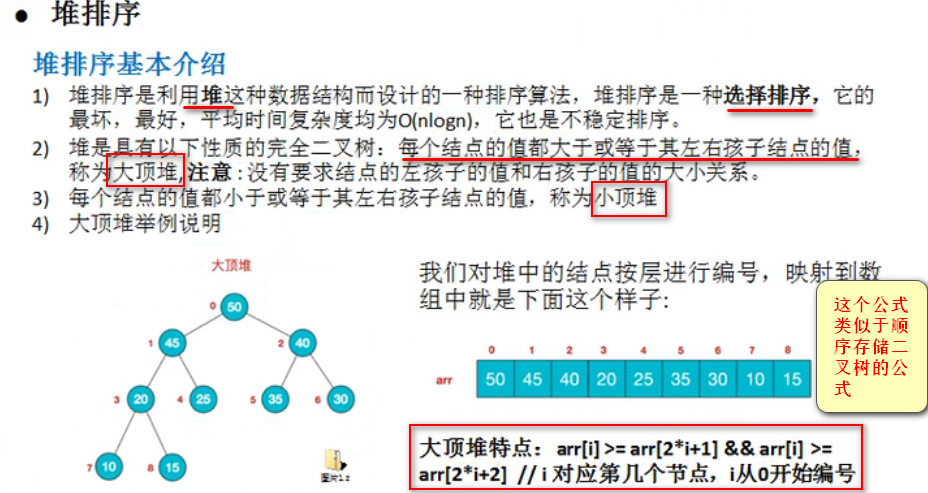
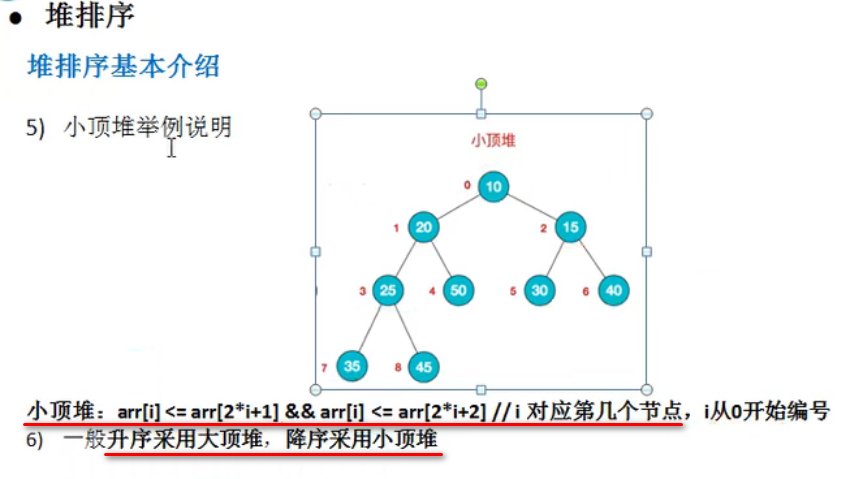
堆排序基本思想
1.将待排序列构造成一个大顶堆
2.此时整个序列的最大值就是堆顶的根节点
3.将其以末尾的元素进行交换,此时末尾就是最大值。
4.然后将剩余n-1各元素重新构造成一个堆,这样就会得到n个元素的最次小值,如此反复执行,便能得到一个有序序列。
可以看到,在构建大顶堆的过程中,元素的个数逐渐减少,最后就得到一个有序序列了
例子,如原始数组如{4,6,8,5,9},按照堆排序从小到大排序,(一般升序采用大顶堆,降序采用小顶堆)
1.
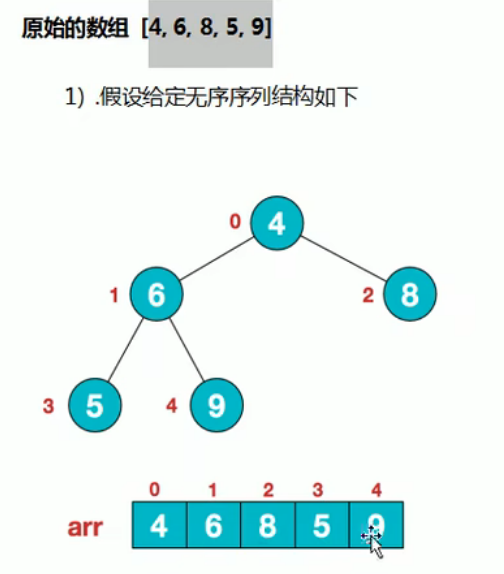
2.
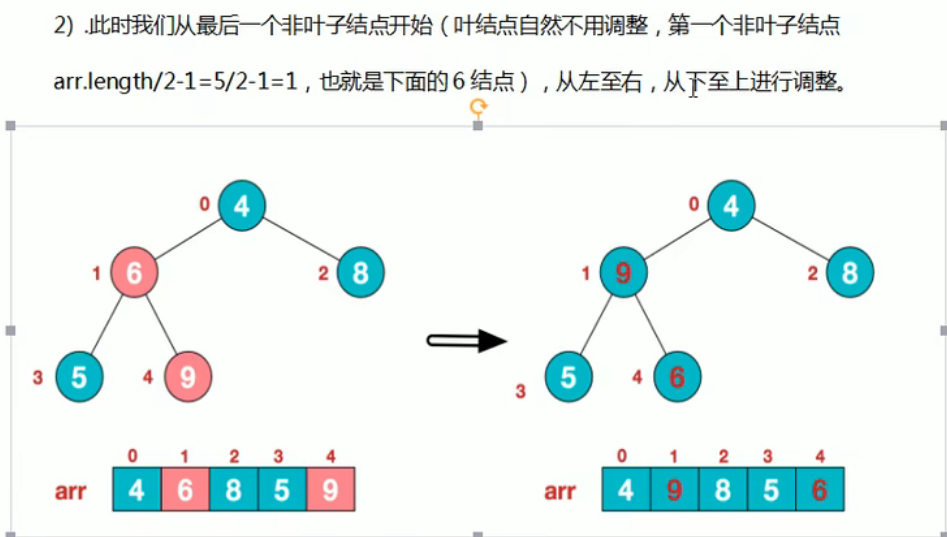
3.
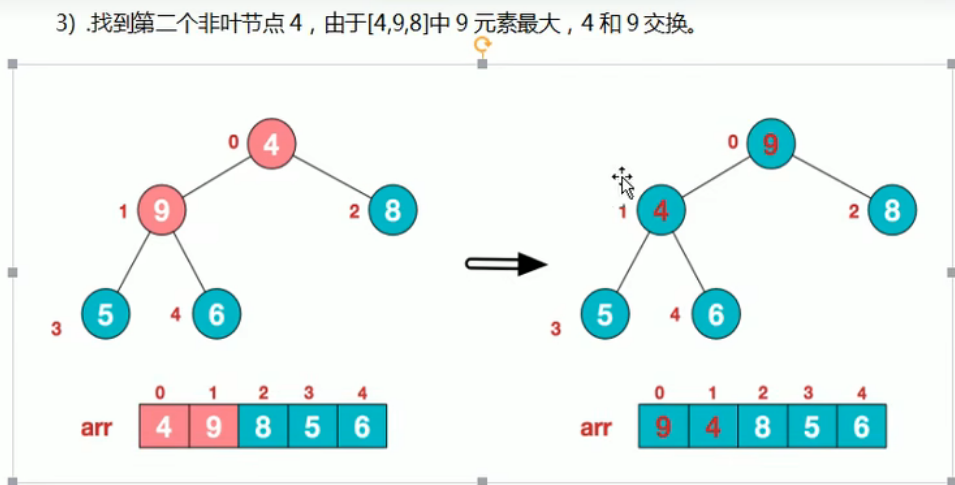
4.
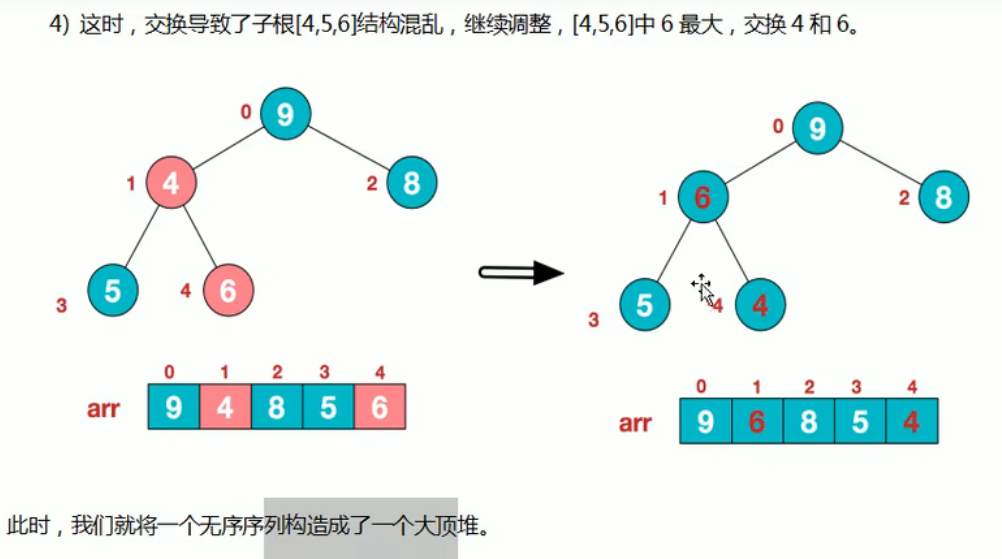
步骤二:将堆顶元素和末尾元素进行交换,使末尾元素最大,然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素,如此反复交换,重建,交换
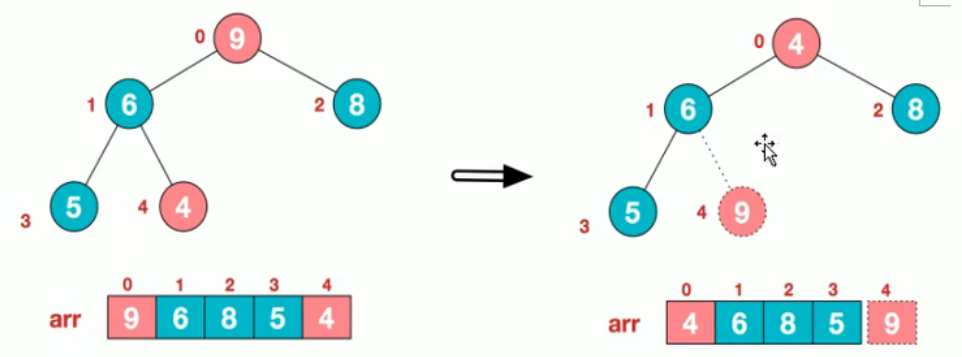
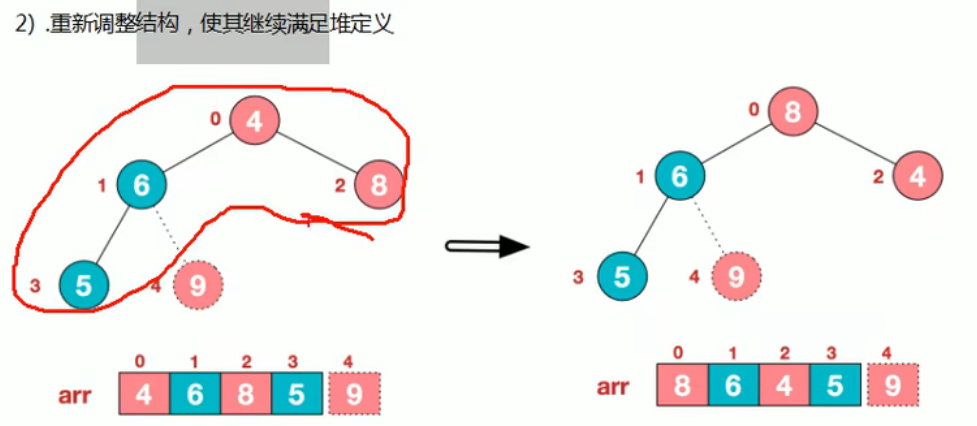
3.
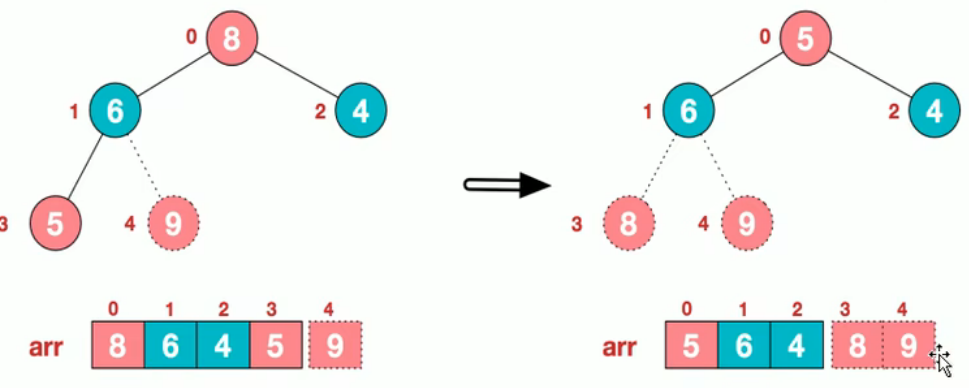
简单总结:
1.将无序序列构建成一个堆,根据升序降序需求,选择大顶堆或者小顶堆。
2.将堆顶元素与末尾元素交换,将最大的元素沉到数组末端。
3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
堆排序的代码实现未完成,后续学习!
public class HeapSort {
public static void main(String[] args) {
int arr[] = {4, 6, 8, 5, 9};
heapSort(arr);
}
public static void heapSort(int arr[]) {
int temp=0;
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustheap(arr, i, arr.length);
}
for (int j = arr.length - 1; j > 0; j--) {
temp=arr[j];
arr[j]=arr[0];
arr[0]=temp;
adjustheap(arr,0,j);
}
System.out.println("数组="+Arrays.toString(arr));
}
public static void adjustheap(int arr[], int i, int length) {
int temp = arr[i];
//int k = i * 2 + 1 k是i节点的左子节点
for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {
if (k + 1 < length && arr[k] < arr[k + 1]) {
//左子节点小于右子节点,k指向右子节点
k++;
}
if (arr[k] > temp) {
arr[i] = arr[k];
i = k;
} else {
break;
}
//当for循环结束,已经将以i为父节点的树的最大值,放在最顶(局部)
arr[i] = temp;
}
}
}
输出:符合预期
数组=[4, 5, 6, 8, 9]速率测试:
public static void main(String[] args) {
int[] arr = new int[80000];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * 80000);
}
Date date1=new Date();
heapSort(arr);
Date date2=new Date();
System.out.println("堆排序耗时:"+(date2.getTime()-date1.getTime()));
System.out.println("排序结果:"+Arrays.toString(arr));
}
输出:
堆排序耗时:12
排序结果:[0, 1, 1, ...]速率是非常的快!!!
霍夫曼树
基本介绍:
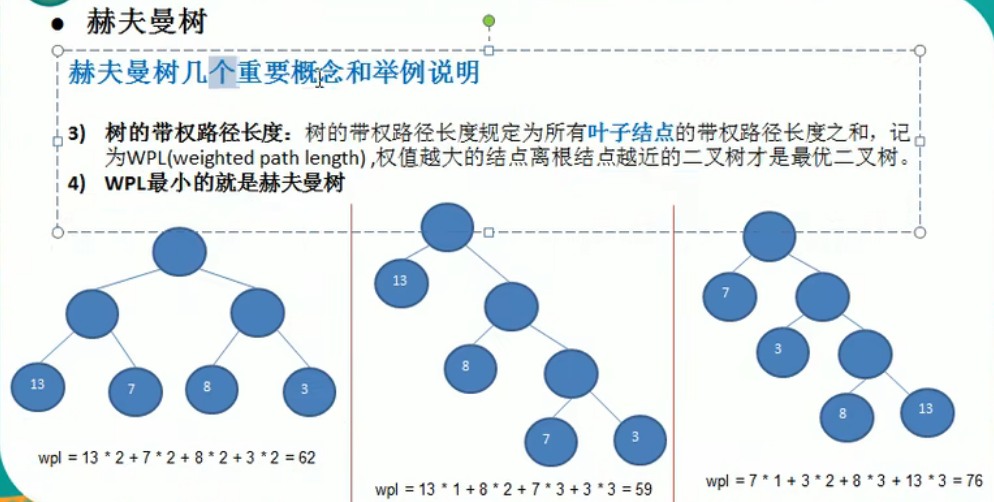
1.给定n个权值作为n个叶子节点,构造一颗二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称之为哈夫曼树
2.霍夫曼树是带权路径长度最短的树,权值较大的节点离根较近。

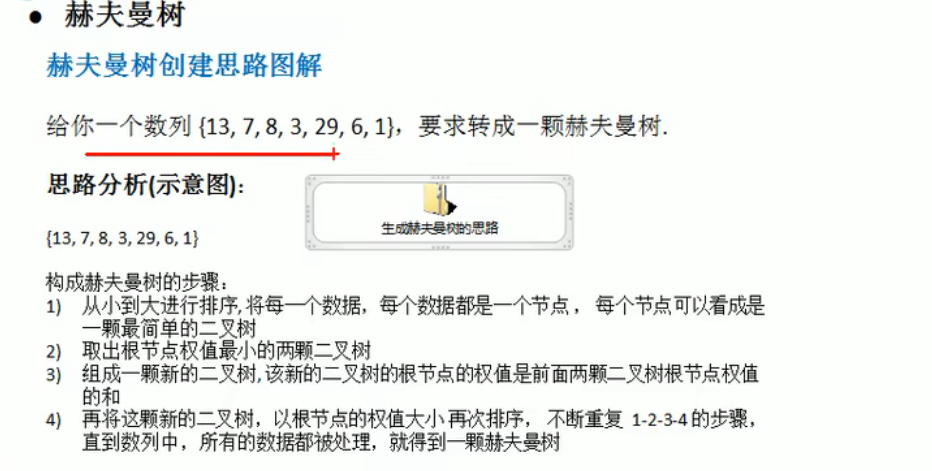
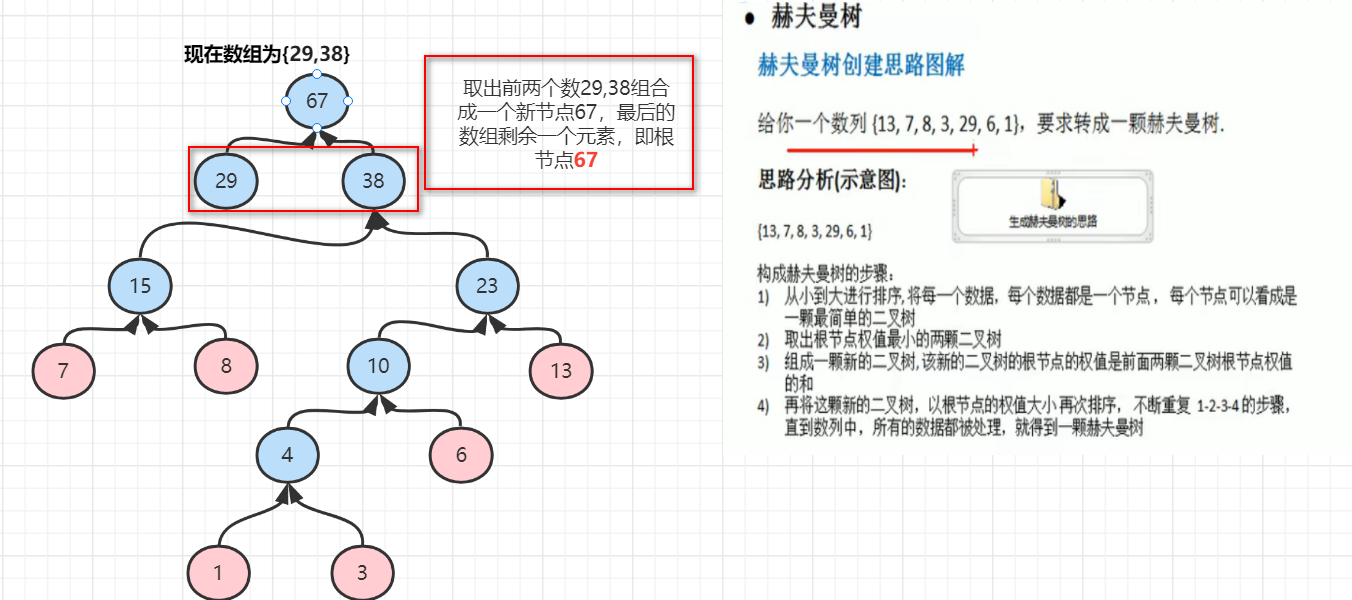
组成一个赫夫曼树步骤:
1.
原数组排序为{1,3,6,7,8,13,29}

2.


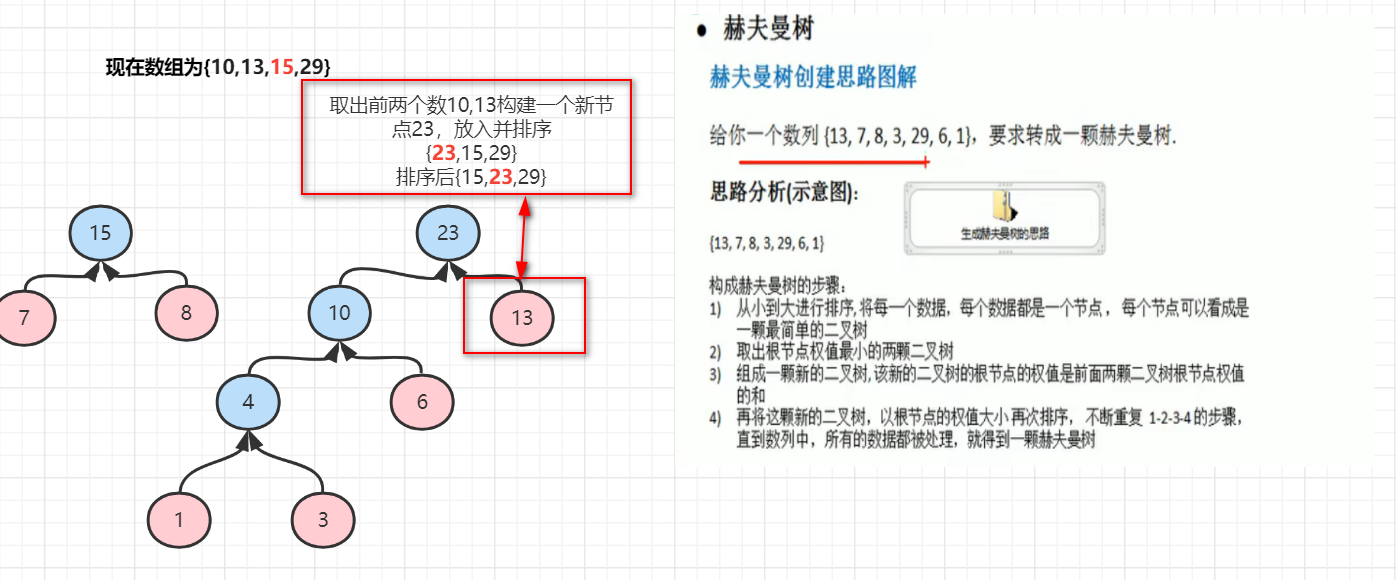
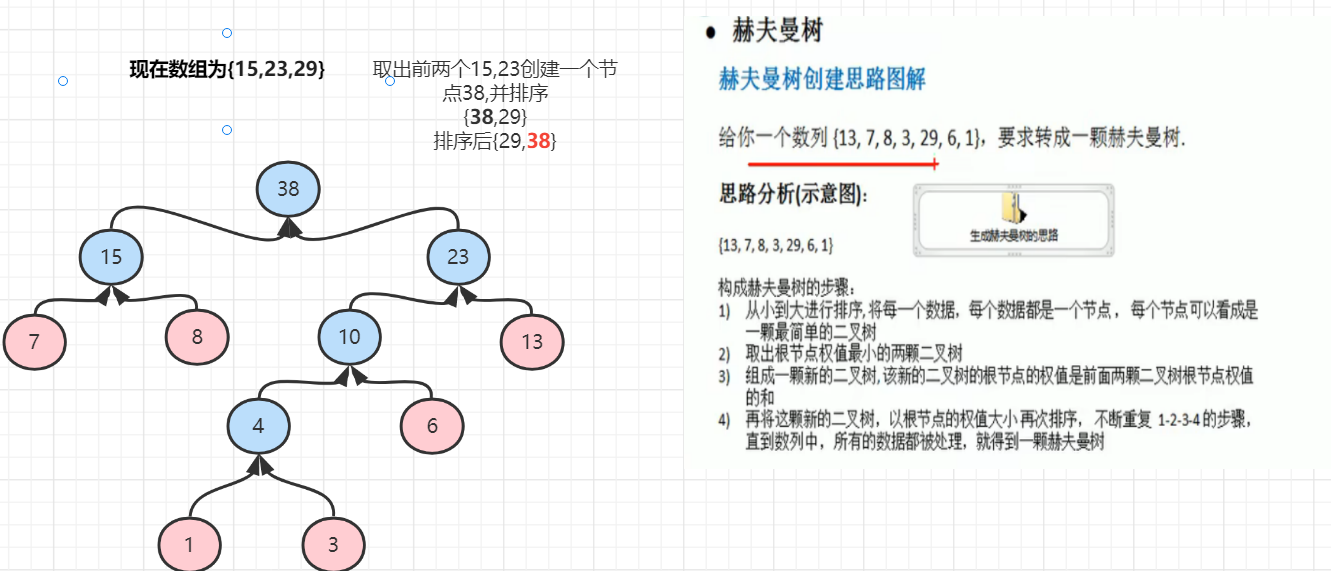
3.完成霍夫曼树
代码实现
package cn.com.tree;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
/**
* 创建霍夫曼树
*/
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = {13, 7, 8, 3, 29, 6, 1};
System.out.println("原数组:"+ Arrays.toString(arr));
Node root=createHuffmnTree(arr);
System.out.println("前序遍历霍夫曼树:");
root.preOrder();
}
public static Node createHuffmnTree(int arr[]) {
//1.遍历数组,每个元素创建一个node节点,并放入到list中
List<Node> nodes = new ArrayList<>();
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
//从小到大排序,每次都得排序
Collections.sort(nodes);
System.out.println("排序结果:"+nodes);
//1.取出权值最小的节点
Node leftNode = nodes.get(0);
//2.取出权值次小的节点
Node rightNode = nodes.get(1);
//3.创建一个新的节点,值是两个最小节点的和
Node parent = new Node(leftNode.getValue() + rightNode.getValue());
parent.setLeft(leftNode);
parent.setRight(rightNode);
//4.集合中删除两个已经处理过的节点
nodes.remove(leftNode);
nodes.remove(rightNode);
//5.将新节点放入
nodes.add(parent);
}
System.out.println("最后集合剩余:"+nodes);
return nodes.get(0);
}
}
/**
* 创建节点类
* 方便排序,对象实现collection集合排序
*/
class Node implements Comparable<Node> {
//节点值
private int value;
//左节点
private Node left;
//右节点
private Node right;
/**
* 前序遍历
*/
public void preOrder() {
System.out.print(this.getValue()+" ");
if (this.getLeft() != null) {
this.getLeft().preOrder();
}
if (this.getRight() != null) {
this.getRight().preOrder();
}
}
public Node(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
//node节点从小到大排序
@Override
public int compareTo(Node o) {
return this.value - o.getValue();
}
@Override
public String toString() {
return value+" ";
}
}
测试输出:
原数组:[13, 7, 8, 3, 29, 6, 1]
排序结果:[1 , 3 , 6 , 7 , 8 , 13 , 29 ]
排序结果:[4 , 6 , 7 , 8 , 13 , 29 ]
排序结果:[7 , 8 , 10 , 13 , 29 ]
排序结果:[10 , 13 , 15 , 29 ]
排序结果:[15 , 23 , 29 ]
排序结果:[29 , 38 ]
最后集合剩余:[67 ]
前序遍历霍夫曼树:
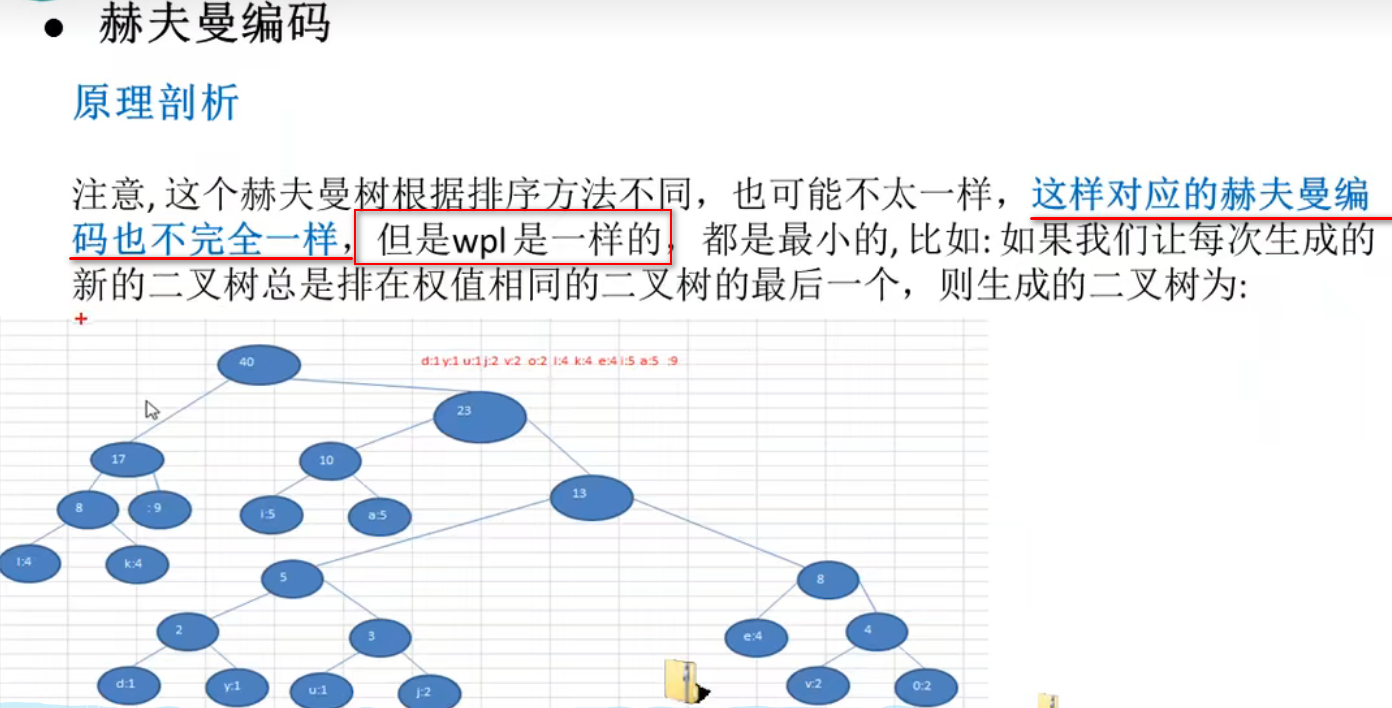
67 29 38 15 7 8 23 10 4 1 3 6 13霍夫曼编码
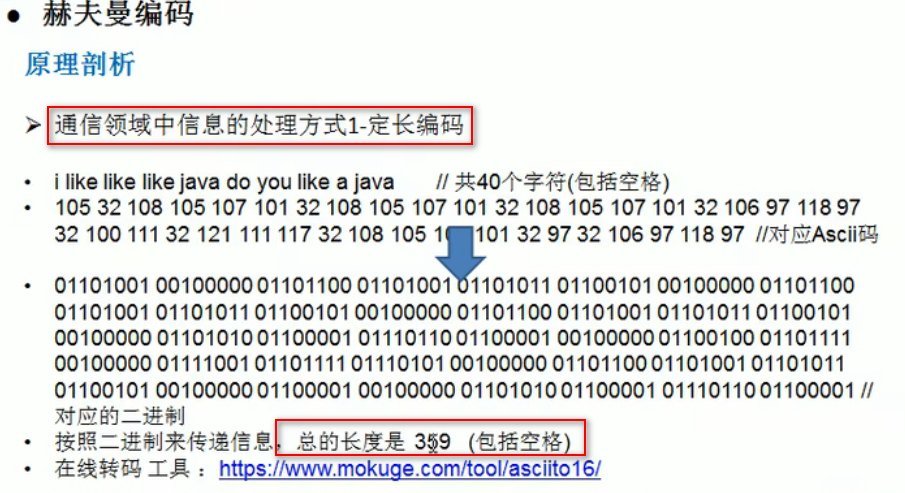
基本介绍:
1.赫夫曼编码是一种编码方式,属于一种程序算法
2.赫夫曼编码是赫夫曼树在电讯通信中的经典应用之一
3.赫夫曼编码被广泛用于数据文件压缩,其压缩率通常在20%-90%之间
4.赫夫曼码是可变字长编码(VLC)的一种,于1952年提出的一种编码方式,称为最佳编码

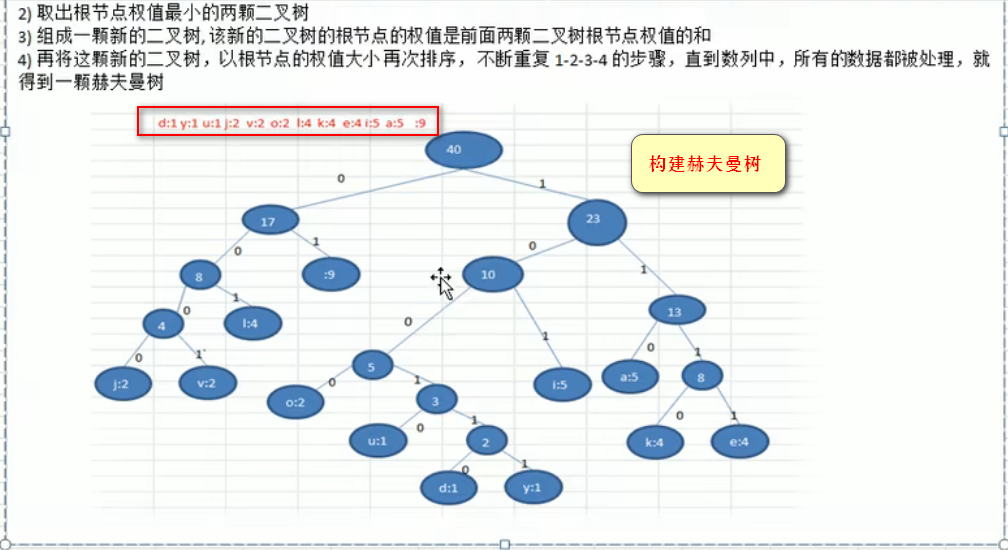
构造赫夫曼树
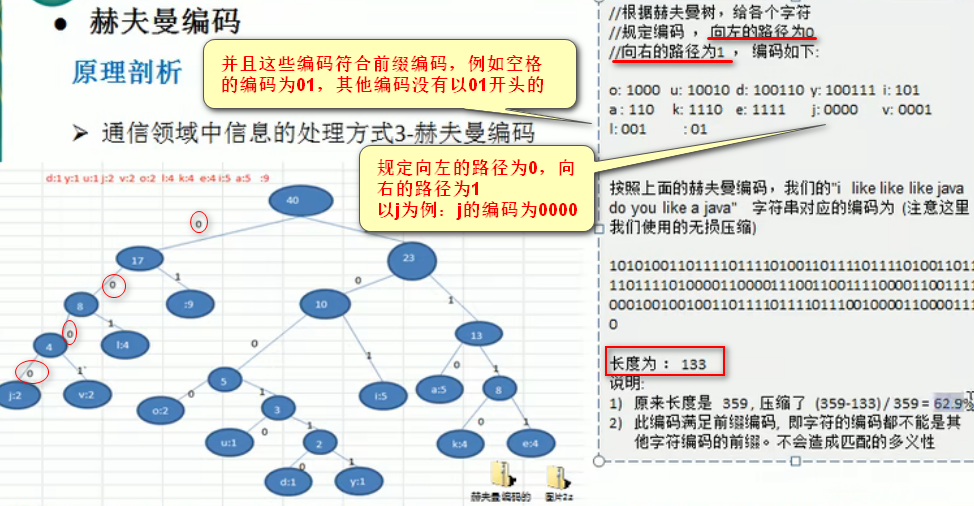
赫夫曼编码是无损压缩,恢复后不会造成数据的不同!
霍夫曼树用于数据压缩

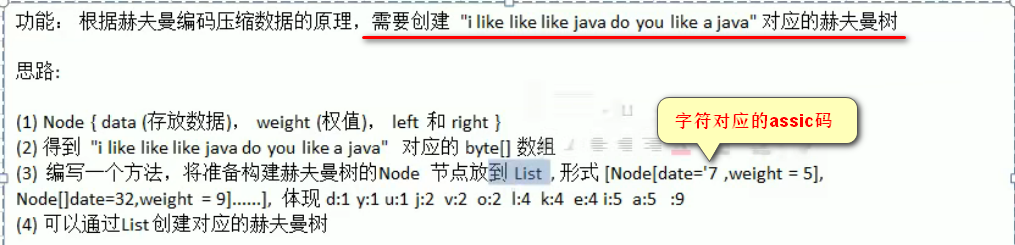
1.生成赫夫曼树
public class HuffmanCode {
public static void main(String[] args) {
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println("原字符串长度:" + content.length() + " 转换后byte数组长度:" + contentBytes.length);
List<Node> nodes = getNodes(contentBytes);
System.out.println("nodes=" + nodes);
System.out.println("======创建霍夫曼树");
Node huffmanTreeRoot = createHuffmanTree(nodes);
System.out.println("前序遍历:");
huffmanTreeRoot.preOrder();
}
/**
* 将字符串byte数组转换为对应的node节点集合
*
* @param bytes
* @return
*/
public static List<Node> getNodes(byte[] bytes) {
List<Node> nodes = new ArrayList<>();
//key=字符,value=字符出现的次数
Map<Byte, Integer> counts = new HashMap<>();
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) {
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
/**
* 穿件霍夫曼树
*
* @param nodes
* @return 根节点
*/
public static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
//每次都从小到大排序下
Collections.sort(nodes);
//最小的节点
Node leftNode = nodes.get(0);
//次小的节点
Node rightNode = nodes.get(1);
//注意:所有的元素都保存在叶子节点上,根节点上并不存储元素,只存储两个叶子节点的权值和
Node parent = new Node(null, leftNode.weight + rightNode.weight);
//父节点左右节点赋值
parent.left = leftNode;
parent.right = rightNode;
//原集合中删除左右节点
nodes.remove(leftNode);
nodes.remove(rightNode);
//把父节点加进去
nodes.add(parent);
}
return nodes.get(0);
}
}
class Node implements Comparable<Node> {
//存放数据本身,比如'a'对应的assic码值为97等
Byte data;
//权值,字符出现的次数
int weight;
//左节点
Node left;
//右节点
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
public Node(Node left, Node right) {
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
/**
* 从小到大排序
*/
@Override
public int compareTo(Node o) {
return this.weight - o.weight;
}
/**
* 前序遍历
*/
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
输出:
原字符串长度:40 转换后byte数组长度:40
nodes=[Node{data=32, weight=9}, Node{data=97, weight=5}, Node{data=100, weight=1}, Node{data=101, weight=4}, Node{data=117, weight=1}, Node{data=118, weight=2}, Node{data=105, weight=5}, Node{data=121, weight=1}, Node{data=106, weight=2}, Node{data=107, weight=4}, Node{data=108, weight=4}, Node{data=111, weight=2}]
======创建霍夫曼树
前序遍历:
Node{data=null, weight=40}
Node{data=null, weight=17}
Node{data=null, weight=8}
Node{data=108, weight=4}
Node{data=null, weight=4}
Node{data=106, weight=2}
Node{data=111, weight=2}
Node{data=32, weight=9}
Node{data=null, weight=23}
Node{data=null, weight=10}
Node{data=97, weight=5}
Node{data=105, weight=5}
Node{data=null, weight=13}
Node{data=null, weight=5}
Node{data=null, weight=2}
Node{data=100, weight=1}
Node{data=117, weight=1}
Node{data=null, weight=3}
Node{data=121, weight=1}
Node{data=118, weight=2}
Node{data=null, weight=8}
Node{data=101, weight=4}
Node{data=107, weight=4}2.生成赫夫曼编码

package cn.com.Huffman;
import java.util.*;
import java.util.stream.Stream;
public class HuffmanCode {
public static void main(String[] args) {
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println("原字符串长度:" + content.length() + " 转换后byte数组长度:" + contentBytes.length);
List<Node> nodes = getNodes(contentBytes);
System.out.println("nodes=" + nodes);
System.out.println("======创建霍夫曼树");
Node huffmanTreeRoot = createHuffmanTree(nodes);
System.out.println("前序遍历:");
huffmanTreeRoot.preOrder();
System.out.println("获取赫夫曼编码表================");
getCodes(huffmanTreeRoot);
System.out.println(huffmanCodes);
}
//创建map,key为字符对应的assic码值,value为对应的路径
static Map<Byte, String> huffmanCodes = new HashMap<>();
/**
* 重点!!!!!!
*
* @param node
* @return 赫夫曼编码表
*/
private static Map<Byte, String> getCodes(Node node) {
if (node == null) {
return null;
} else {
getCodes(node, "", new StringBuilder());
}
return huffmanCodes;
}
/**
* 重点!!!!!!
* 获取赫夫曼编码表
* 重点1:赫夫曼编码的内容,如i,l,i等字符对应的assic码都保存在叶子节点上,根节点上没有对应的data(字符对应的asscic值),只有weight(两个叶子节点的权值和)
* 重点2:赫夫曼树向左为code=0,向右code=1
*
* @param node 节点
* @param code 赫夫曼树向左为code=0,向右code=1
* @param sb 路径拼接对象
*/
private static void getCodes(Node node, String code, StringBuilder sb) {
StringBuilder stringBuilder1 = new StringBuilder(sb);
//拼接路径:赫夫曼树向左为code=0,向右code=1
stringBuilder1.append(code);
if (node != null) {
if (node.data == null) {
//该节点为非叶子节点,字符对应的assic编码会存储在也在节点上,根节点上没有对应的data(字符对应的asscic值),只有weight(两个叶子节点的权值和)
//左遍历
getCodes(node.left, "0", stringBuilder1);
//右遍历
getCodes(node.right, "1", stringBuilder1);
} else {
//叶子节点,存储的是字符对应的assic码
huffmanCodes.put(node.data, stringBuilder1.toString());
}
}
}
/**
* 将字符串byte数组转换为对应的node节点集合
*
* @param bytes
* @return
*/
public static List<Node> getNodes(byte[] bytes) {
List<Node> nodes = new ArrayList<>();
//key=字符,value=字符出现的次数
Map<Byte, Integer> counts = new HashMap<>();
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) {
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
for (Map.Entry<Byte, Integer> entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
/**
* 穿件霍夫曼树
*
* @param nodes
* @return 根节点
*/
public static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
//每次都从小到大排序下
Collections.sort(nodes);
//最小的节点
Node leftNode = nodes.get(0);
//次小的节点
Node rightNode = nodes.get(1);
//注意:所有的元素都保存在叶子节点上,根节点上并不存储元素,只存储两个叶子节点的权值和
Node parent = new Node(null, leftNode.weight + rightNode.weight);
//父节点左右节点赋值
parent.left = leftNode;
parent.right = rightNode;
//原集合中删除左右节点
nodes.remove(leftNode);
nodes.remove(rightNode);
//把父节点加进去
nodes.add(parent);
}
return nodes.get(0);
}
}
class Node implements Comparable<Node> {
//存放数据本身,比如'a'对应的assic码值为97等
Byte data;
//权值,字符出现的次数
int weight;
//左节点
Node left;
//右节点
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
public Node(Node left, Node right) {
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
/**
* 从小到大排序
*/
@Override
public int compareTo(Node o) {
return this.weight - o.weight;
}
/**
* 前序遍历
*/
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
输出:
.......
获取赫夫曼编码表================
{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}3.按照赫夫曼编码字典进行编码,获取编码后传输的对应byte数组
/**
* 重点!!!!!!!
* 将字符串按照赫夫曼编码字典进行编码后,获取对应的byte数组
*
* @param bytes 原始字符串字符对应的assic码byte数组
* @param huffmanCodes 赫夫曼编码字典表:map key=字符对应的assic码,value=对应的赫夫曼树路径
* @return 编码后的赫夫曼编码byte数组
*/
public static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
StringBuilder sb = new StringBuilder();
for (byte b : bytes) {
//获取赫夫曼编码对应的路径拼接:类似于10001101010....
sb.append(huffmanCodes.get(b));
}
System.out.println("赫夫曼路径拼接结果:" + sb.toString());
//创建的byte数组长度
int len;
if (sb.length() % 8 == 0) {
//刚好是byte 8位的倍数
len = sb.length() / 8;
} else {
//在原始基础上+1
len = sb.length() / 8 + 1;
}
byte[] huffmanCodeBytes = new byte[len];
int index = 0;
for (int i = 0; i < sb.length(); i += 8) {
String strByte;
if (i + 8 > sb.length()) {
//最后几位,不够8位
strByte = sb.substring(i);
} else {
//截取8为的二进制
strByte = sb.substring(i, i + 8);
}
//将二进制的string转byte
huffmanCodeBytes[index++] = (byte) Integer.parseInt(strByte, 2);
}
return huffmanCodeBytes;
}
测试:
public static void main(String[] args) {
String content = "i like like like java do you like a java";
byte[] contentBytes = content.getBytes();
System.out.println("原字符串长度:" + content.length() + " 转换后byte数组长度:" + contentBytes.length);
List<Node> nodes = getNodes(contentBytes);
System.out.println("nodes=" + nodes);
System.out.println("======创建霍夫曼树");
Node huffmanTreeRoot = createHuffmanTree(nodes);
System.out.println("前序遍历:");
huffmanTreeRoot.preOrder();
System.out.println("获取赫夫曼编码表================");
getCodes(huffmanTreeRoot);
System.out.println(huffmanCodes);
//重点:测试
System.out.println("赫夫曼编码转换为对应byte数组================");
byte[] zip = zip(contentBytes, huffmanCodes);
System.out.println("原字符串长度:" + contentBytes.length + " 转换后byte数组长度:" + zip.length);
System.out.println("转换后的byte数组长度:"+zip.length+" 压缩比为:"+(double)(contentBytes.length-zip.length)/contentBytes.length);
System.out.println("转换后的赫夫曼byte数组:"+Arrays.toString(zip));
}
输出:
E:\work\jdk\bin\java.exe "-javaagent:E:\work\idea\IntelliJ IDEA 2020.1\lib\idea_rt.jar=61626:E:\work\idea\IntelliJ IDEA 2020.1\bin" -Dfile.encoding=UTF-8 -classpath E:\work\jdk\jre\lib\charsets.jar;E:\work\jdk\jre\lib\deploy.jar;E:\work\jdk\jre\lib\ext\access-bridge-64.jar;E:\work\jdk\jre\lib\ext\cldrdata.jar;E:\work\jdk\jre\lib\ext\dnsns.jar;E:\work\jdk\jre\lib\ext\jaccess.jar;E:\work\jdk\jre\lib\ext\jfxrt.jar;E:\work\jdk\jre\lib\ext\localedata.jar;E:\work\jdk\jre\lib\ext\nashorn.jar;E:\work\jdk\jre\lib\ext\sunec.jar;E:\work\jdk\jre\lib\ext\sunjce_provider.jar;E:\work\jdk\jre\lib\ext\sunmscapi.jar;E:\work\jdk\jre\lib\ext\sunpkcs11.jar;E:\work\jdk\jre\lib\ext\zipfs.jar;E:\work\jdk\jre\lib\javaws.jar;E:\work\jdk\jre\lib\jce.jar;E:\work\jdk\jre\lib\jfr.jar;E:\work\jdk\jre\lib\jfxswt.jar;E:\work\jdk\jre\lib\jsse.jar;E:\work\jdk\jre\lib\management-agent.jar;E:\work\jdk\jre\lib\plugin.jar;E:\work\jdk\jre\lib\resources.jar;E:\work\jdk\jre\lib\rt.jar;E:\work\idea\idea_workspace\DataStructures\target\classes cn.com.Huffman.HuffmanCode
原字符串长度:40 转换后byte数组长度:40
nodes=[Node{data=32, weight=9}, Node{data=97, weight=5}, Node{data=100, weight=1}, Node{data=101, weight=4}, Node{data=117, weight=1}, Node{data=118, weight=2}, Node{data=105, weight=5}, Node{data=121, weight=1}, Node{data=106, weight=2}, Node{data=107, weight=4}, Node{data=108, weight=4}, Node{data=111, weight=2}]
======创建霍夫曼树
前序遍历:
Node{data=null, weight=40}
Node{data=null, weight=17}
Node{data=null, weight=8}
Node{data=108, weight=4}
Node{data=null, weight=4}
Node{data=106, weight=2}
Node{data=111, weight=2}
Node{data=32, weight=9}
Node{data=null, weight=23}
Node{data=null, weight=10}
Node{data=97, weight=5}
Node{data=105, weight=5}
Node{data=null, weight=13}
Node{data=null, weight=5}
Node{data=null, weight=2}
Node{data=100, weight=1}
Node{data=117, weight=1}
Node{data=null, weight=3}
Node{data=121, weight=1}
Node{data=118, weight=2}
Node{data=null, weight=8}
Node{data=101, weight=4}
Node{data=107, weight=4}
获取赫夫曼编码表================
{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
赫夫曼编码转换为对应byte数组================
赫夫曼路径拼接结果:1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
原字符串长度:40 转换后byte数组长度:17
转换后的byte数组长度:17 压缩比为:0.575
转换后的赫夫曼byte数组:[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]发现原始字符串长度传输需要40个字节,但是赫夫曼压缩后传输只需要17个字节,压缩比达到了%57.5,相当可以了!
赫夫曼树数据解压

前提知识,代码里会用到将byte数组转二进制的代码:
1.原码:是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值
2.反码:正数的反码还是等于原码;负数的反码就是它的原码除符号位外,按位取反
3.补码:正数的补码等于它的原码;负数的补码等于反码+1具体可以参考:https://blog.csdn.net/qq_44543508/article/details/121624103
private static void byteToBitString(byte b) {
int temp = b;
/*
该方法返回的是二进制的补码
1.原码:是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值
2.反码:正数的反码还是等于原码;负数的反码就是它的原码除符号位外,按位取反
3.补码:正数的补码等于它的原码;负数的补码等于反码+1
*/
String str = Integer.toBinaryString(temp);
System.out.println("str:" + str+" 长度:"+str.length());
}
测试:
byteToBitString((byte) 1);
byteToBitString((byte) -1);
输出:
str:1 长度:1
str:11111111111111111111111111111111 长度:32
结论:
发现正数1的输出为:1(自己本身)
负数-1的输出为:11111111111111111111111111111111
-1的原码是:1000 0001
-1的反码是:1111 1110(负数的反码就是它的原码除符号位外,按位取反)
-1的补码是:1111 1111(负数的补码等于反码+1)
Integer.toBinaryString(temp);返回的是二进制的补码
这里有个问题,正数返回的不够8位的二进制:
如Integer.toBinaryString(1) 返回1
Integer.toBinaryString(3) 返回11
Integer.toBinaryString(5) 返回101
负数的返回是32位的:
byteToBitString((byte) -5) 返回:11111111111111111111111111111011 (补码返回)
想要返回一个8位的,就会涉及一个负数截取,正数补位的动作
这么做:
private static void byteToBitString(byte b) {
int temp = b;
/*
该方法返回的是二进制的补码
1.原码:是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值
2.反码:正数的反码还是等于原码;负数的反码就是它的原码除符号位外,按位取反
3.补码:正数的补码等于它的原码;负数的补码等于反码+1
*/
temp |=256;
String str = Integer.toBinaryString(temp);
System.out.println("str:" + str+" 长度:"+str.length());
}
正数按位或
temp |=256;
256:1 0000 0000
1 : 1
按位或:1 0000 0001
负数按位或
256:1 0000 0000
-1 : 1000 0001
按位或:1 1000 0001
这时,temp的长度都超过了8位,就可以进行截取了!
测试:
byteToBitString((byte) 1);
byteToBitString((byte) -1);
输出:
str:100000001 长度:9
str:11111111111111111111111111111111 长度:32解压缩代码:
/**
* 将一个byte转成一个二进制的字符串
* 原始传来的二进制数组为[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
* 将其转为对应的二进制返回
*
* @param b 传入的byte
* @param flag 标志位,表示是否需要补位
* @return 按补码返回对应的二进制字符串
*/
private static String byteToBitString(boolean flag, byte b) {
int temp = b;
/*
该方法返回的是二进制的补码
1.原码:是最简单的机器数表示法,用最高位表示符号位,其他位存放该数的二进制的绝对值
2.反码:正数的反码还是等于原码;负数的反码就是它的原码除符号位外,按位取反
3.补码:正数的补码等于它的原码;负数的补码等于反码+1
*/
if (flag) {
/**
* 这里注意:在当初压缩时,最后一个byte,可能不是8位,如28==>11100,用下述Integer.toBinaryString(temp)转换时,会进行补0,为1 0001 1100
* 这样拼接出来的二进制字符串可能会有问题:如原始为:之前11100 ==> 之前0001 1100
* 后续处理逻辑是:逐个截取二进制字符串,在字典中找,这多出几位可能会有问题!
*/
temp |= 256;
}
String str = Integer.toBinaryString(temp);
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
/**
* @param huffmanCodes
* @param hubBytes
* @return
*/
private static byte[] decode(Map<Byte, String> huffmanCodes, byte[] hubBytes) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < hubBytes.length; i++) {
byte b = hubBytes[i];
boolean flag = (i == hubBytes.length - 1);
//最后一位不需要补位,直接返回即可!
sb.append(byteToBitString(!flag, b));
}
System.out.println("转为二进制:" + sb.toString());
//将字典的key和value调换,因为解码是通过二进制字符串找对应的assi码
Map<String, Byte> map = new HashMap<>();
for (Byte key : huffmanCodes.keySet()) {
map.put(huffmanCodes.get(key), key);
}
System.out.println("原始的压缩字典值:" + huffmanCodes);
System.out.println("用于解压的字典值:" + map);
List<Byte> list = new ArrayList<>();
for (int i = 0; i < sb.length(); ) {
int cout = 0;
while (true) {
String str = sb.substring(i, i + cout);
if (map.get(str) != null) {
list.add(map.get(str));
System.out.println(str + ":" + map.get(str));
break;
}
cout++;
}
i += cout;
}
System.out.println(list.size());
byte[] bytes = new byte[list.size()];
for (int i = 0; i < list.size(); i++) {
bytes[i] = list.get(i);
}
return bytes;
}
测试:
System.out.println("二进制转换===============");
byte[] decode = decode(huffmanCodes, zip);
System.out.println("解码后的报文:"+new String(decode));
输出:
二进制转换===============
转为二进制:1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
原始的压缩字典值:{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
用于解压的字典值:{000=108, 01=32, 100=97, 101=105, 11010=121, 0011=111, 1111=107, 11001=117, 1110=101, 11000=100, 11011=118, 0010=106}
i like like like java do you like a java
和预期一样,解码成功 赫夫曼编码的最佳实现---文件压缩

压缩代码示例:
/**
* 压缩文件
*
* @param srcFile 源文件路径
* @param dstFile 目标文件路径
*/
private static void zipFile(String srcFile, String dstFile) {
//创建输出流
OutputStream ops = null;
ObjectOutputStream oos = null;
//创建文件输入流
FileInputStream fis = null;
try {
//创建文件输入流
fis = new FileInputStream(srcFile);
byte[] b = new byte[fis.available()];
//读取文件
fis.read(b);
//重点:压缩文件
byte[] zip = huffmanZip(b);
System.out.println("源文件大小:" + b.length + " 压缩后的大小:" + zip.length + " 压缩比:" + (double) (b.length - zip.length) / b.length);
//创建文件的输出流,存放压缩文件
ops = new FileOutputStream(dstFile);
//创建一个和文件输出流关联的ObjectOutputStream
oos = new ObjectOutputStream(ops);
//把赫夫曼编码后的字节数组写入压缩文件
oos.writeObject(zip);
//把赫夫曼编码写入到压缩文件
oos.writeObject(huffmanCodes);
} catch (Exception e) {
e.printStackTrace();
} finally {
try {
fis.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
/**
* 获取编码后的byte数组
* 方法中的代码在上面有,直接搜索即可,没有复制过来,要不太多了!
* @param contentBytes 原始的的byte数组
* @return
*/
private static byte[] huffmanZip(byte[] contentBytes) {
//原始的byte转node节点集合
List<Node> nodes = getNodes(contentBytes);
//创建霍夫曼树
Node huffmanTreeRoot = createHuffmanTree(nodes);
//获取霍夫曼编码表
huffmanCodes = getCodes(huffmanTreeRoot);
//根据霍夫曼编码表压缩文件
byte[] zip = zip(contentBytes, huffmanCodes);
return zip;
}
测试
public static void main(String[] args) {
zipFile("C:\\Users\\Administrator\\Desktop\\图片\\测试压缩.png", "C:\\Users\\Administrator\\Desktop\\图片\\压缩后.zip");
}
输出:
赫夫曼路径拼接结果:100101011101....
源文件大小:16024 压缩后的大小:14012 压缩比:0.1255616575137294
赫夫曼编码的最佳实现---文件解压

/**
* 解压文件
*
* @param zipFile 解压源文件路径
* @param dstFile 解压后文件存储位置
*/
private static void unZipFile(String zipFile, String dstFile) {
//定义文件输入流
InputStream is = null;
//定义对象输入流
ObjectInputStream ois = null;
//定义文件输出流
OutputStream os = null;
try {
is = new FileInputStream(zipFile);
//创建对象输入流
ois = new ObjectInputStream(is);
//读取byte数组
byte[] huffmanBytes = (byte[]) ois.readObject();
//读取赫夫曼编码
Map<Byte, String> codes = (Map<Byte, String>) ois.readObject();
//解码
byte[] bytes = decode(codes, huffmanBytes);
os = new FileOutputStream(dstFile);
os.write(bytes);
} catch (Exception e) {
e.printStackTrace();
}finally {
try {
os.close();
ois.close();
is.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
测试:
unZipFile("C:\\Users\\Administrator\\Desktop\\图片\\压缩后.zip","C:\\Users\\Administrator\\Desktop\\图片\\解压后.png");
结论:完美解压,解压后的大小一样,没有任何损失!
总结:








