PLA

PLA：Perceptron Learning Algorithm
PLA的任务就是找到将数据集划分为两个区域的线。
基本模型

也可以叫linear classifiers

注意：上标表示第几个样本，下标表示这个样本的第几个特征

PLA算法流程：
输入：训练数据集{(X1,Y1),(X2,Y2),...,(XN,YN)}
输出：W
(1)选取初值W0
(2)从训练集中选取样本(Xi,Yi)
(3)更新。如果Yi(WtXi)≤0, 则Wt+1=Wt+ηYiXi
(4)转至(2),直至训练集中的所有样本被完全正确分类。

具体更新流程：

用法
假设现在我们通过PLA算法已经求得了一个模型。现在需要去预测一个不知道标签的样本的标签是多少？
我们把这个样本的特征X带入到h(X)中，h(X)就会等于+1或者-1(这个模型判断的这个样本最有可能属于哪个类别)，我们就预测出来这个样本的标签了。

当W（T）与W（f）越来越接近时，两个的内项积越来越大，也有可能是长度变大的原因，因此要考虑以下因素：

主要靠红色那一项增长，y（n）为正负1，平方之后为1.
其中yWx<0表示分割的区域内有不符合的点，因此乘积为负。

经过T此矫正，可得到以下结果：

表示两个正规化向量内积大小表示角度大小。

PLA优劣
好处：
简单，快速。100维和二维是一样的，只是时间多五十倍。
坏处：
假设数据是线性可分的，且计算需要用的W（f），这个是未知的。

关于noise
数据集f中有wrong date（noise），且D中也有可能包含noise

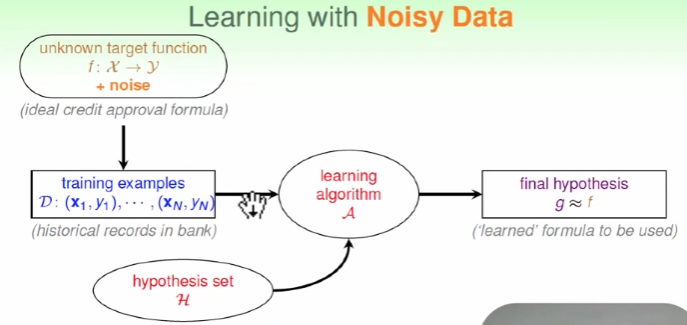
因此引入Noise Tolerant，g为犯错最少的线，但这是NP-hard问题。

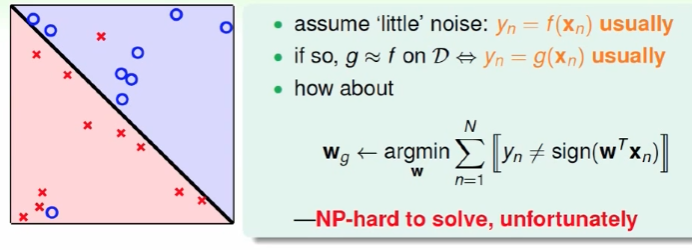
可以用口袋算法：

跑足够多次返回最佳答案，若线性可分，用口袋算法比PLA更费时，口袋需要把所有数据跑一遍，PLA找到线性可分的线即可。