caffe 学习(2)——基本原理
参考 http://caffe.berkeleyvision.org/tutorial/
- 表达:models和optimizations使用纯文本文档形式定义,不是用代码定义;
- 速度:适用于工业和科研中的模型和大数据
- 模块性:新任务和设置可以灵活扩展
- 开源、社区
开始学习!
Blobs, Layers, and Nets: 一个Caffe模型的基本组成
Blobs: 标准数组和统一内存接口,用于存储、通信和操作信息(数据和偏导流)
Layers:模型和计算
Nets:连接层
Blobs:
blob实际上是caffe中处理和传输的数据的包装器,并同时兼具CPU和GPU之间的数据同步的能力。
数学上看,一个blob实际上是一个类似C中的N维数组。
caffe使用blob存储和通信数据。blob提供一个统一的内存接口保存数据。caffe中常用的数据有image batches, model parameters and derivatives for optimization。
由于我们通常对于blobs的数值和差分感兴趣,所以一个blob存储两块内存:data and diff。前者是我们传输的正常数据,后者是网络计算的梯度。
实际数据可以被存储在CPU或GPU上,我们有两种方式获得它们:const方式(不改变数值),mutable方式(改变数值)。两种方式如下定义:
const Dtype* cpu_data() const; Dtype* mutable_cpu_data();
在GPU上和对差分的操作是类似的。
这样设计的原因在于:blob使用SyncedMem类同步CPU和GPU的数据,为了隐藏同步的细节和最小化数据传输使用两种调用方式。
经验方法是如果不想改变数值就一直使用const方式调用,不在自己定义的object上存储指针。
Layers:
layer是模型的关键,计算的基础单元。layer的操作有卷积、pool、内积、应用非线性elementwise变换(ReLU,sigmoid等),normalize,加载数据,计算损失(softmax和hinge)等。
每个layer从底层连接获得输入,输出到顶层连接。
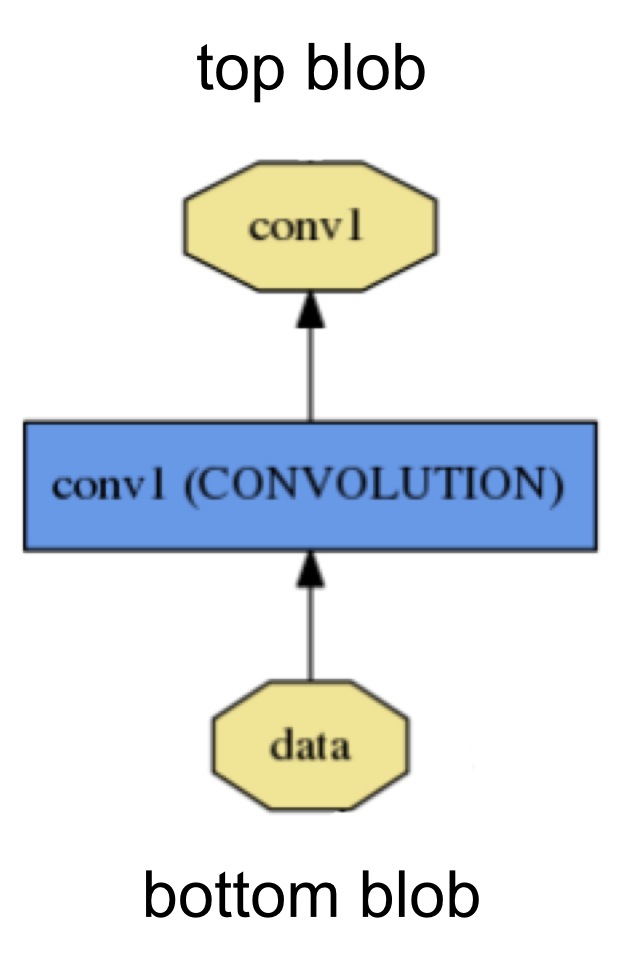
每个layer定义三种关键计算:setup,forward和backward。
setup:模型初始化时,初始化这个layer和它的连接;
forward:从底层取出输入,计算输出,传递到顶层;
backward:从顶层获得输入,计算梯度,发送到底层。有参数的层计算关于它的参数的梯度,并在内部存储。
特别地,每个layer有两种forward和backward实现,分别是基于CPU和GPU。如果没有实现GPU版本,layer默认使用CPU函数,这给快速实验带来了便利。
Nets:
net联合定义一个函数和它的梯度通过合成和自动差分。每个layer的输出的合成计算一个给定任务的函数,每个layer的backward的合成计算学习任务的loss的梯度。
caffe model是端到端的机器学习引擎。
net是layers的集合,layers之间使用有向无环图(Directed acyclic graph, DAG)连接。
net使用纯文本文档定义layers和他们指尖的连接。一个简单的logistic regression分类器如下定义:
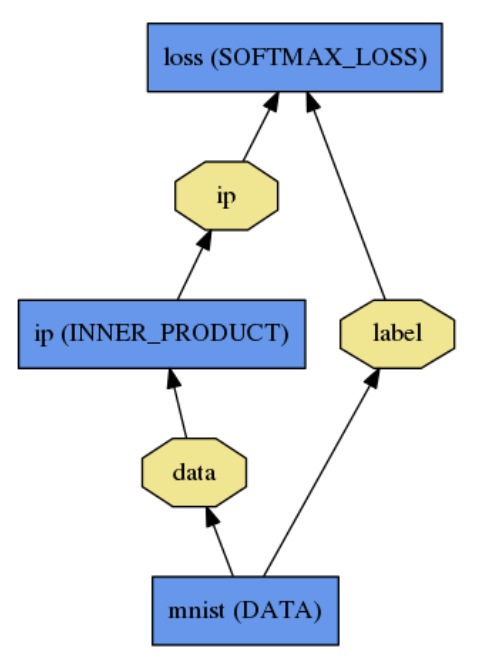
name: "LogReg"
layer {
name: "mnist"
type: "Data"
top: "data"
top: "label"
data_param {
source: "input_leveldb"
batch_size: 64
}
}
layer {
name: "ip"
type: "InnerProduct"
bottom: "data"
top: "ip"
inner_product_param {
num_output: 2
}
}
layer {
name: "loss"
type: "SoftmaxWithLoss"
bottom: "ip"
bottom: "label"
top: "loss"
}
模型初始化使用Net::Init().这个初始化主要做两件事:创建blobs和layers搭建整个有向无环图(DAG),调用layers的Setup()函数。它也做一些统计工作,例如校验整个网络架构的正确性。
注意:网络的构建是设备无关的。构建之后,网络是运行在CPU或GPU上是通过一个单独的定义实现的Caffe::mode(),设置Caffe::set_mode()。
模型是在纯文本protocol buffer模式.prototxt中定义的,学习好的模型被序列化为binary protocol buffer,存储在 .caffemodel文件中。
caffe使用Google Protocol Buffer出于以下几个优点:
序列化时最小化binary string的size,有效序列化,文本格式兼容binary version,在多种语言中都有接口实现,例如C++和Python。这些优点使得在caffe建模灵活可拓展。
Forward and Backward: 前线传播和后向传播
前向传播和后向传播是一个网络的关键计算。
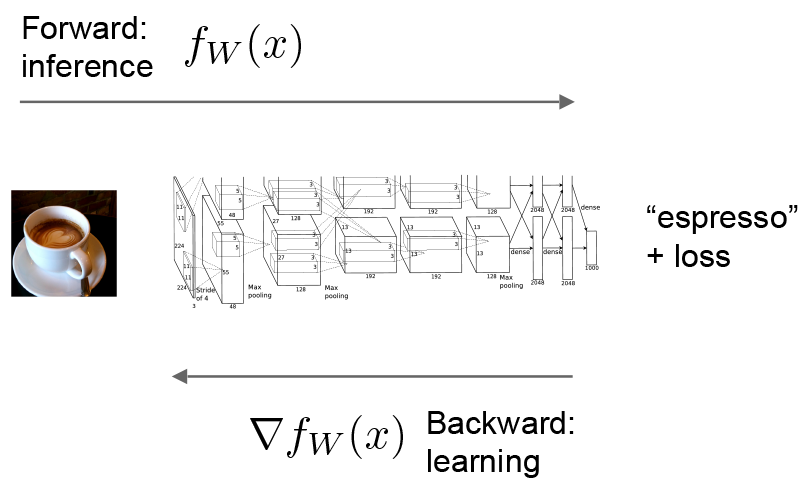
以简单的logistic regression为例:
前向传播计算给定输入的输出,caffe依次排列每个layer定义的计算操作,计算模型表达的函数。前向传播方向自底向上:
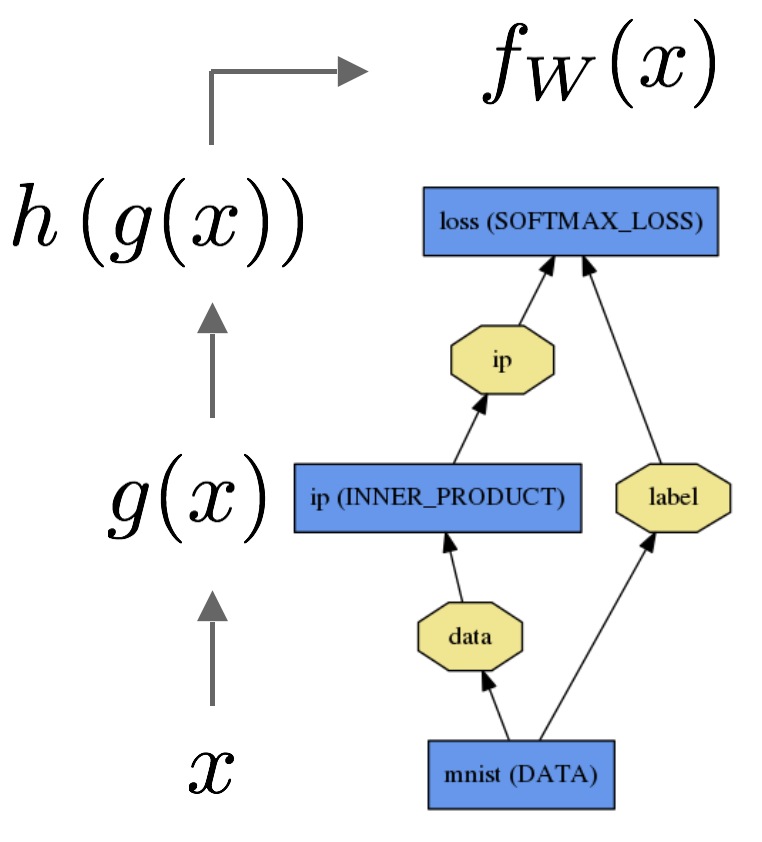
输入数据x通过一个内积层输出g(x),接着再通过一个softmax计算获得h(g(x)),得到输出softmax loss。
后向传播计算给定的loss的梯度。后向传播时,caffe逆向排列每层定义的梯度,通过自动差分计算整个模型的梯度。后向传播方向自顶向下:
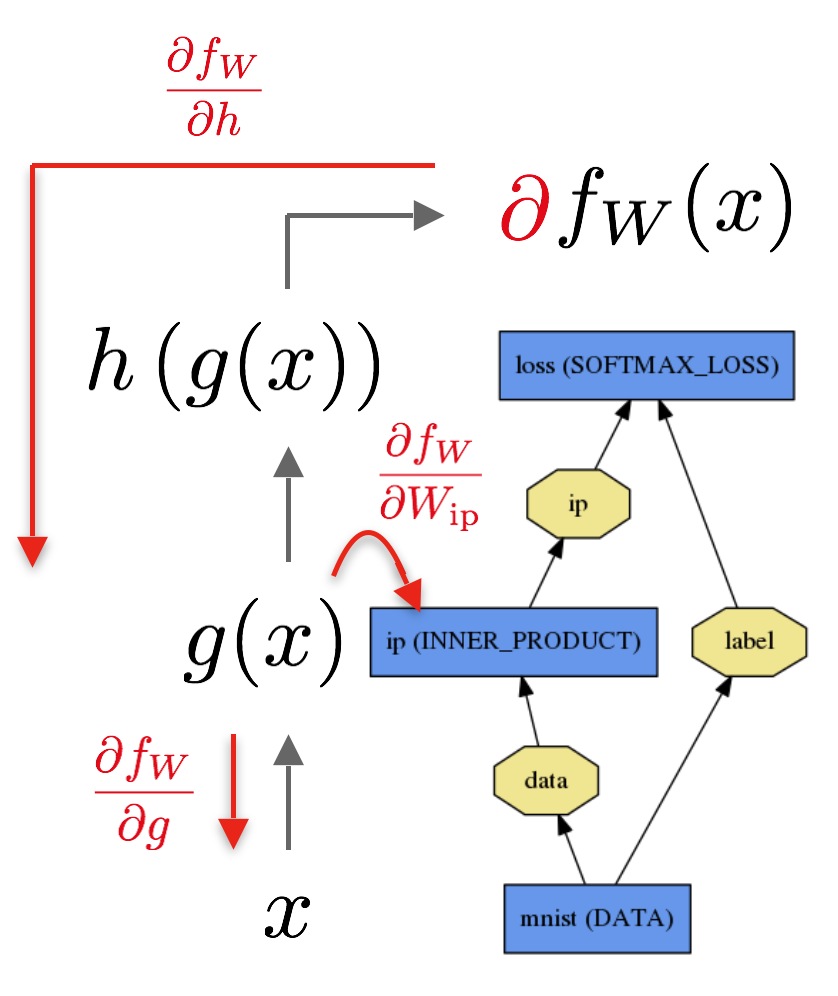
后向传播从loss开始,计算loss关于输出的梯度∂fw/∂h。关于模型剩余部分的梯度被一层层的根据链式法则求解。有参数的layer,像INNER_PRODUCT layer,计算关于layer参数的梯度∂fw/∂Wip,用于更新layer参数。
这些计算从定义model开始立即生效,caffe自动计划和执行前向和后向传播:
Net::Forward()和Net::Backward()方法执行相关的传播,而Layer::Forward()和Layer::Backward()在每个步骤中负责具体计算;
每个layer的计算类型有cpu和gpu两种(forward_{cpu, gpu}(), backward_{cpu, gpu}())。处于便利或限制因素考虑,一个layer允许只实现CPU或GPU版本。
Solver最优化一个model通过首先调用前向传播获得output和loss,然后调用后向传播生成model的梯度,更新weight和参数,以最小化loss。
Solver,Net,和Layer之间的分工使得caffe模块化,易于开发使用。
Loss:损失函数
caffe中,像众多机器学习技术一样,learning过程有loss function驱动。loss function也常被称为error,cost或objective function。损失函数指定了学习的目标,将参数设置(也就是当前网络的权重)映射为一个标量数值,来表达这些参数设置的“badness”程度。因此,学习的目标就是找出一组参数设置最小化损失函数。
caffe里的loss通过网络的前向传播计算。每个layer取一组输入(bottom)blobs,产生一组输出(top)blobs。这些layer的输出可能用于计算loss function。在one-verse-all分类任务中,loss function的一个典型选择是SoftmaxWithLoss函数,网络定义中如下定义:
layer {
name: "loss"
type: "SoftmaxWithLoss"
bottom: "pred"
bottom: "label"
top: "loss"
}
在一个SoftmaxWithLoss函数中,top blobs是一个标量,取整个mini-batch的loss的平均值(mini-batch中每个样本的预测label pred 与实际label label的误差的平均值)。
Loss Weights:
对于有多个layer的net来说,每个layer产生一个loss,loss weights用来指定这些loss的相对重要性。
按照约定,caffe中类型type中带有后缀Loss的layer对loss function有贡献,而其他的layers被默认为纯粹用于中间计算。然而,任何layer都可以被用作loss,通过在layer定义中添加一个field: loss_weight: <float>。每个带有后缀Loss的layer默认loss_weight:1对于第一个top blob,其他的top blob的loss_weight:0;其它layer默认对所有top blob的loss_weight:0。所以上面的SoftmaxWithLosslayer等价于如下定义
layer {
name: "loss"
type: "SoftmaxWithLoss"
bottom: "pred"
bottom: "label"
top: "loss"
loss_weight: 1
}
然而,任何能够后向传播的layer都可能被给一个非零的loss_weight,例如允许正则化网络中间层的激励。对于非单个输出的layer,如果被赋予一个非零loss_weight,loss通过对blob的所有元素求和简单计算。
caffe中最终loss通过网络的总体加权loss的求和被计算,如下伪码所示:
loss := 0
for layer in layers:
for top, loss_weight in layer.tops, layer.loss_weights:
loss += loss_weight * sum(top)
Solver:
solver精心排列网络的前向推断和后向梯度构成参数更新过程,以保证loss最小化。学习过程被分为Solver监督管理最优化和生成参数更新过程,Net计算loss和梯度。
caffe的solver包括:
- Stochastic Gradient Descent (
type: "SGD"), - AdaDelta (
type: "AdaDelta"), - Adaptive Gradient (
type: "AdaGrad"), - Adam (
type: "Adam"), - Nesterov’s Accelerated Gradient (
type: "Nesterov") and - RMSprop (
type: "RMSProp")
Solver构建最优化过程,创建学习的训练网络和评估的测试网络;迭代地调用forward/backward函数和更新参数;周期性地评估测试网络;在最优化过程中给model和solver状态拍快照(缓存?)
在每个迭代步骤中,调用网络前向传播计算输出和loss;调用网络后向传播计算梯度;根据solver方法,将所得梯度用于参数更新;根据学习率,history,和方法更新solver状态。
像caffe的model一样,caffe solver有CPU和GPU两种模式。
solver方法针对于解决loss最小化的一般最优化问题。对数据集D,最优化目标是所有数据的平均loss,如下式所示:
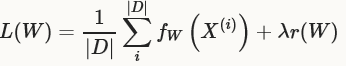
其中fW(X(i))是数据项X(i)的loss,r(W)是正则化项。|D|在实际中可能非常大,所以在每个solver迭代过程中,我们使用目标的stochastic近似,使用一个mini-batch的数据N<<|D|,loss如下所示:
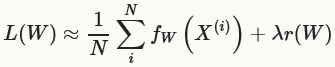
model计算前向传播时计算fW,后向传播时计算梯度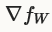 。
。
参数更新 被solver构建,来源于error梯度
被solver构建,来源于error梯度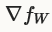 ,正则化梯度和其他特定项。
,正则化梯度和其他特定项。
SGD:Stochastic gradient descent (type: "SGD")
更新权重W通过一个线性联合负梯度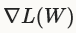 和先前的权重更新
和先前的权重更新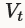 。学习率α是负梯度的加权系数,momentum μ是前面权重更新的加权系数。
。学习率α是负梯度的加权系数,momentum μ是前面权重更新的加权系数。
一般情况下,我们使用下面公式根据以前权重更新Vt和当前权重Wt,计算迭代次数为t+1时的更新值Vt+1和更新权重Wt+1:

学习过程的超参数("hyperparameters" α和μ)可能需要一些调整以获得最后的结果。如果不确定从哪里开始调整,参考下面的经验法则("Rules of thumb"),更多的信息可以参见Leon Bottou's Stochastic Gradient Descent Tricks(L. Bottou. Stochastic Gradient Descent Tricks. Neural Networks: Tricks of the Trade: Springer, 2012.)。
设置学习率α和momentum μ的经验法则:
使用SGD方法的deep learning,初始化学习率的一个好的策略是设置一个值约 ,然后在训练过程中,每当loss达到一个明显的谷点时,使它降低一个常数因子(例如10),这个过程重复几次。通常情况下momentum μ = 0.9或相似的值。通过在迭代中平滑权重更新,momentum使得基于SGD的deep learning过程更平稳更快。
,然后在训练过程中,每当loss达到一个明显的谷点时,使它降低一个常数因子(例如10),这个过程重复几次。通常情况下momentum μ = 0.9或相似的值。通过在迭代中平滑权重更新,momentum使得基于SGD的deep learning过程更平稳更快。
这是Krizhevsky et al.[1]中使用的策略。caffe使得这个策略在SolverParameter中很容易实现,见./example/imagenet/alexnet_solver.prototxt。
如要使用这样的超参数调整策略,你可以将下面几行放入你的solver的prototxt中的某位置:
base_lr: 0.01 # begin training at a learning rate of 0.01 = 1e-2
lr_policy: "step" # learning rate policy: drop the learning rate in "steps"
# by a factor of gamma every stepsize iterations
gamma: 0.1 # drop the learning rate by a factor of 10
# (i.e., multiply it by a factor of gamma = 0.1)
stepsize: 100000 # drop the learning rate every 100K iterations
max_iter: 350000 # train for 350K iterations total
momentum: 0.9
上面的设置中,momentum μ始终等于0.9。训练开始时的前100,000次迭代,学习率base_lr  ,然后乘以gamma,以学习率
,然后乘以gamma,以学习率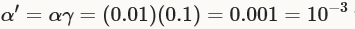 训练第100K-200K次迭代,然后第200K至300K迭代使用学习率
训练第100K-200K次迭代,然后第200K至300K迭代使用学习率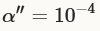 ,最后直到350K次迭代,学习率为
,最后直到350K次迭代,学习率为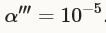 。
。
注意到在很多次迭代后,momentum μ有效地使用一个因子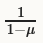 乘以更新的size,所以如果增加μ,也应该相应地降低学习率α。反之亦然。
乘以更新的size,所以如果增加μ,也应该相应地降低学习率α。反之亦然。
例如μ = 0.9时,我们有一个有效地更新size乘子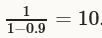 ;如果我们增加momentum到μ = 0.99时,我们已经增加更新size乘子到100,所以应该降低学习率以一个因子10(乘以0.1)。
;如果我们增加momentum到μ = 0.99时,我们已经增加更新size乘子到100,所以应该降低学习率以一个因子10(乘以0.1)。
注意上面的设置仅仅是指导作用,并不保证在每种情况下最优,甚至某些情况下根本就无效。如果学习过程中,例如初夏非常大的或者NaN或者inf的loss值或输出,尝试降低初始学习率base_lr,重新训练,直到你发现base_lr值有效。
[1] A. Krizhevsky, I. Sutskever, and G. Hinton. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems, 2012.
AdaDelta: (type: "AdaDelta")
这个方法是一个"稳定学习率的方法“,它像SGD一样基于梯度进行最优化,更新形式如下:

[1] M. Zeiler ADADELTA: AN ADAPTIVE LEARNING RATE METHOD. arXiv preprint, 2012.
RMS:均方根值,Root-Mean-Square
AdaGrad: adaptive gradient (type: "AdaGrad")
是一个类似于SGD的基于梯度的优化算法,企图以非常的predictive但几乎看不见的特征的形式进行大海捞针("find needles in haystacks in the form of very predictive but rarely seen features", in Duchi et al.'s words)。给定所有前面迭代时的更新信息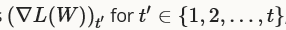 ,更新公式如下所示:
,更新公式如下所示:
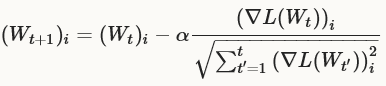
实际上,对于权重W 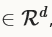 ,AdaGrad实现使用仅仅O(d)的额外存储空间为历史gradient信息。
,AdaGrad实现使用仅仅O(d)的额外存储空间为历史gradient信息。
[1] J. Duchi, E. Hazan, and Y. Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. The Journal of Machine Learning Research, 2011.
Adam:(type: "Adam")
也是基于梯度的最优化方法,包含一个自适应矩估计(mt,vt),能够被视为AdaGrad的推广,更新形式如下:
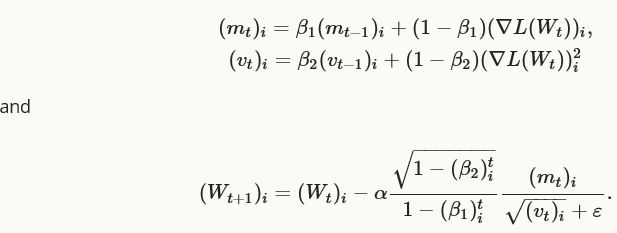
Kingma等人提出使用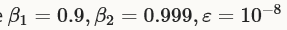 作为默认值,caffe使用momentum, momentum2, delta分别表示
作为默认值,caffe使用momentum, momentum2, delta分别表示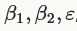 。
。
[1] D. Kingma, J. Ba. Adam: A Method for Stochastic Optimization. International Conference for Learning Representations, 2015.
NAG: Nesterov's accelerated gradient (type: "Nesterov")
是一种最优的凸优化方法,实现了收敛率 ,而不是
,而不是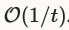 。尽管实现
。尽管实现 收敛率所要求的假设典型地不支持使用caffe训练的神经网络,由于非平滑性和非凸性。实际中NAG是一种非常有效的方法,去最优化特定形式的deep learning架构,例如Sutskever等人生命的deep MNIST autoencoders。
收敛率所要求的假设典型地不支持使用caffe训练的神经网络,由于非平滑性和非凸性。实际中NAG是一种非常有效的方法,去最优化特定形式的deep learning架构,例如Sutskever等人生命的deep MNIST autoencoders。
权重更新看起来与SGD非常相似:
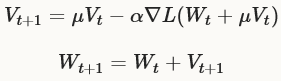
与SGD的区别在于SGD中使用梯度中的W不同,SGD中权重设置W基于误差梯度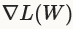 ,NAG中我们采用权重加上momentum
,NAG中我们采用权重加上momentum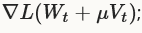 。
。
[1] Y. Nesterov. A Method of Solving a Convex Programming Problem with Convergence Rate O(1/k)
. Soviet Mathematics Doklady, 1983.
[2] I. Sutskever, J. Martens, G. Dahl, and G. Hinton. On the Importance of Initialization and Momentum in Deep Learning. Proceedings of the 30th International Conference on Machine Learning, 2013
RMSprop: (type: "RMSprop")
是一个基于梯度的最优化方法,更新形式如下:
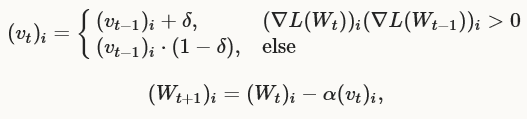
如果梯度更新导致震荡,梯度降低为(1 - δ)倍,否则增加δ。默认的δ值(rms_decay)为0.02。
[1] T. Tieleman, and G. Hinton. RMSProp: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning.Technical report, 2012.
Scaffolding:拍快照
solver的scanffolding准备最优化方法和崔思华模型在Solver::Presolve()方法中。
> caffe train -solver examples/mnist/lenet_solver.prototxt
I0902 13:35:56.474978 16020 caffe.cpp:90] Starting Optimization
I0902 13:35:56.475190 16020 solver.cpp:32] Initializing solver from parameters:
test_iter: 100
test_interval: 500
base_lr: 0.01
display: 100
max_iter: 10000
lr_policy: "inv"
gamma: 0.0001
power: 0.75
momentum: 0.9
weight_decay: 0.0005
snapshot: 5000
snapshot_prefix: "examples/mnist/lenet"
solver_mode: GPU
net: "examples/mnist/lenet_train_test.prototxt"
Net initialization
I0902 13:35:56.655681 16020 solver.cpp:72] Creating training net from net file: examples/mnist/lenet_train_test.prototxt
[...]
I0902 13:35:56.656740 16020 net.cpp:56] Memory required for data: 0
I0902 13:35:56.656791 16020 net.cpp:67] Creating Layer mnist
I0902 13:35:56.656811 16020 net.cpp:356] mnist -> data
I0902 13:35:56.656846 16020 net.cpp:356] mnist -> label
I0902 13:35:56.656874 16020 net.cpp:96] Setting up mnist
I0902 13:35:56.694052 16020 data_layer.cpp:135] Opening lmdb examples/mnist/mnist_train_lmdb
I0902 13:35:56.701062 16020 data_layer.cpp:195] output data size: 64,1,28,28
I0902 13:35:56.701146 16020 data_layer.cpp:236] Initializing prefetch
I0902 13:35:56.701196 16020 data_layer.cpp:238] Prefetch initialized.
I0902 13:35:56.701212 16020 net.cpp:103] Top shape: 64 1 28 28 (50176)
I0902 13:35:56.701230 16020 net.cpp:103] Top shape: 64 1 1 1 (64)
[...]
I0902 13:35:56.703737 16020 net.cpp:67] Creating Layer ip1
I0902 13:35:56.703753 16020 net.cpp:394] ip1 <- pool2
I0902 13:35:56.703778 16020 net.cpp:356] ip1 -> ip1
I0902 13:35:56.703797 16020 net.cpp:96] Setting up ip1
I0902 13:35:56.728127 16020 net.cpp:103] Top shape: 64 500 1 1 (32000)
I0902 13:35:56.728142 16020 net.cpp:113] Memory required for data: 5039360
I0902 13:35:56.728175 16020 net.cpp:67] Creating Layer relu1
I0902 13:35:56.728194 16020 net.cpp:394] relu1 <- ip1
I0902 13:35:56.728219 16020 net.cpp:345] relu1 -> ip1 (in-place)
I0902 13:35:56.728240 16020 net.cpp:96] Setting up relu1
I0902 13:35:56.728256 16020 net.cpp:103] Top shape: 64 500 1 1 (32000)
I0902 13:35:56.728270 16020 net.cpp:113] Memory required for data: 5167360
I0902 13:35:56.728287 16020 net.cpp:67] Creating Layer ip2
I0902 13:35:56.728304 16020 net.cpp:394] ip2 <- ip1
I0902 13:35:56.728333 16020 net.cpp:356] ip2 -> ip2
I0902 13:35:56.728356 16020 net.cpp:96] Setting up ip2
I0902 13:35:56.728690 16020 net.cpp:103] Top shape: 64 10 1 1 (640)
I0902 13:35:56.728705 16020 net.cpp:113] Memory required for data: 5169920
I0902 13:35:56.728734 16020 net.cpp:67] Creating Layer loss
I0902 13:35:56.728747 16020 net.cpp:394] loss <- ip2
I0902 13:35:56.728767 16020 net.cpp:394] loss <- label
I0902 13:35:56.728786 16020 net.cpp:356] loss -> loss
I0902 13:35:56.728811 16020 net.cpp:96] Setting up loss
I0902 13:35:56.728837 16020 net.cpp:103] Top shape: 1 1 1 1 (1)
I0902 13:35:56.728849 16020 net.cpp:109] with loss weight 1
I0902 13:35:56.728878 16020 net.cpp:113] Memory required for data: 5169924
Loss
I0902 13:35:56.728893 16020 net.cpp:170] loss needs backward computation.
I0902 13:35:56.728909 16020 net.cpp:170] ip2 needs backward computation.
I0902 13:35:56.728924 16020 net.cpp:170] relu1 needs backward computation.
I0902 13:35:56.728938 16020 net.cpp:170] ip1 needs backward computation.
I0902 13:35:56.728953 16020 net.cpp:170] pool2 needs backward computation.
I0902 13:35:56.728970 16020 net.cpp:170] conv2 needs backward computation.
I0902 13:35:56.728984 16020 net.cpp:170] pool1 needs backward computation.
I0902 13:35:56.728998 16020 net.cpp:170] conv1 needs backward computation.
I0902 13:35:56.729014 16020 net.cpp:172] mnist does not need backward computation.
I0902 13:35:56.729027 16020 net.cpp:208] This network produces output loss
I0902 13:35:56.729053 16020 net.cpp:467] Collecting Learning Rate and Weight Decay.
I0902 13:35:56.729071 16020 net.cpp:219] Network initialization done.
I0902 13:35:56.729085 16020 net.cpp:220] Memory required for data: 5169924
I0902 13:35:56.729277 16020 solver.cpp:156] Creating test net (#0) specified by net file: examples/mnist/lenet_train_test.prototxt
Completion
I0902 13:35:56.806970 16020 solver.cpp:46] Solver scaffolding done.
I0902 13:35:56.806984 16020 solver.cpp:165] Solving LeNet# The snapshot interval in iterations.
snapshot: 5000
# File path prefix for snapshotting model weights and solver state.
# Note: this is relative to the invocation of the `caffe` utility, not the
# solver definition file.
snapshot_prefix: "/path/to/model"
# Snapshot the diff along with the weights. This can help debugging training
# but takes more storage.
snapshot_diff: false
# A final snapshot is saved at the end of training unless
# this flag is set to false. The default is true.
snapshot_after_train: true∇




