[转]C++11 随机数学习
相对于C++ 11之前的随机数生成器来说,C++11的随机数生成器是复杂了很多。这是因为相对于之前的只需srand、rand这两函数即可获取随机数来说,C++11提供了太多的选择和东西。
随机数生成算法:
随机数生成算法有很多,C++11之前的C/C++只用了一种。C++11则提供下面三种可供选择:
linear_congruential_engine线性同余法
mersenne_twister_engine梅森旋转法
substract_with_carry_engine滞后Fibonacci
这三种算法,在C++11里面都是用模板的方式实现的。如果我们要使用这三个模板类的话,就必须自己实例化之。但这些实例化参数都是这些算法里面使用到的参数,如果不懂算法的原理的话,真的不知道需要用什么参数才能得到比较好的随机序列。所以我们这些卑微的码农是用不了这些模板类的。C++11标准也想到了这点,所以就帮我们预定义了一些随机数类,这些随机数类都是用比较好的参数实例化上面那三个模板类。注意:在C++11里面,把这些随机数生成器叫做引擎(engines)。
下图列出了一些实例化的随机数类: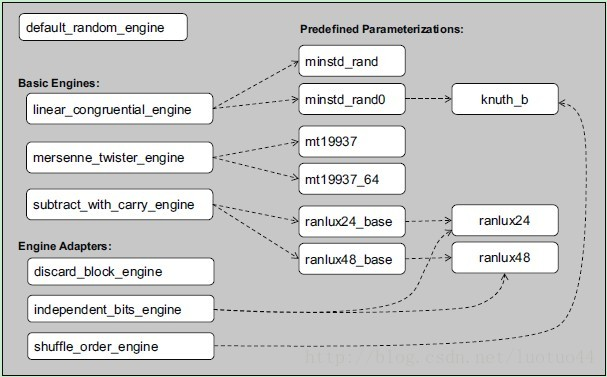
当然具体用了哪些参数,我们是不用管的,直接用就行了。
在上图的左上角,还可以看到一个default_random_engine的类。它也是一个实例化的类。之所以不归入那三种算法,是因为它的实现是由编译器厂家决定的,有的可能用linear_congruential_engine实现,有的可能用mersenne_twister_engine实现。这种现象在C/C++中见多了。不过,对于其他的类,C++11是有明确规定用哪种算法和参数实现的。
好了,说了这么多还是上一个例子吧。
#include<iostream>
#include<random>
usingstd::cout;
usingstd::endl;
usingstd::cin;
intmain()
{
std::default_random_engine random;
for(int i = 0; i < 20; ++i)
cout<<random()<<' ';
cout<<endl;
return 0;
}
//gcc编译器需要加上 –std=c++11 选项。
C++11中,随机数都是定义在random头文件中的。除了default_random_engine,其他的那些实例化随机数类的名字都是怪怪的,所以还是这个好用。从例子中可以看到,是通过operator ()函数来获取下一个随机数。
对srand熟悉的码农们肯定发现,这里没有使用到随机数种子。其实这里使用了默认种子,默认种子的值可以通过这类的公共静态常量default_seed来获取。如果想为这个类设置自己的种子的话,那么可以通过在构造函数中传入一个参数。也可以在构造之后调用seed()成员函数设置种子。
产生均匀分布的随机数:
上面例子产生的随机数会比较大,如果我们只想产生0到100的随机数。按照我们之前的做法是直接random()%100。这种做法是不好的。原因可以参见《Accelerated C++》的7.4.4节。
C++11也知道这一点,这就使得C++11的随机数更加复杂了。
我们平常说产生随机数,隐含是意思是产生均匀分布的随机数。学过概率论的同学都知道,除了均匀分布还有很多分布,比如正态分布、泊松分布等等。之前在网上看过网友怎么用rand()函数产生的随机数制作这些分布。现在这工作不用码农做了,C++11标准都提供了这些分布。
C++11提供的均匀分布模板类为:uniform_int_distribution和uniform_real_distribution。前一个模板类名字中的int不是代表整型,而是表示整数。因为它是一个模板类,可以用int、long、short等整数类型来实例化。后一个表示浮点数模板类,可以用float和double来实例化。使用例子如下:
#include<iostream>
#include<random>
#include<time.h>
using std::cout;
using std::endl;
using std::cin;
int main()
{
std::default_random_engine random(time(NULL));
std::uniform_int_distribution<int> dis1(0, 100);
std::uniform_real_distribution<double> dis2(0.0, 1.0);
for(int i = 0; i < 10; ++i)
cout<<dis1(random)<<' ';
cout<<endl;
for(int i = 0; i < 10; ++i)
cout<<dis2(random)<<' ';
cout<<endl;
return 0;
}
可以看到,在uniform_int_distribution的构造函数中,参数说明了随机数的范围。uniform_int_distribution的随机数的范围不是半开范围[ ),而是[ ],对于uniform_real_distribution却是半开范围[ )。也是就是说上面的例子中,能产生100,但不会产生1.0。不得不说,这颠覆了之前的认识。对于default_random_engine来说,其产生的随机数范围是在[min(), max()]之间,其中min()和max()为它的两个成员函数。同样,也是非半开范围。对于浮点数,如果真的是想产生[0.0, 1.0]范围的数,可以使用
#include<cmath> #include<cfloat> std::uniform_real_distribution<double> dis2(0, std::nextafter(1,DBL_MAX));
如果uniform_int_distribution使用了无参构造函数,那么其随机数的范围是[0,numberic_limits<type>::max()],也就是0到对应实例化类型能表示的最大值。对于uniform_real_distribution的无参构造函数,则是[0, 1)。
mt19937
当你第一眼看到这玩意儿的时候
肯定禁不住吐槽:纳尼?这是什么鬼?
确实,这个东西鲜为人知,但是它却有着卓越的性能
简介
mt19937是c++11中加入的新特性
它是一种随机数算法,用法与rand()函数类似
但是具有速度快,周期长的特点(它的名字便来自周期长度:2^19937-1)
说的直白一点,我们都知道rand()在windows下生成的数据范围为0-32767
但是这个函数的随机范围大概在(−maxint,+maxint)(−maxint,+maxint)(maxint为int类型最大值)
实例
这个东西用法非常简单
#include<random>
#include<ctime>
std::mt19937 rnd(time(0));
int main()
{
printf("%lld\n",rnd());
return 0;
}
概率分布类型:
C++11提供的概率分布类型有下面这些:
均匀分布:
uniform_int_distribution 整数均匀分布
uniform_real_distribution 浮点数均匀分布
伯努利类型分布:(仅有yes/no两种结果,概率一个p,一个1-p)
bernoulli_distribution 伯努利分布
binomial_distribution 二项分布
geometry_distribution 几何分布
negative_biomial_distribution 负二项分布
Rate-based distributions:
poisson_distribution 泊松分布
exponential_distribution指数分布
gamma_distribution 伽马分布
weibull_distribution 威布尔分布
extreme_value_distribution 极值分布
正态分布相关:
normal_distribution 正态分布
chi_squared_distribution卡方分布
cauchy_distribution 柯西分布
fisher_f_distribution 费歇尔F分布
student_t_distribution t分布
分段分布相关:
discrete_distribution离散分布
piecewise_constant_distribution分段常数分布
piecewise_linear_distribution分段线性分布
这些概率分布函数都是有参数的,在类的构造函数中把参数传进去即可。
下面是一个泊松分布的例子
#include<iostream>
#include<random>
#include<time.h>
#include<iomanip>
intmain()
{
const int nrolls = 10000; // number ofexperiments
const int nstars = 100; // maximum number of stars to distribute
int parameter = 4;
std::minstd_rand engine(time(NULL));
std::poisson_distribution<int>distribution(parameter);
int p[20]={};
for (int i=0; i<nrolls; ++i)
{
int number = distribution(engine);
if (number < 20)
++p[number];
}
std::cout << "poisson_distribution"<<parameter<< std::endl;
for (int i=0; i < 20; ++i)
std::cout<<std::setw(2)<< i<< ": " << std::string(p[i]*nstars/nrolls, '*') <<std::endl;
return 0;
}
某一个输出结果为:

可能大家都忘了泊松分布了,看一下下面的图吧

真正的随机数:
C++11还提供了一个random_device随机数类。它并不是由某一个数学算法得到的随机序列,而是通过读取文件,读什么文件看具体的实现(Linux可以通过读取/dev/random文件来获取)。文件的内容是随机的,因为文件内容是计算机系统的熵(熵指的是一个系统的混乱程度)。也是当前系统的环境噪声,系统噪音可以通过很多参数来评估,如内存的使用,文件的使用量,不同类型的进程数量等等。Linux的熵来自键盘计时、鼠标移动等。
不过gcc好像并没有很好地实现这个类,我手里的Mingw4.9.0就不随机,每次运行都得到同样的序列。
对于C++11的随机类的更多用法可以参考这里。
参考:《C++标准库 ——自学教程与参考手册》(第2版)
《C++ Primer》(第5版)
http://blog.csdn.net/akonlookie/article/details/8223525
http://stackoverflow.com/questions/19665818/best-way-to-generate-random-numbers-using-c11-random-library?rq=1
http://hipercomer.blog.51cto.com/4415661/857870



 浙公网安备 33010602011771号
浙公网安备 33010602011771号