简单数论(三)-----欧拉定理
欧拉定理总结
Part I 欧拉函数
ø(n)是欧拉函数,表示小于正整数n的数中与n互质的数的个数
Part II 欧拉函数的性质
1. 若p为某一素数,则ø(p)=p-1
2. 若p为某一素数,
则ø(pa)=(p-1)*pa-1
证明:比pa小的数有pa-1个,其中,所有能被p整除的数可以表示成p*k(k = 1,2,3...,pa-1-1),
这些数肯定不与pa互质,其余的数都与pa互质 ∴ø(pa)=pa-1-(pa-1-1)=(p-1)*pa-1
3. 若a、b互质,则ø(a*b)=ø(a)*ø(b)
4.任意正整数n=p1a1*p2a2*...*pkak,p1~pk为素数,则
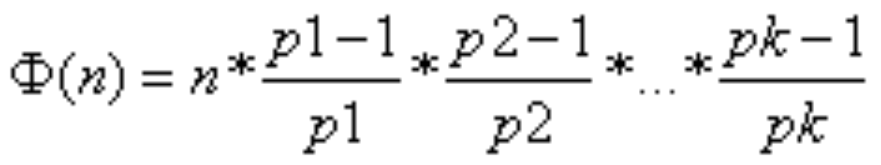
4.求单个欧拉函数的代码

5.欧拉函数的线性筛法
求一个正整数n的欧拉函数值为O(n)
如何在线性时间内求出所有数的欧拉函数值?
需要先了解如下两个性质
若i mod p = 0,那么ø(i*p)=p*ø(i)
若i mod p ≠ 0,那么ø(i*p)=(p-1)*ø(i)
6.欧拉筛参考代码
inline void get_phi() { phi[1]=1; for(int i=2;i<=MAXN;i++) { if(mark[i]==0){ ++tot; prime[tot] = i; phi[i] = i-1; } for(int j=1;j<=tot;j++) { if(i*prime[j]>MAXN) { break; } mark[i*prime[j]] = 1; if(i%prime[j]==0) { phi[i*prime[j]] = phi[i] * prime[j]; break; } else { phi[i*prime[j]] = phi[i] * (prime[j]-1); } } } }
Part III 欧拉定理及扩展欧拉定理
1.欧拉定理
若a与m互质,则aø(m)≡1(mod m)
2.扩展欧拉定理
其中
。



