「论文研究」三角梯结构——从一道 CTSC 的题的加强版谈起
先放一道加强题，以引出这篇论文。
这是一道交互题。
有一个小球集合，初始为空。每个小球有颜色，定义主要颜色为在当前小球集合中严格超过一半的颜色。你需要实现如下两个操作：
push：加入一个小球，编号为上一个小球的编号 \(+1\)，注意你不知道它的颜色；pop x：删除编号为 \(x\) 的小球；
在每次操作后，你都要输出 answer *：若存在主要颜色，返回任意一个在当前集合中的该颜色小球的编号；否则返回 -1。你不必实时输出答案，只要最后能依次输出这 \(q\) 个值即可。
你可以通过 test x y 询问交互库编号为 \(x\) 和 \(y\) 的小球颜色是否相等。
评分方式
我们记第 \(i\) 次 push 操作后询问次数为 \(C1_i\)，第 \(i\) 次 pop x 操作后询问次数为 \(C2_i\)，以及 \(f\) 表示是否实时输出答案（\(=1\) 为是，\(=0\) 为否）。
| # | \(q\) | \(C1_i\) | \(C2_i\) | \(\sum C1_i\) | \(\sum C2_i\) | \(f\) | 特殊性质 | 分值 |
|---|---|---|---|---|---|---|---|---|
| subtask 1 | \(\le 1000\) | \(\le q\) | \(\le q\) | / | / | / | / | 5 |
| subtask 2 | \(\le 10^5\) | \(\le 20\) | \(\le 20\) | / | / | \(=1\) | 数据随机 | 5 |
| subtask 3 | \(\le 10^5\) | / | / | \(\le 4\times 10^6\) | \(\le 4\times 10^6\) | / | / | 10 |
| subtask 4 | \(\le 5\times 10^4\) | \(\le 300\) | \(\le 300\) | / | / | \(=1\) | / | 10 |
| subtask 5 | \(\le 10^5\) | \(\le 10\) | \(\le 10\) | / | / | \(=1\) | / | 20 |
| subtask 6 | \(\le 10^5\) | \(\le 3\) | \(\le 4\) | / | / | \(=1\) | / | 20 |
| subtask 7 | \(\le 10^5\) | \(\le 2\) | \(\le 2\) | / | / | \(=1\) | / | 30 |
出题契机
本题灵感来源于「CTSC 2004」Stone Age，我在论文文献中翻阅到了此篇论文，并据此出了这样一道题。
题解
subtask 1
每次暴力问出加入的球的颜色即可。
操作次数 \(C1_i\le q\)，\(C2_i=0\)。
subtask 2
数据随机的情况下，若小球集合 \(> C\)（\(C\) 为一个常数），则基本不存在主要颜色。在 \(\le C\) 时可以通过扫一遍问出主要颜色。
操作次数 \(C1_i=C-1\)，\(C2_i=C-1\)。
subtask 3
可以离线，求出每个小球所在的时间区间，下放至线段树的 \(2\times \log q\) 个区间中。
考虑线段树分治，在每根线段时以「打擂台」的形式计算主要颜色即可。
操作次数 \(\sum C1_i=2q\log q\)。
subtask 4
留给奇怪的根号分治做法以及一些写萎了的做法。
subtask 5, 6, 7
我们设计一种数据结构，称之为“三角梯”。
三角梯，顾名思义，将点排成两排，以三角形的形状阶梯分布。
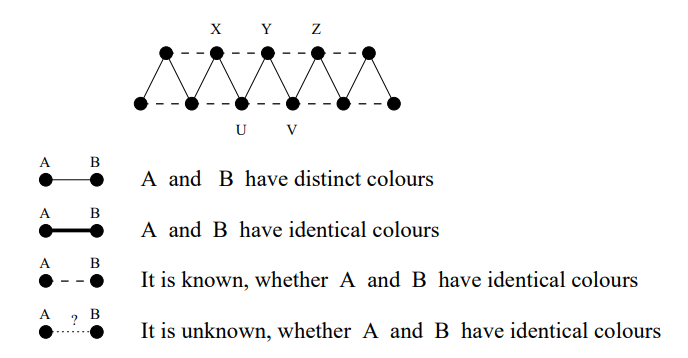
在这个三角梯中，相邻两点间的颜色关系是需要通过询问得到的。用细线表示不同色；用粗线表示同色；用虚线表示已经知道关系，但是为了之后方便描述插入、删除操作，我们暂时不关心它们具体啥关系；用虚线带“？”表示需要立刻询问它们的关系。
在操作的过程中，我们维护的“三角梯”始终会满足如下性质：
- 不在同一排的相邻点，必须不同色（细线）；
- 两排最左边的两个点相邻，不妨假设第二排最左边的点在第一行最左边的点的左下方；
- 第二排的点个数不少于第一排的点个数；
- 当没有主要颜色时，两排的点数差 \(\le 1\)；当有主要颜色时，两排的点数允许 \(>1\)，并且第二排的所有点均为该主要颜色。
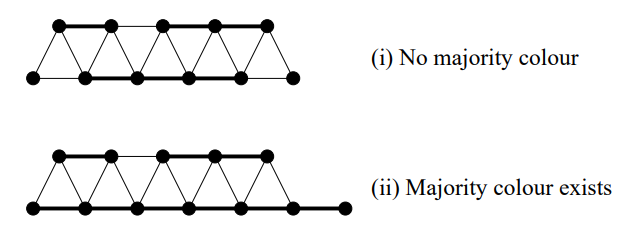
我们称同一排内极长同色段为一块（block）。由此可见，对于计算答案而言，我们只需判断第二排是否点数大于第一排，且仅有一块即可，时间复杂度 \(\mathcal O(1)\)。
插入
假设要插入的点为 \(Z\)。
- 若当前有主要颜色
记 \(A\) 为主要颜色块的最后一个点，我们根据 \(A\) 与 \(Z\) 的颜色关系分类即可。
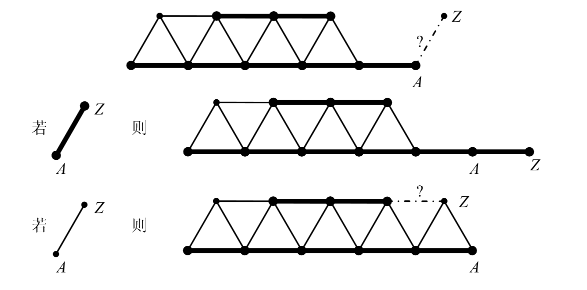
- 若当前没有主要颜色
我们同样可以分类讨论。注意 \(A\) 和 \(Z\) 同色时，要根据 \(U\) 和 \(V\) 是否同色分类的原因是论文用了链表去维护块，如果从中间某个位置把一个块断开，链表无法快速维护每个点所在块的信息（每个点需要记录块首和块尾是谁）。
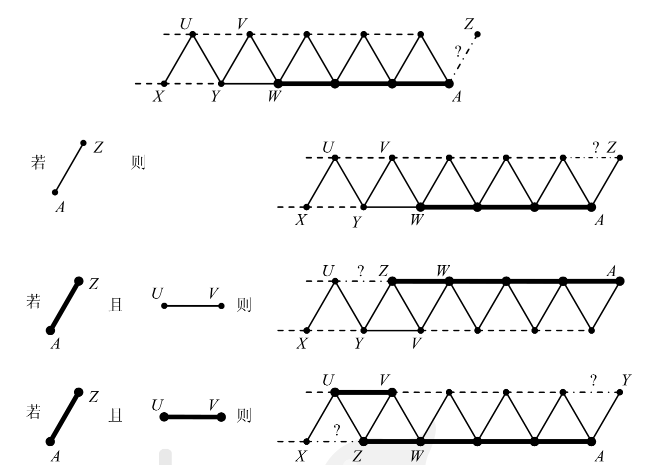
容易发现一次插入，最多导致 \(3\) 次询问花销。
如果我们采用平衡树去维护块（每个块本质上可以看成一个序列），那么只需要 \(2\) 次询问。
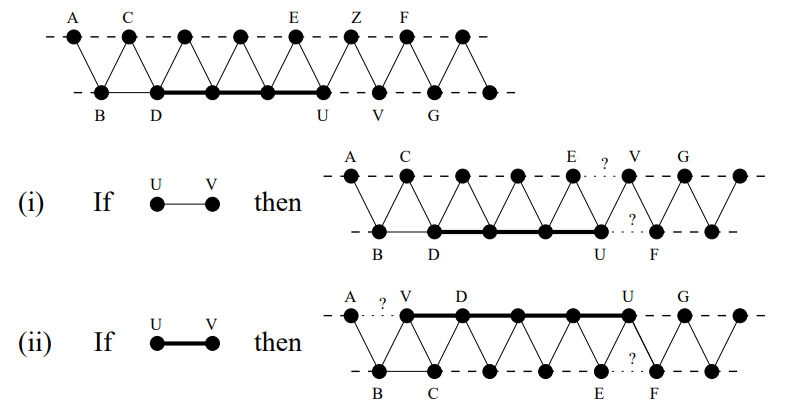
删除
删除基于插入。我们同样进行分类讨论。最多导致 \(4\) 次询问花销（\(1+3\)）。
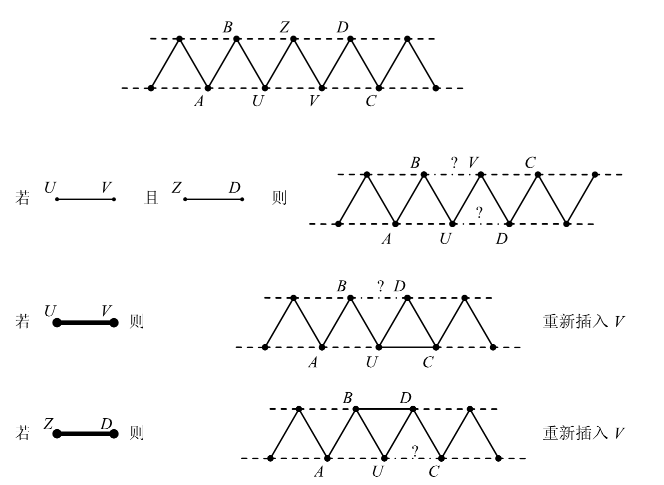
如果采用平衡树去维护，容易优化到 \(2\) 次询问。
整合
如果采用链表去维护，可以做到 \(C1_i\le 3\)，\(C2_i\le 4\)，时间复杂度 \(\mathcal O(q)\)；
如果采用平衡树去维护，可以做到 \(C1_i\le 2\)，\(C2_i\le 2\)，时间复杂度 \(\mathcal O(q\log q)\)；
可以获得满分。
