CF1588F Jumping Through the Array
在讲正解之前,先播一个小故事:
xay 复杂度错误过题。将操作按照时间分块,块内他令所有置换环都必须有至少一个“黑点”。
可以通过没有修改 \(p\) 操作,同时 \(p_i=i\),把黑点的个数卡到 \(O(n)\)。这样复杂度就是 \(O(nq\log n)\) 了。
CF1588F Jumping Through the Array
给定一个长为 \(n\) 的序列 \(a\) 以及排列 \(p\),实现以下操作:
- 给定 \(l,r\)。求 \(\sum\limits_{i=l}^{r} a_i\);
- 给定 \(x,y\)。我们将 \(i\to p_i\) 连成一个个置换环,将 \(x\) 所在环上的每个点点权加 \(y\);
- 给定 \(x,y\)。交换 \(p_x,p_y\)。
\(1\le n\le 2\cdot 10^5,-10^8\le a_i\le 10^8,1\le p_i\le n,1\le q\le 2\cdot 10^5\)。
时间限制 \(\text{8000ms}\),空间限制 \(\text{512MB}\)。
Solution
考虑按照时间根号分治,我们将连续 \(B\) 个操作一起处理。
我们将操作到的点(即 \(2\) 操作的 \(x\) 和 \(3\) 操作的 \(x,y\))染黑,只有这些黑点是进行操作的。
考虑操作前的每个置换环,它形如这样:
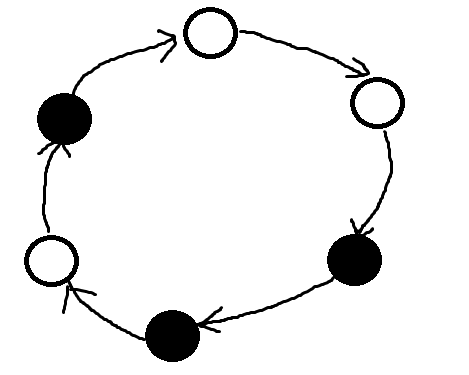
我们将其划分成若干条“链”(红色区域),可以发现操作中每条链都是以整体出现的,即 \(\Delta\) 相等:
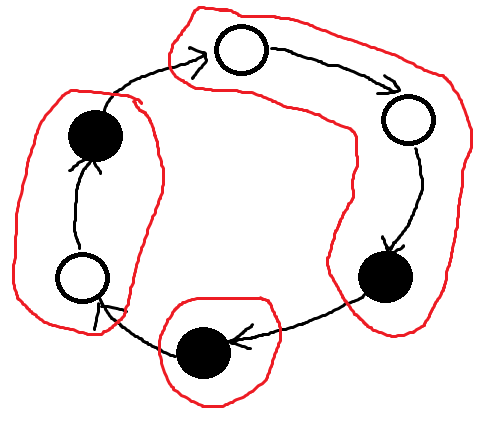
而链只有 \(2B\) 个,因此我们只需要对每个链维护 \(\Delta\) 即可。
对于 \(1\) 操作,区间 \([l,r]\) 的点权和即为操作前的 \(\sum\limits_{i=l}^{r}a_i\) 再加上 \(\sum\limits_{每条链}\Delta \times 环内编号在[l,r]的点数\),复杂度 \(O(B\log n)\)。
对于 \(2\) 操作,它必然是给当前 \(x\) 所在的链,以及这条链所在的环的其他链,增加 \(y\),复杂度 \(O(B)\);
对于 \(3\) 操作,我们交换两个黑点连到的链编号,是 \(O(1)\) 的。
至此,我们可以在 \(O(\frac{q}{B}\cdot (B^2\log n+n))\) 复杂度解决。
取 \(B=\sqrt{n/\log n}\),时间复杂度 \(O(q\sqrt{n\log n})\)。

