CodeForces-EDU-105 Div2 部分题解报告
EDU 105 Div2 部分题解报告
要加油奥!(ง •_•)ง
A. ABC String
原题链接:传送门
考点:思维,暴力枚举
题目大意
给你一个字符串,字符串只包含三种字符:'A','B','C',你可以将这个字符串中的任意一类字符
全部替换成某一类括号例如
AAA ---> ((( 或者 BBB ---> )))
现在问你如何进行替换可以替换后的字符串括号匹配,如果存在一种情况可以满足输出 YES 否则输出NO.
分析
通过观察我们可以发现,数据的范围比较小字符串的长度范围为\([2,50]\),我们可以采用暴力的方式去做
我们可以一次枚举每一个字符当前的类型。然后再进行一遍括号匹配检查
如果你之前不知道检查括号是否匹配的方法 建议看学习一下括号匹配算法并背下来(懂了嘛
AC code
外面三层循环枚举了 A B C 被哪一类括号替换
最内层循环 检查当前替换后的括号是否合法
void slove()
{
string s;cin >> s;
string str = "()";
for(int a = 0; a < 2; a ++)
{
for(int b = 0; b < 2; b ++)
{
for(int c = 0; c < 2; c++)
{
int res = 0;
for(int i = 0; i < s.size(); i ++)
{
if(s[i] == 'A')
{
if(!a)res ++;
else res --;
}
if(s[i] == 'B')
{
if(!b) res ++;
else res --;
}
if(s[i] == 'C')
{
if(!c) res ++;
else res --;
}
if(res < 0)break;
}
if(res == 0)
{
cout << "YES" << endl;
return;
}
}
}
}
cout << "NO" << endl;
}
B. Berland Crossword
原题链接:传送门
考点 :思维,暴力,贪心
分析
- 首先通过观察数据范围可以数据范围较小可以使用暴力
通过观察我们可以知道,实际上会出现矛盾的情况取决于四个角的情况。
这四个角只可能存在两种情况:
- 被染成黑色
- 保持白色
所以我们依次去枚举四个角的使用情况
我们使用 0 表示这个角未被使用, 1 表示这个角已经被使用。
for(int aa = 0; aa < 2; aa ++) // 左上角
{
for(int bb = 0; bb < 2; bb ++) // 右上角
{
for(int cc = 0; cc < 2; cc ++) // 左下角
{
for(int dd = 0; dd < 2; dd ++) // 右下角
{
// 检查是否合法
}
}
}
}
枚举了四个角的情况之后我们只需要考虑什么情况下会产生冲突
此处拿第一列来举例
例如在一个 3 * 3 的正方形中
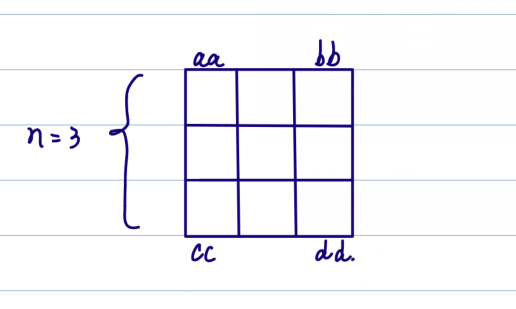
冲突情况 1 :
当给定 \(l < aa + bb\) 时,此时我们要求的是第一列一共需要 l 个黑色的方块,但是此时aa 位置 和 bb 位置的黑色块数已经大于 l 了 那么此时一定矛盾。
如果假设我们给定的 \(l = 1\), 如果此时 aa 和 bb 已经被占用 那么会发生冲突故此种情况淘汰。
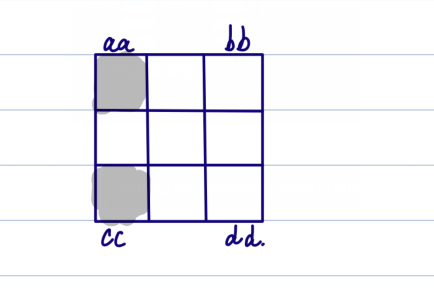
冲突情况2
当排除掉两个角之后剩下的位置 + 两个角所占用的位置的黑色个数 < l
\(n - 2 + aa + cc < l\)
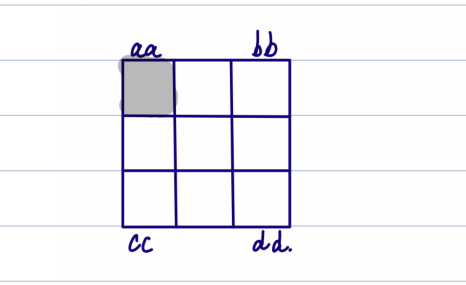
假设我们当前 aa , cc 的位置的占用情况如上图所示,此时我们要求 l = 3,那么 会产生冲突故当前情况 pass.
综上我们只需要枚举出来四个角的情况,并且每一次根据两个角的情况来判断该行或者该列的情况是否符合以上两种矛盾的情况如果符合那么就跳过该种情况。如果都通过那么此时这种布局为正确。否则为NO
AC代码
void slove()
{
int n, u, r, d, l;
cin >> n >> u >> r >> d >> l;
for(int aa = 0; aa < 2; aa ++) // 第一个角
{
for(int bb = 0; bb < 2; bb ++) // 第二个
{
for(int cc = 0; cc < 2; cc ++) // 第三个
{
for(int dd = 0; dd < 2; dd ++) // 第四个
{
if(aa + cc > l || n - 2 + aa + cc < l)
continue;
if(bb + dd > r || n - 2 + dd + bb < r)
continue;
if(aa + bb > u || n - 2 + aa + bb < u)
continue;
if(cc + dd > d || n - 2 + cc + dd < d)
continue;
// 以上的矛盾都不满足那么此时这种布局一定正确
cout << "YES" << endl;
return;
}
}
}
}
cout << "NO" << endl;
}


