图论 - 二分图的判断(dfs染色法)

二分图的判断(dfs染色法)

如何判断一个图是否为二分图
普通染色法模板
C++ 代码模板如下

思想:先将当前点染色，然后再将该点相连的结点进行染另外一种颜色
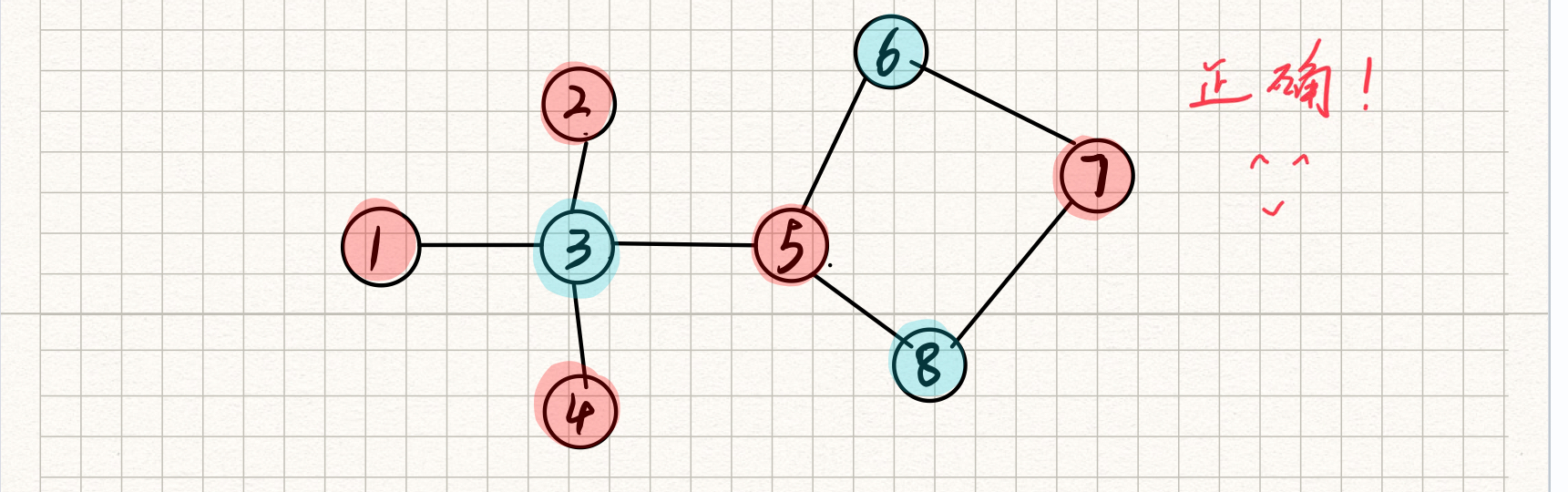
下面附上自己画的一张图假设我们从第一个点开始染成红色
后面的染色过程结合下面的代码就很好理解啦

宝图奉上: 请结合代码分析效果会更好
正确情乱:

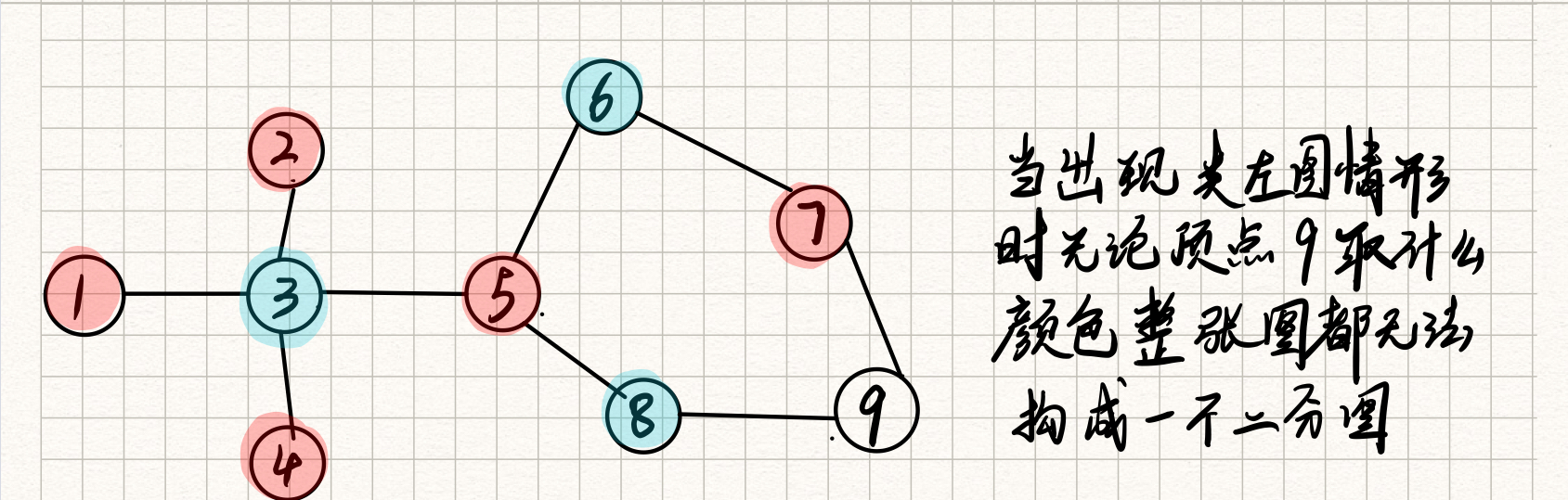
无法构成二分图的例子如下:

染色过程核心代码

bool dfs(int node, int col)
{
	color[node] = col; //染色
	for (int i = 0; i < G[node].size(); i++)
	{
		//如果相邻的顶点同色，就剪掉这一枝，返回false
		if (color[G[node][i]] == col)return false;
		if (color[G[node][i]] == 0 && !dfs(G[node][i],-col))return false;
	}
	//如果都染了色返回true
	return true;
}

整体代码

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;
const int inf = 1000;
int V, E;
vector<int> G[inf];
int color[inf] = {0};
bool dfs(int node, int col)
{
	color[node] = col; //染色
	for (int i = 0; i < G[node].size(); i++)
	{
		//如果相邻的顶点同色，就剪掉这一枝，返回false
		if (color[G[node][i]] == col)return false;
		if (color[G[node][i]] == 0 && !dfs(G[node][i],-col))return false;
	}
	//如果都染了色返回true
	return true;
}
void dfsTrave()
{
	for (int i = 0; i < V; i++)
	{
		if (color[i] == 0)
		{
			if (!dfs(i, 1))
			{
				cout << "No" << endl;
				return;
			}
		}
	}
	cout << "Yes" << endl;
}
int main()
{
	cin >> V >> E;
	int a, b;
	for (int i = 0; i < E; i++)
	{
		cin >> a >> b;
		G[a].push_back(b);
		G[b].push_back(a);
	}
	dfsTrave();
	system("pause");
	return 0;
}

如果大家有什么疑问的话可以加qq向我提出哦,欢迎各位大佬指出问题。
如果你觉得对你有所帮助的话就给我点个赞,点燃我下次写文章的动力吧 ^_ !