1035. 不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

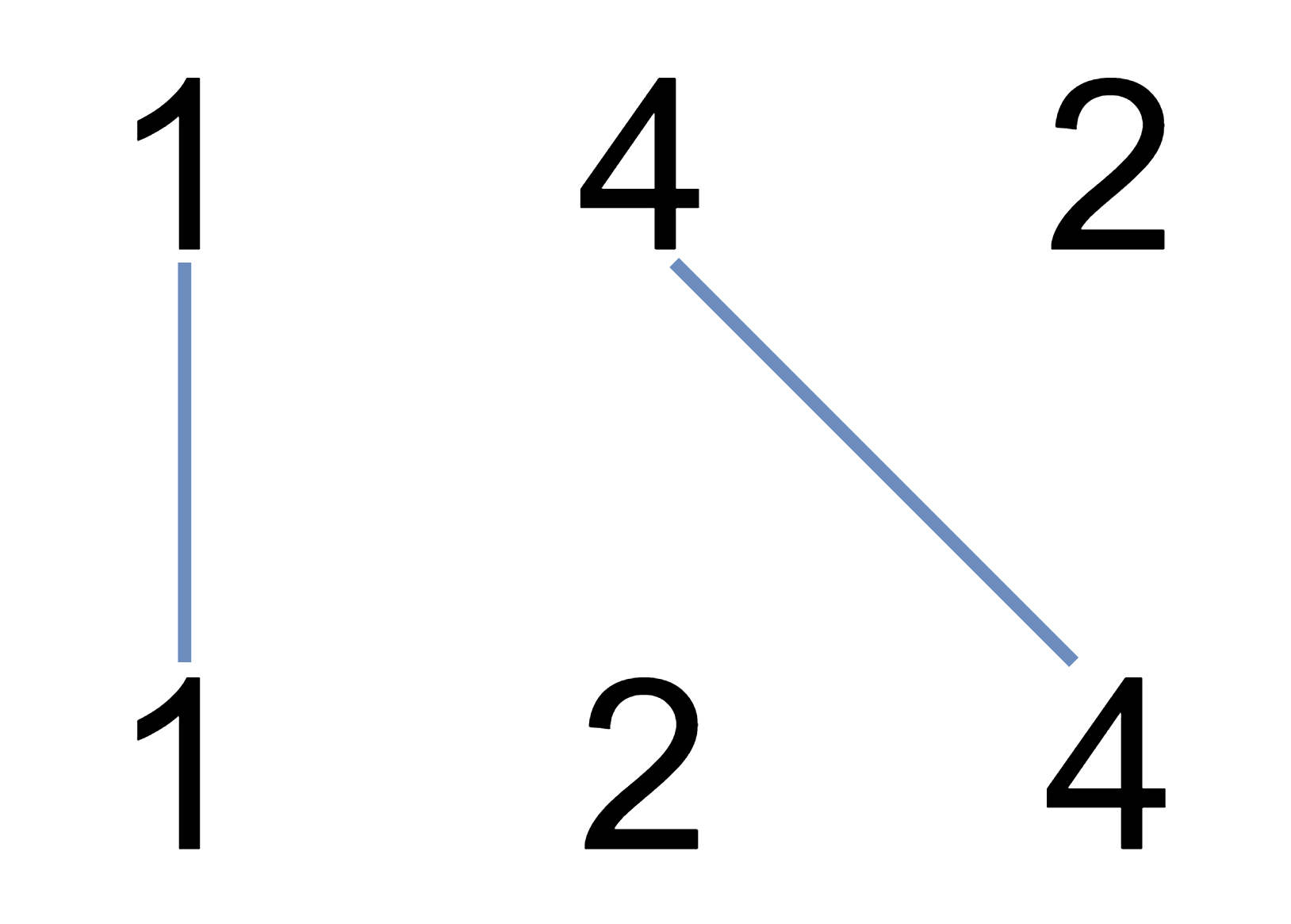
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000

解题思路

题目中要求绘制的直线要满足两个条件，一是nums1[i] == nums2[j]，二是绘制的直线不与任何其他连线（非水平线）相交。

直线不能相交，这就是说明在nums1中找到一个与nums2相同的子序列，并且这个子序列不能改变相对顺序，如果改变了相对顺序，那链接相同数字的直线就会相交。

也就是说本题其实就是1143. 最长公共子序列换了一种说法而已，就是在求两个数组的最长公共子序列。

C++

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
                }
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

JavaScript

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var maxUncrossedLines = function(nums1, nums2) {
    const dp = Array(nums1.length + 1).fill().map(item => Array(nums2.length + 1).fill(0));
    for (let i = 1; i <= nums1.length; i++) {
        for (let j = 1; j <= nums2.length; j++) {
            if (nums1[i - 1] === nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
            }
        }
    }
    return dp[nums1.length][nums2.length];
};