63. 不同路径 II

63. 不同路径 II

题目链接： 63. 不同路径 II(中等)

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

• m == obstacleGrid.length

• n == obstacleGrid[i].length

• 1 <= m, n <= 100

• obstacleGrid[i][j] 为 0 或 1

解题思路

与62. 不同路径类似，都可以采用动态规划解决。

1. 确定dp数组以及其下标的含义

   该题的dp数组是一个二维数组。dp[i,j]表示从(0,0)出发到(i,j)的路径数

2. 确定递推公式

   题目中表示每一步只能向下或向右移动，所以要走到 (i,j)处，只能从从(i,j-1)处向下走一步或从(i-1,j)处向右走一步。所以可以得到递推公式： dp[i,j] = dp[i,j - 1] + dp[i - 1,j]。但是需要注意，如果 (i,j)处有障碍，那dp[i,j] = 0。

3. dp数组的初始化

   从(0, 0)到(i, 0)的路径只有一条，所以dp[i,0] = 1，但如果(i, 0)处有障碍，那(i, 0)及后面的初始值都为0(如下图所示)，dp[0,j]同理。

   

4. 确定遍历顺序

   由递推公式可以看出dp[i,j]是由其上方和其左方推到出来的，所以遍历顺序是从左到右一层一层地遍历的

5. 举例推导dp数组

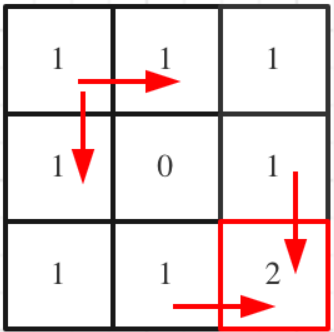
   在例1中，可以得到的dp数组如下所示

    

C++

class Solution {
public:
    // 将obstacleGrid数组直接转为dp数组
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        for (int i = 0; i < m; i++) {
            if (obstacleGrid[i][0] == 0) { //表示当前位置无障碍
                if (i > 0 && obstacleGrid[i - 1][0] == 0) { //表示当前位置的左边有障碍(已经从1变为了0)
                    obstacleGrid[i][0] = 0;
                }
                else obstacleGrid[i][0] = 1;
            }
            else if (obstacleGrid[i][0] == 1) { //表示当前位置有障碍
                obstacleGrid[i][0] = 0;
            }
        }
        for (int j = 1; j < n; j++) {
            if (obstacleGrid[0][j] == 0) { //表示当前位置无障碍
                if (j > 0 && obstacleGrid[0][j - 1] == 0) { //表示当前位置的左边有障碍(已经从1变为了0)
                    obstacleGrid[0][j] = 0;
                }
                else obstacleGrid[0][j] = 1;
            }
            else if (obstacleGrid[0][j] == 1) { //表示当前位置有障碍
                obstacleGrid[0][j] = 0;
            }
        }
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                if(obstacleGrid[i][j] == 1) obstacleGrid[i][j] = 0;
                else obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
            }
        }
        return obstacleGrid[m - 1][n - 1];
    }
};
​
class Solution1 {
public:
    // 重新定义dp数组并全部初始化为0
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) continue;
                else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

JavaScript

/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function(obstacleGrid) {
    let m = obstacleGrid.length;
    let n = obstacleGrid[0].length;
    const dp = Array(m).fill().map(item => Array(n).fill(0));
​
    for (let i = 0; i < m && obstacleGrid[i][0] === 0; i++) dp[i][0] = 1;
    for (let j = 0; j < n && obstacleGrid[0][j] === 0; j++) dp[0][j] = 1;
​
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            if (obstacleGrid[i][j] === 1) continue;
            else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
​
    return dp[m - 1][n - 1];
};

时间复杂度：O(m × n)

空间复杂度：O(m × n)