376. 摆动序列

376. 摆动序列

题目链接：376. 摆动序列(中等)

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2 

提示：

• 1 <= nums.length <= 1000

• 0 <= nums[i] <= 1000

进阶：你能否用 O(n) 时间复杂度完成此题?

解题思路

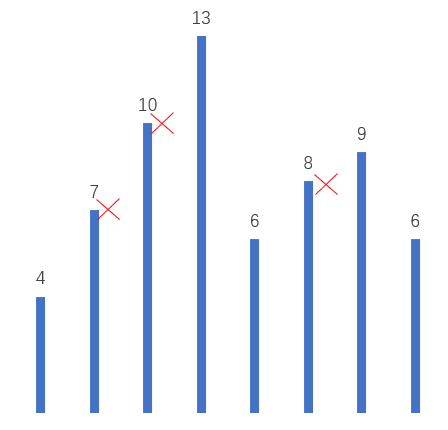
结合下图及题目的要求，我们需要将单调坡度上的中间元素全部删除(操作时并不需要真的去删除，我们只需要统计元素个数即可)，保证每个坡度只有两端的元素即可得到最长摆动序列。该题也是用到了贪心算法的思想，局部最优：删除单调坡度的中间节点，整体最优：整个序列有最多的坡度，从而得到最长摆动序列。

C++

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        // 如果数组中只有一个元素时，也是摆动序列，此时的最长子序列长度就是 1
        if (nums.size() <= 1) return nums.size();
        int pre = 0; // 记录前一对的差值
        int cur = 0; // 记录后一对的差值
        int result = 1; // 记录摆动序列 的 最长子序列的长度，此时数组中的元素个数是大于等于2的，所以需要将坡度开头的那个元素算进去
        for (int i = 0; i < nums.size() - 1; i++) {
            cur = nums[i + 1] -nums[i];
            if (pre >= 0 && cur < 0 || pre <= 0 && cur > 0) {
                result++;
                pre = cur;
            }
        }
        return result;
    }
};

JavaScript

var wiggleMaxLength = function(nums) {
    if (nums.length <= 1) return nums.length;
    let pre = 0;
    let cur = 0;
    let result = 1;
    for (let i = 0; i < nums.length - 1; i++) {
        cur = nums[i + 1] - nums[i];
        if (pre >= 0 && cur < 0 || pre <= 0 && cur > 0) {
            result++;
            pre = cur;
        }
    }
    return result;
};