40. 组合总和 II

40. 组合总和 II

题目链接：40. 组合总和 II(中等)

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100

• 1 <= candidates[i] <= 50

• 1 <= target <= 30

解题思路

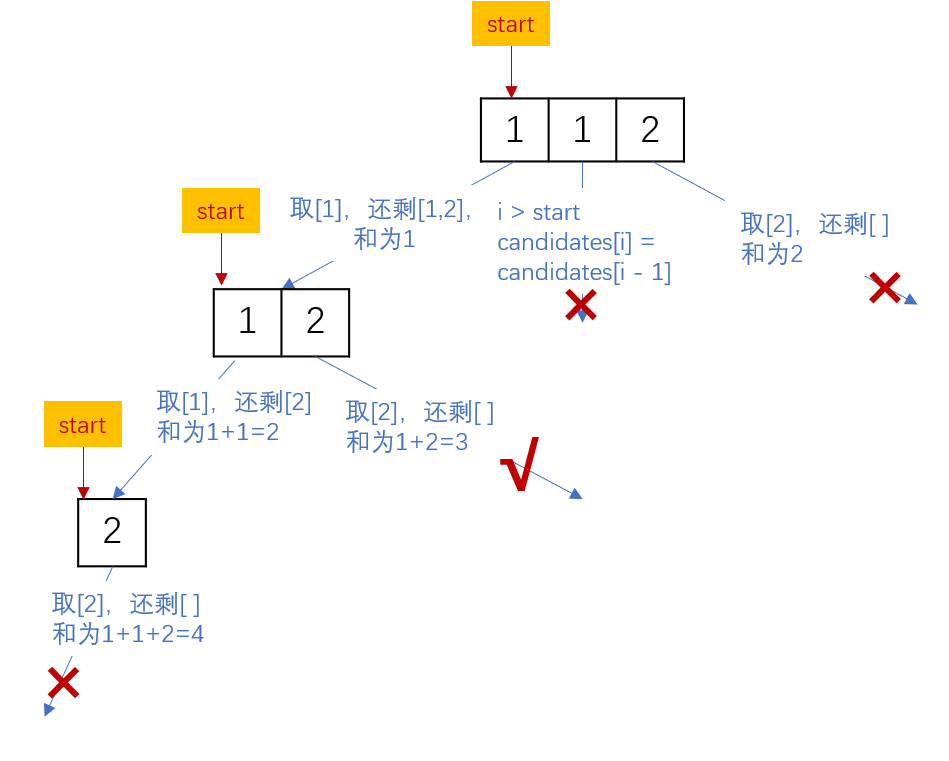
下图所示是排序好的数组candidates = [1，1，2]，target = 3。本题需要注意的一点是，需要对树的同一层进行去重，而不同层的不需去重。即横向去重，纵向不去重。从图来看，每一层的数组都是以start所指元素为首，所以在同一层如果有i > start && candidates[i] ==candidates[i - 1]，那么就需要进行去重。

C++

class Solution {
public:
    vector<int> path;
    vector<vector<int>> result;
    void backTracking(vector<int> candidates, int target, int start, int sum) {
        if (target == sum) {
            result.push_back(path);
            return;
        }
        for (int i = start; i < candidates.size(); i++) {
            // 去重 精髓在于 i > start
            if (i > start && candidates[i] == candidates[i - 1]) continue;
            // 剪枝
            if (sum + candidates[i] > target) continue;
            path.push_back(candidates[i]);
            sum += candidates[i];
            backTracking(candidates, target, i + 1, sum);
            path.pop_back();
            sum -= candidates[i];
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        path.clear();
        result.clear();
        sort(candidates.begin(), candidates.end()); // 排序，从小到大
        backTracking(candidates, target, 0, 0);
        return result;
    }
};

JavaScript

let path = [];
let result = [];
​
const compare = (x, y) => { //比较函数
    if (x < y) {
        return -1;
    } else if (x > y) {
        return 1;
    } else {
        return 0;
    }
}
​
const backTracking = (candidates, target, start, sum) => {
    if (sum === target) {
        result.push([...path]);
        return;
    }
    for (let i = start; i < candidates.length; i++) {
        if (i > start && candidates[i] === candidates[i - 1]) continue;
        if (sum + candidates[i] > target) continue;
        path.push(candidates[i]);
        sum += candidates[i];
        backTracking(candidates, target, i + 1, sum);
        path.pop();
        sum -= candidates[i];
    }
}
​
var combinationSum2 = function(candidates, target) {
    path = [];
    result = [];
    candidates.sort(compare);
    backTracking(candidates, target, 0, 0);
    return result;
};